油膜覆蓋的非線性海面電磁散射多普勒譜特性研究?

王蕊 郭立新 張策

(西安電子科技大學物理與光電工程學院,西安 710071)

(2018年1月25日收到;2018年9月27日收到修改稿)

1 引 言

實際的海洋表面是一個時刻動態變化的復雜環境,其上漂浮著不同起源的油膜[1,2],包括人工來源,如人類在石油開采、運輸過程中的溢油事故所產生的海面浮油,以及由海洋生物活動所產的有機天然油膜來源.海洋環境的復雜性以及油膜種類的多樣性決定了海洋油膜污染的監測以及油膜種類辨別是一項具有很大挑戰性的工作.目前,大量的海面雷達后向回波測量實驗證實,海面油膜對雷達回波的后向散射系數具有明顯的影響.但海面雷達回波的平均散射系數只能反映雷達回波強度的均值分布水平,而實際的海洋環境時刻處于復雜多變的運動之中,因而雷達回波的多普勒譜是一個更加精確和有效的監測波浪運動的工具.國外多普勒雷達海面回波實驗[3?5]結果證實,有油膜覆蓋的海面其散射回波的多普勒頻移與干凈海面散射回波的多普勒頻移具有明顯差異,這說明海面上覆蓋有油膜時對雷達散射回波的多普勒特性具有顯著的影響.海面散射回波的多普勒特性在探測油膜方面的優勢預示著多普勒雷達在監測及分辨不同種類油膜方面具有潛在的應用價值.這啟發我們可以從油膜與海面相互作用的電磁散射機理角度出發,借助仿真算法,去研究油污海面的多普勒特性,為利用雷達回波多普勒特性進行海洋油膜探測提供一定的物理理論基礎.

近年來,國內外學者開始關注有油膜覆蓋的海面電磁散射特性,所涉及的電磁散射算法也主要分為高頻近似[6,7]以及嚴格的數值算法[8,9].文獻[10]將油膜覆蓋的海面近似為單層粗糙面模型,利用小斜率近似方法建立了海洋上方附著極薄生物膜的散射模型.意大利學者Nunziata等[11]基于雙尺度模型研究了單分子層油膜對海面雷達散射系數的影響,并與合成孔徑雷達獲得的實測數據進行了對比.從電磁散射角度看,有油膜覆蓋的海面電磁仿真模型應該歸結為分層粗糙海面散射模型.法國學者Pinel等[12,13]基于考慮多次散射的近似電磁模型研究了油膜覆蓋的線性海面電磁散射特性;Ghanmi等[14]基于前后向迭代(FBM)研究了不同頻段(C,X,Ku)下油膜覆蓋海面的電磁散射建模.以上學者大多針對線性海面進行仿真,盡管線性海面在一定范圍內可以較合理地描述海浪的運動規律,但基于線性海面模型預測的海面電磁散射特性尤其是海面雷達回波的多普勒特性和實測數據存在較大差異[15?17].為了更好地研究油膜覆蓋海面的散射回波特性,本文以Creamer非線性模型為基礎,研究油膜覆蓋的一維非線性分層海面散射回波的多普勒譜特性.油膜覆蓋海面的電磁散射可歸于分層粗糙面散射建模問題,就分層粗糙面的電磁散射建模而言,目前仍主要分為兩大類方法:一類方法為高頻近似方法,如基于廣義反射系數的物理光學方法;另一類為經典數值方法,如矩量法、時域有限差分方法等.迭代物理光學方法既彌補了傳統高頻算法計算精度低的缺陷又避免了經典數值算法計算效率低的弊端.因此本文采用迭代物理光學法研究油膜覆蓋的一維非線性分層海面散射回波的多普勒譜特性,比較和分析了線性與非線性、干凈海面與油膜覆蓋海面的多普勒譜特征之間的差異.與經典數值算法相比,本文所采用的迭代物理光學方法計算效率較高,與傳統的高頻方法相比,精度又有所保障.數值結果重點討論了入射角、油膜參數以及海面風速對Creamer非線性海面的雷達散射回波多普勒譜展寬和頻移的影響.

2 油膜覆蓋的非線性海面幾何建模

當海面上覆蓋油膜時,油膜的黏滯性會對海浪波產生阻尼作用,尤其對于海浪波中的毛細波成分造成一定的破壞作用.Lombardini等[18,19]對該阻尼作用進行了廣泛的研究,認為這是一種油膜引起的諧振類的阻尼作用,該阻尼作用可用馬朗戈尼(Marangoni)波和拉普拉斯波的耦合理論來解釋.根據該理論,當油膜參數確定后,可通過計算油膜阻尼率[19],結合現有的海面功率譜密度函數計算得到油膜覆蓋海面時對應的功率譜密度函數.

本文模擬干凈海面的功率譜密度函數采用PM海譜[20],具體表達式為

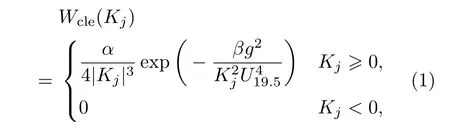
其中α =8.10×10?3,β =0.74,U19.5為海面上方19.5 m高度處的風速,g為重力加速度,Kj=2πj/L.根據文獻[19]的分析,油膜覆蓋海面的功率譜密度函數Wcon(Kj)可表示為

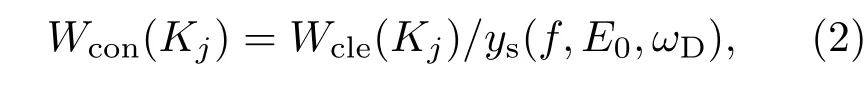
其中油膜阻尼率ys可表示為

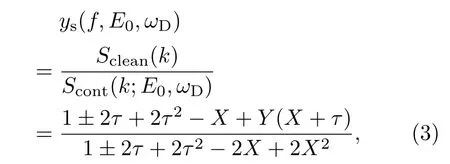
其中

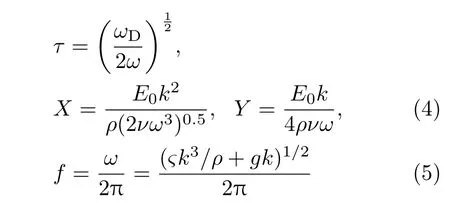
為色散關系.在(3)式中“+”代表可溶解的油膜,而“?”代表不可溶解的油膜.本文的數值結果取“?”.g0為重力加速度,ρ是海水密度,ν=10?6m/s為黏性系數,?=74×10?3N/m為表面張力,E0為彈性模量,ωD依賴于分子力之間的結構弛豫.

圖1 干凈海面與受污海面的海譜比較Fig.1.Comparison of the spectra between clean and contaminated ocean.

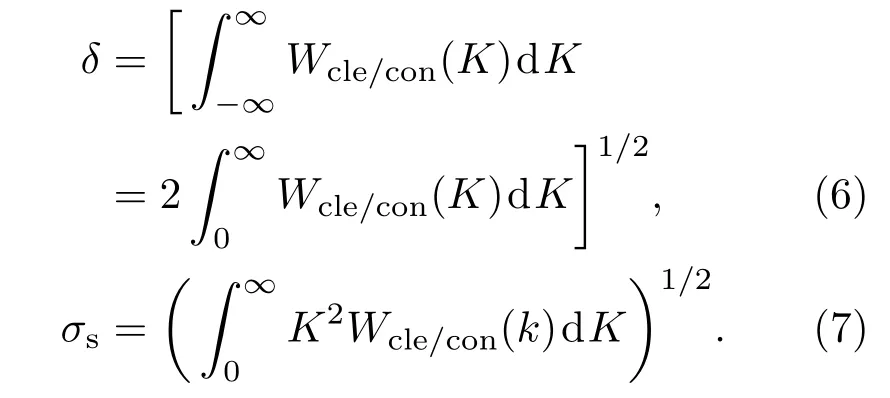
從圖2和圖3可以清楚地看到,當海面上方覆蓋油膜時,由于油膜的黏滯阻尼作用在一定程度上破壞了海浪波中的毛細波成分,所以受污海面的均方根高度及斜率相較干凈海面(粗實線)均有所降低.

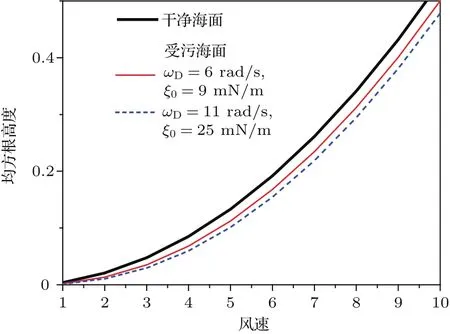
圖2 干凈海面與受污海面的均方根高度比較Fig.2.Root-mean-squared height of clean and contaminated ocean.

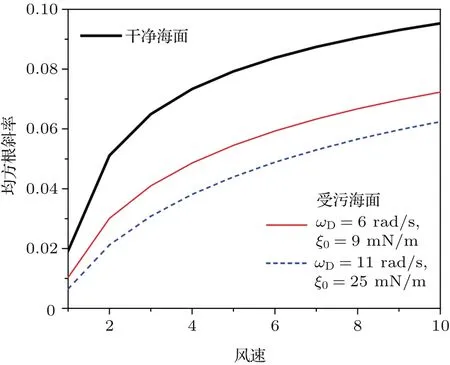
圖3 不同風速下的海面均方根斜率Fig.3.Root-mean-squared slope of clean and contaminated ocean.

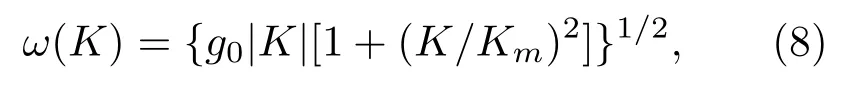
在得到油膜覆蓋海面的海譜后,簡單介紹Creamer非線性時變海面建模方法.線性海面生成中把海面高度起伏看作多個振幅為高斯分布的獨立諧波疊加而成,每個諧波的傳播頻率和空間波數滿足以下色散關系:g0=9.81 m/s2為重力加速度,Km與海水張力T以及密度ρ有關,Km=(ρg0/T)0.5.線性海面可通過對(1)和(2)式進行逆傅里葉變換實現.任意時刻t頻域表示的傅里葉變換分量可以表示為

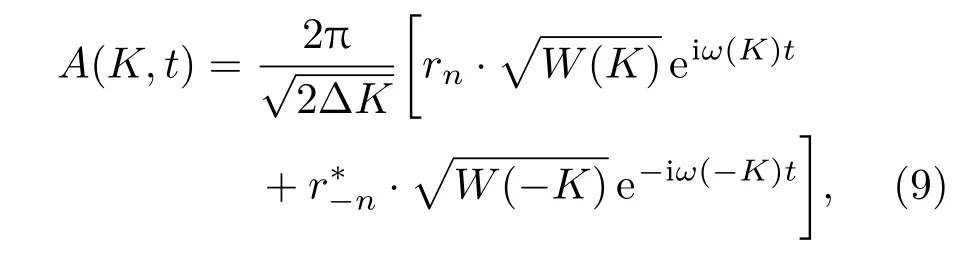
這里W(K)即(1)和(2)式的海譜形式;rn為符合標準正態分布的復高斯隨機序列,r??n為其逆序共軛;?K=2π/L,L為海面長度.對(9)式進行逆傅里葉變換可生成線性海面,

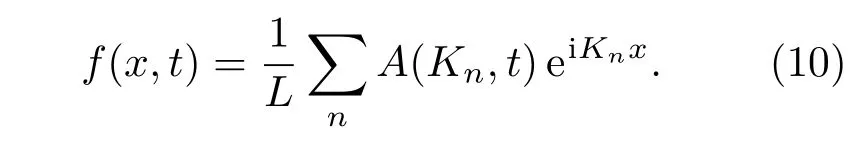
對(10)式得到的線性海浪進行希爾伯特變換[21],

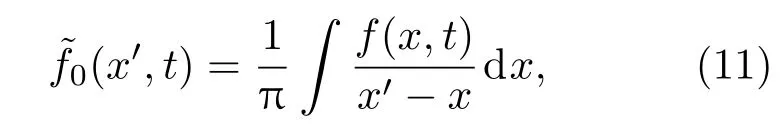
則Creamer非線性海浪頻域表示的傅里葉變換分量可由下式得到:

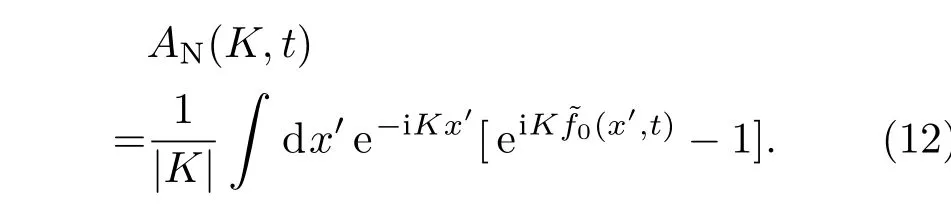
對上式進行逆傅里葉變換即可得到非線性海面的高度起伏.圖4給出了風速為3 m/s時的一維Creamer非線性海面的幾何輪廓,共三條曲線,其中粗實線表示基于Wcle(Kj)模擬的干凈海面幾何輪廓,其他兩條曲線表示基于Wcon(Kj)模擬的油膜覆蓋海面的幾何輪廓.從海面幾何輪廓對比結果可以更直觀地看到油膜的存在對于海浪波輪廓的影響.油膜參數越大(虛線),其阻尼作用越強,對海面輪廓的修正也越發明顯.

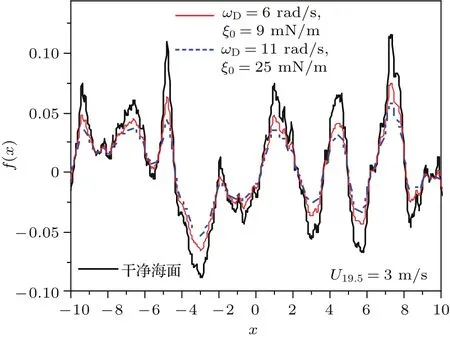
圖4 干凈海面與受污海面表面輪廓Fig.4.Comparison of the surface height profile between clean and contaminated ocean.

3 油膜覆蓋海面散射回波的多普勒譜建模

鑒于油膜覆蓋海面的散射模型可視為分層粗糙海面模型,現已有諸多電磁仿真方法用于分析油膜覆蓋海面的單、雙站散射特性[11?14],鮮有文獻研究其后向散射回波特性,尤其是基于非線性模型的油膜覆蓋海面后向散射回波特性.在上述建立的Creamer非線性海面幾何模型的基礎上,本節采用迭代物理光學方法[22]建立其后向散射回波的多普勒譜模型[23?25].迭代物理光學方法[22]的主要思想過程如下.當入射波照射到油膜層產生極化電磁流Js0(ρ0),Ms0(ρ0),由邊界條件可得到其下方的極化電磁流Ju0,Mu0.迭代物理光學法認為海面上任意一點處的電磁流是由整個油膜下邊界的Ju0,Mu0的輻射場Ed1(ρ1)=Le(Mu0,Ju0);Hd1(ρ1)=Lh(Mu0,Ju0)所激發,如圖5所示.

圖5 海面散射場Ed1,Hd1計算策略示意圖Fig.5.Geometry for the contribution of the scattered if eld Ed1,Hd1.

在得到Ed1(ρ1),Hd1(ρ1)后由物理光學方法可計算得到海面上方的電磁流:

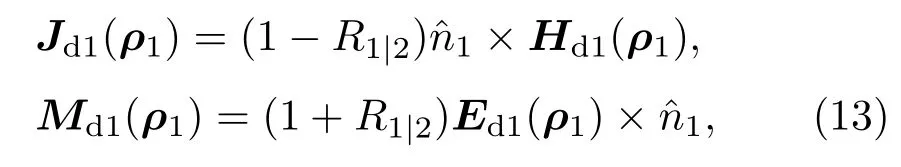
其中R1|2為油膜到海面層的反射系數. 同理,油膜層任意點處的電磁流也是由整個海面層電磁流Jd1,Md1的輻射場共同決定,Eu1(ρ0)=Le(Md1,Jd1);Hu1(ρ1)=Lh(Md1,Jd1), 由物理光學方法可得到Ju1,Mu1.再由邊界條件得到Js1,Ms1,如此即完成了一次迭代.依次迭代下去直至滿足誤差要求即停止迭代,結束迭代后總電磁流可表示為

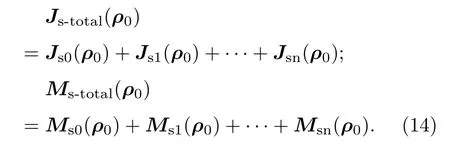
為了驗證所采用的迭代物理光學方法的有效性,圖6給出了迭代物理光學方法與矩量法計算油膜覆蓋海面的結果比較.從圖6的仿真曲線可以看出,絕大數散射角范圍內,迭代物理光學方法與矩量法仿真結果符合的較好,從而驗證了本文所采用的迭代物理光學方法的正確性.為了比較兩種方法的計算效率,表1給出了圖6仿真結果對應的計算機內存和計算時間的比較.其中計算機處理器主頻為2.3 GHz,內存為3.47 GB.從表1可以看出,本文所采用的迭代物理光學方法所需要的計算機內存僅是矩量法的0.128%,計算耗時為矩量法的1.75%.這也正是本文采用迭代物理光學方法的原因.

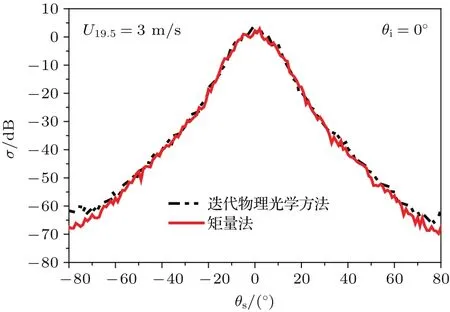
圖6 迭代物理光學方法與矩量法計算油膜覆蓋海面的散射結果對比Fig.6.Comparison of numerical results of contaminated sea obtained by our method and MoM.

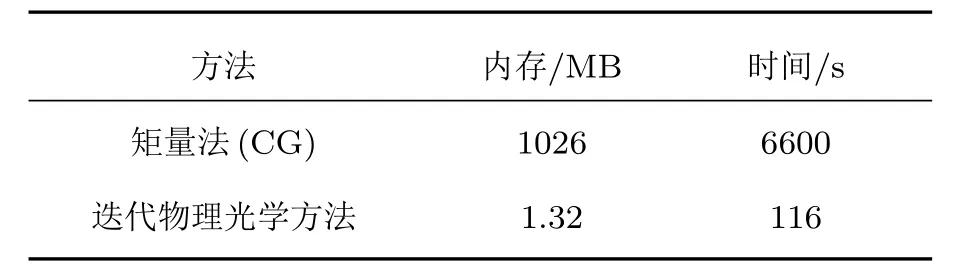
表1 單個海面樣本的計算機內存及計算時間比較Table 1.Comparison of computer resource for one realization.

海面散射回波的多普勒譜通常定義為散射場時間自相關函數傅里葉變換,即

第一步,設定時間間隔τ,仿真一組連續的時變油膜覆蓋海面的樣本.對于連續的電磁波入射,當τ足夠小,可認為在該時間間隔內,海面是“靜止的”.

第二步,對每一個“靜止的”海面樣本,采用迭代物理光學方法求得其后向散射場.

第三步,利用(13)式計算油膜覆蓋海面的散射回波信號的多普勒譜.

第四步,重復前三個步驟,得到多組雜波譜計算結果并求集平均.

為了定量地衡量多普勒譜,可以通過考察其關于頻率的一階矩和二階矩,即多普勒頻移和展寬.多普勒頻移通常定義為

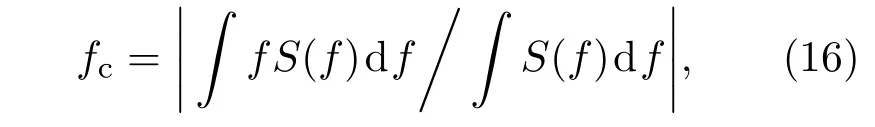
多普勒頻移fc與功率加權的散射體的平均的雷達視向速度有關.多普勒譜展寬是由散射面元相對于的雷達視線方向的速度的方差決定.由于海面各部分的雷達視線速度并不相同,并且有的面元向接近雷達視線運動,有的面元背離雷達視線運動,從而時變海面的雷達回波的多普勒譜并不是單一的譜線,而是具有一定譜寬度的連續的頻譜密度函數,譜寬定義為

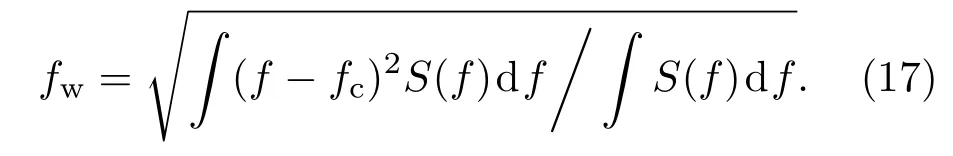
在本文多普勒譜仿真計算中,時間間隔取0.02 s對海面進行離散[25],每一組多普勒譜由256個連續的后向散射樣本計算得到,對50組譜曲線求平均作為最終的結果.入射波頻率是1 GHz,海水溫度為10?C,鹽度為1.5%,相對介電常數為(74.0,61.0),油膜的介電參數為(2.2,0.005),油膜厚度為5 mm.極化方式為水平極化.海面長度[26]為L=153.6 m,錐形波因子[26]為L/4.

為了便于多普勒譜頻移和譜寬的對比分析,以下算例中的多普勒譜曲線均用其各自的最大值進行了歸一化處理.圖7給出了線性與Creamer非線性海面歸一化多普勒譜結果的比較,其中每幅圖中的兩條曲線均分別代表干凈海面以及油膜覆蓋海面的多普勒譜結果.同時圖中還給出了布拉格頻移的理論結果[23,24],其中,受污海面上漂浮的油膜參數為{ξ0=25 mN/m,ωD=11 rad/s},海面風速為3 m/s.從圖中可以看出,在小入射角下,基于線性模型與Creamer非線性模型的干凈海面的多普勒譜幾乎沒有差異,并且線性海面的多普勒譜頻移均大于布拉格頻移,這說明線性海面電磁散射貢獻在小角度情形下只要來自于鏡面反射.隨著入射角的增大,線性海面的多普勒譜幾乎收縮為一根線,并且和布拉格線重合,因為在大入射角下,布拉格散射在線性海面的電磁散射中占據主導地位.而此時線性與Creamer非線性海面的多普勒譜差異越來越明顯.具體而言,在中等和大入射角下,Creamer非線性海面的多普勒譜的譜寬基本保持不變,并無明顯減小的趨勢,這與線性海面多普勒譜的譜寬變化明顯不同,這種差異主要是因為隨著入射角的增大,非線性波浪的運動速度要大于線性波浪,所以譜寬相對于后者要大一些,尤其在接近掠入射情形.此外,隨著入射角的增大,相同入射角下,Creamer非線性海面的多普勒頻移總大于線性海面的多普勒頻移.本文研究的是一維海面情形,其散射回波的多普勒譜難以定量地用二維實測數據檢驗,但就Creamer非線性海面的多普勒頻移和展寬所表現出的特性與文獻[27]實測結果得到的定性規律相符合,這亦能從一定程度上說明Creamer非線性海面相較線性海面的優勢所在.

當海面漂浮油膜時,海面多普勒譜的變化也出現了類似的規律.為了更好地說明該規律,圖8給出了線性和Creamer非線性海面的多普勒譜頻移和展寬隨入射角的變化規律.從圖8中可以發現,在小入射角下,油膜覆蓋的線性海面與Creamer非線性海面的多普勒譜頻移及展寬均無明顯差異.隨著入射角的增大,在相同入射角下,油膜覆蓋的Creamer非線性海面多普勒頻的譜寬明顯比線性海面多普勒頻譜的譜寬要寬且多普勒頻移總大于線性海面的多普勒頻移.

圖7和圖8說明仿真計算得到的大入射下線性海面散射回波的多普勒譜幾乎收縮為以布拉格頻移為中心的極窄的譜線,這與海洋多普勒雷達測量結果給出的規律并不一致.在一系列理論研究和對實測數據分析的基礎上,人們認為海浪波之間應該具有非常復雜的非線性相互作用,而線性海面只是具有不同權重的一系列沿不同方向傳播的不同頻率的諧波的線性組合,它忽略了海浪波之間的非線性相互作用.因而在掠入射情形下,線性海面散射回波的多普勒不可避免地表現出不符合實際的行為.這也是本文采用Creamer非線性模型建立油膜覆蓋海面幾何模型的初衷.

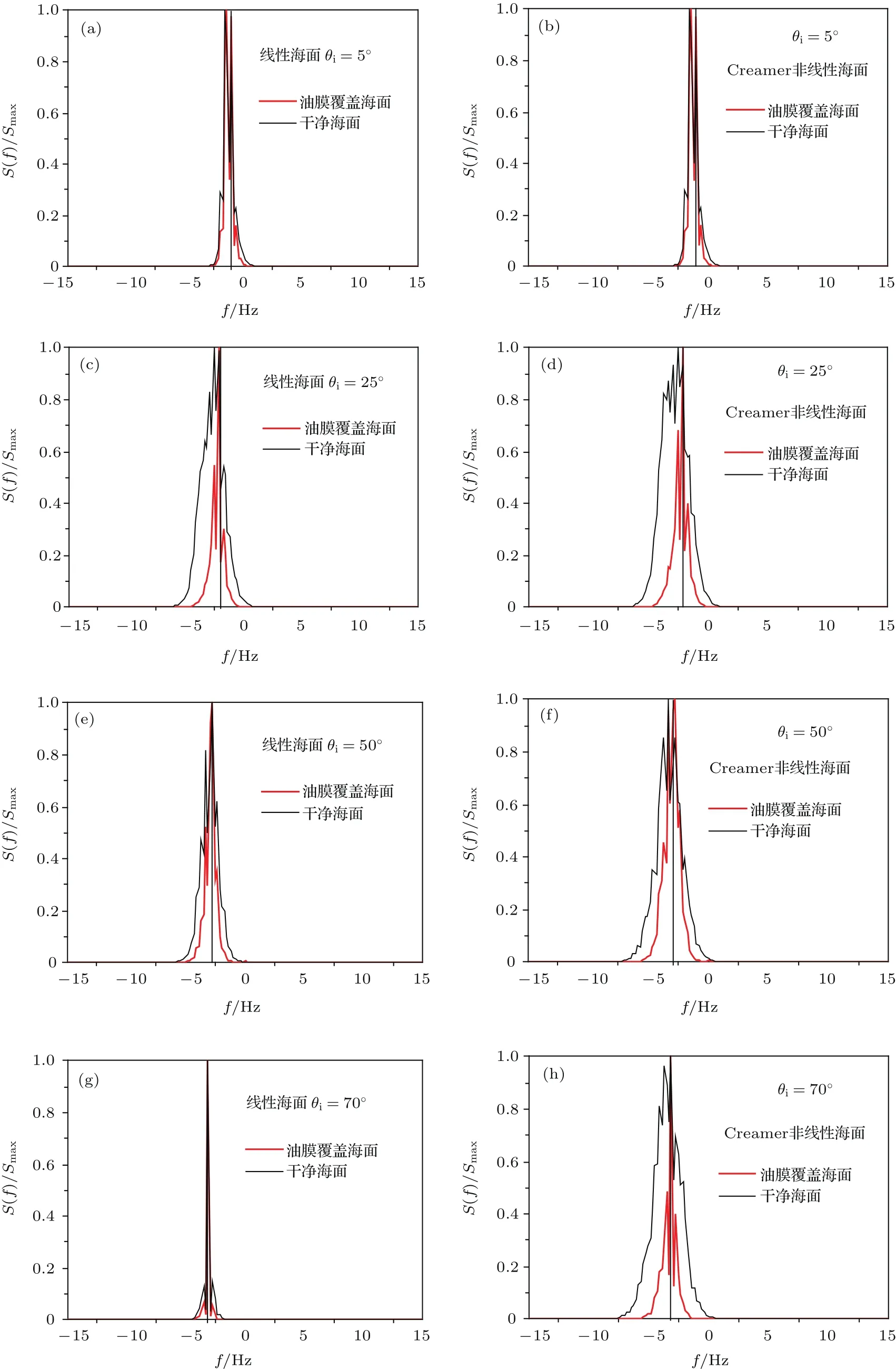
圖7 不同入射角下的線性與Creamer非線性海面散射回波的多普勒譜比較Fig.7.Comparison of the Doppler spectra of scattered echoes from a linear and Creamer nonlinear ocean with different incident angles.

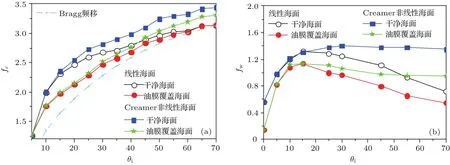
圖8 線性與Creamer非線性海面散射回波多普勒譜頻移與展寬的比較 (a)頻移;(b)展寬Fig.8. Comparison of the Doppler spectra of scattered echoes from a linear and Creamer nonlinear ocean:(a)Doppler shift;(b)Doppler bandwidth.

圖9和圖10給出了不同風速下油膜覆蓋海面散射回波的多普勒譜與干凈海面散射回波的多普勒譜的比較.每幅圖均給出了三條曲線,分別為干凈海面以及兩種不同油膜參數下的多普勒譜曲線,海面模型均采用Creamer非線性模型.海面風速分別為3 m/s和5 m/s.從圖中可以看出,無論風速大小,除了小入射角外,油膜覆蓋海面的多普勒譜與干凈海面的多普勒譜均有明顯差異.首先,相較于干凈海面的多普勒譜,油膜覆蓋海面的多普勒譜明顯要窄一些,即海表面油膜的存在將導致海面散射回波的多普勒譜產生一定的收縮效應.且不同的油膜參數對散射回波的多普勒譜影響程度也不同.在相同條件下,油膜參數為{ξ0=25 mN/m,ωD=11 rad/s}對應的多普勒譜比{ξ0=9 mN/m,ωD=6 rad/s}更窄些.其次,通過觀察不同入射角下的多普勒譜頻移,發現除了小入射角外,海面上方存在油膜時,散射回波的多普勒譜頻移相較于干凈海面變小了.究其原因,無論是多普勒譜的譜寬還是頻移,都與海浪波的軌道速度有關,當海面上方漂浮油膜時,油膜的黏滯阻尼作用將降低海浪波的軌道速度,并且當油膜參數越大,這種阻尼作用更強,才導致多普勒譜的譜寬和頻移與干凈海面有較大差異.

為了定量地比較油膜覆蓋海面和干凈海面的多普勒譜之間的差異,圖11和圖12分別給出了不同風速、不同油膜參數下的多普勒譜的頻移和展寬比較.從圖中可以看出,無論風速大小,油膜覆蓋海面的散射回波對應的多普勒譜頻移與展寬均明顯小于干凈海面的頻移與展寬.原因如上所述,主要是由于油膜阻尼作用降低了海浪波的軌道速度.并且當風速較小時,這種影響作用更大,原因在于風速越小,模擬粗糙海面的PM譜高頻成分越多,油膜的阻尼作用恰好破壞了高頻成分對應的毛細波,故風速越小時,油膜的阻尼作用表現更為明顯,所以無論頻移還是展寬,風速越小時,油膜覆蓋海面回波的多普勒譜譜寬和頻移與干凈海面差別越明顯.

4 結 論

本文基于迭代物理光學方法研究了油膜覆蓋的一維Creamer非線性海面電磁散射回波的多普勒譜特征.通過與線性模型的多普勒譜結果的比較發現,海面的非線性特征對于散射回波的多普勒譜特性影響極大,尤其在大入射角情形下,Creamer非線性海面的頻移和展寬特性同實測數據[26]符合得更好,故本文采用Creamer非線性模型進行油膜覆蓋海面的幾何建模.通過比較干凈海面與油膜覆蓋海面的多普勒譜結果,發現海洋表面油膜的存在將導致海面散射回波的多普勒譜產生一定的收縮效應,多普勒譜頻移相較于干凈海面情形減小,并且多普勒譜的這種差異與油膜參數及風速均有一定的關系.油膜參數值越大時,這種收縮效應越明顯;風速越小時,油膜對多普勒譜頻移影響越明顯.

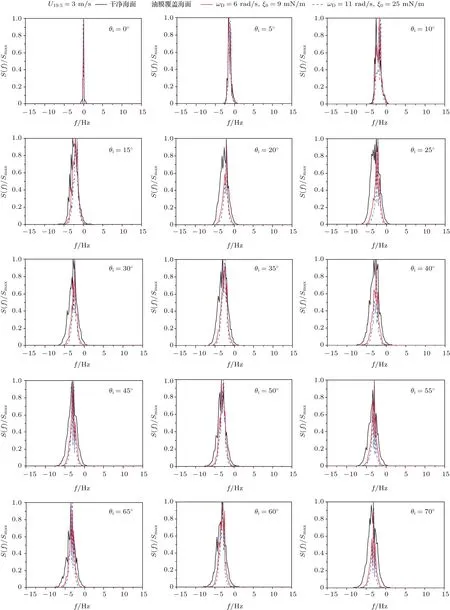
圖9 不同油膜參數下的Creamer非線性海面散射回波的多普勒譜與干凈海面散射回波多普勒譜的比較Fig.9.Comparison of the Doppler spectra of scattered echoes from Creamer nonlinear contaminated ocean with different oil parameters and clean ocean.

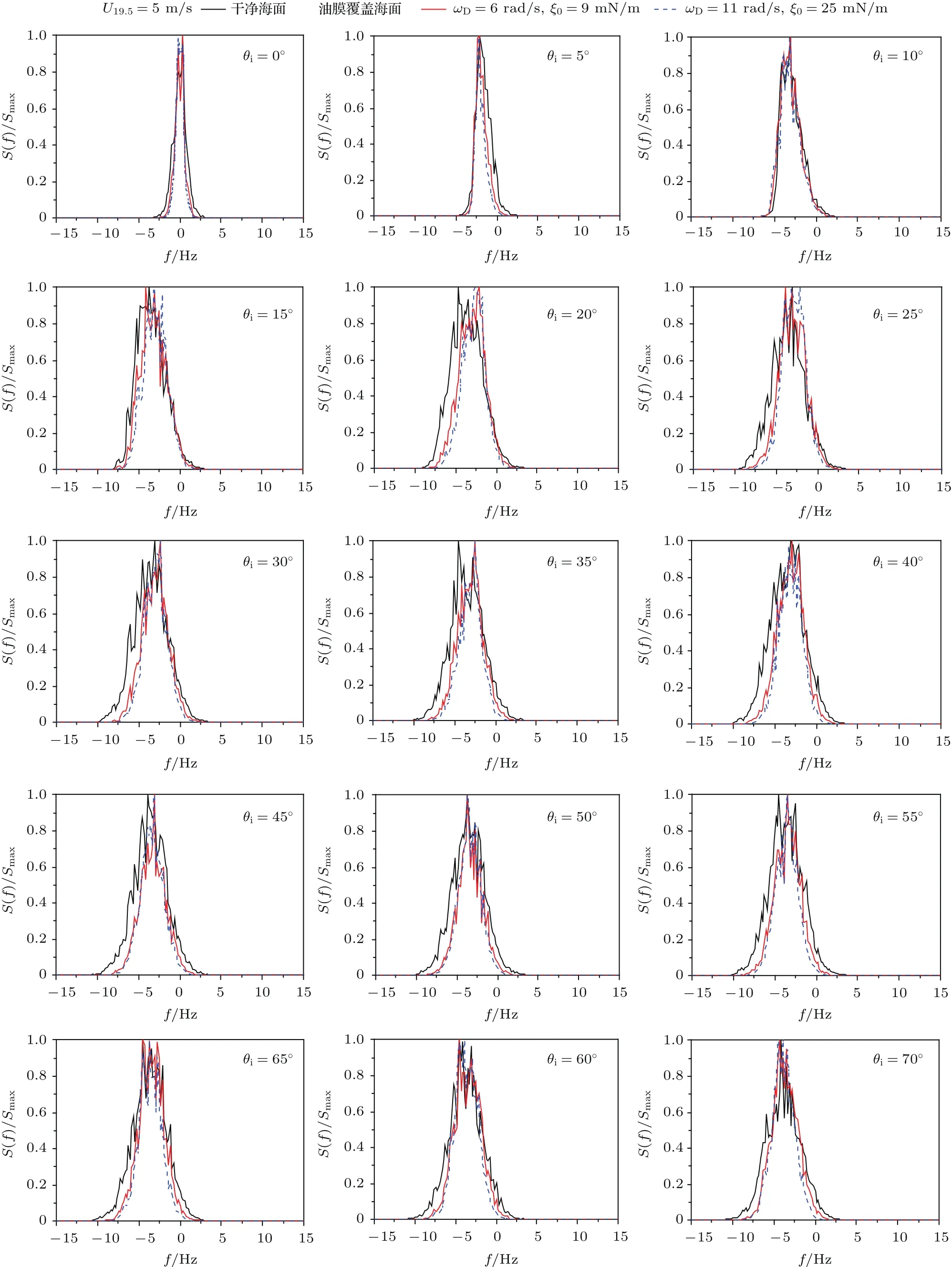
圖10 不同油膜參數下的Creamer非線性海面散射回波的多普勒譜與干凈海面散射回波多普勒譜的比較Fig.10.Comparison of the Doppler spectra of scattered echoes from Creamer nonlinear contaminated ocean with different oil parameters and clean ocean.

圖12 干凈海面與不同油膜參數下海面回波的多普勒譜展寬比較 (a)U19.5=2 m/s;(b)U19.5=3 m/s;(c)U19.5=5 m/sFig.12.Comparison of the Doppler bandwidth of scattered echoes from clean ocean and contaminated ocean with different oil parameters:(a)U19.5=2 m/s;(b)U19.5=3 m/s;(c)U19.5=5 m/s.

本文的不足之處在于所采用的模型為一維海面散射模型,且未研究油膜的厚度與多普勒譜的關系,下一步工作將在二維海面散射模型的基礎上,考慮更為精確的油膜阻尼模型,考察油膜厚度對多普勒譜的影響,并根據結果反演油膜的厚度,為多普勒雷達進行海面油膜檢測提供更有價值的物理理論依據.