齒輪嚙合過程彎曲強度有限元分析*

涂文兵，楊錦雯，羅 丫，任繼文

(華東交通大學 機電與車輛工程學院，江西 南昌 330013)

0 引言

輪齒折斷是機械傳動設備中最常見的齒輪損傷形式，也是造成齒輪失效的主要原因。輪齒受力后，在齒根部產生的彎曲應力最大，且在齒根過渡圓角處有應力集中。齒根的彎曲應力隨嚙合點位置的變化而不同，如果齒根的應力超過了材料的極限應力則會造成輪齒過載折斷。因此，分析齒輪不同嚙合位置時齒根的彎曲應力具有重要的理論價值和工程意義。

齒輪的靜強度研究自齒輪應用以來就受到了國內外學者的重視。Conry[1]通過編程計算得到了齒輪的彈性變形和接觸應力分布；Refaat[2]將變分不等式與有限元接觸分析相結合，計算了齒面接觸應力和齒根應力；陶振榮[3]提出了一種將齒輪接觸疲勞強度的常規設計與可靠性設計相結合的改進計算方法，為齒輪的小型化設計提供參考；徐躍進[4]計算分析了錐齒輪嚙合過程中的接觸應力，并與赫茲公式計算結果比較，證明了有限元仿真法的精確有效性；董淑婧[5]通過兩種加載方案對主、從動齒輪的有限元模型進行分析計算，得到了主、從動輪的彎曲應力；王小群等[6]采用三維接觸有限元技術研究了不同齒根過渡曲線對齒輪齒根彎曲疲勞強度的影響，為選擇不同齒輪加工方法提供了理論依據；郭輝等[7]用三維接觸有限元法計算了面齒輪副嚙合過程中及其參數變化時彎曲應力的變化；陳玲等[8]建立了齒輪二維和三維有限元模型，分別研究了在靜載荷和沖擊載荷作用下齒輪能承受的最大載荷值；趙韓等[9]較系統地介紹了近年來齒輪技術新的發展和應用現狀，并提出了一些需要解決的問題。綜上，目前關于齒輪靜強度的研究主要集中在對齒輪接觸應力的分析方面，較少涉及到齒根彎曲應力，特別是對齒輪不同嚙合位置時齒根的彎曲應力分析。因此，本文對齒輪嚙合過程的彎曲強度進行有限元分析。

1 齒輪嚙合過程彎曲強度有限元分析流程

本文利用有限元分析軟件ANSYS建立一對漸開線直齒圓柱齒輪的接觸有限元模型，并對其進行非線性靜力學分析。通過與理論計算結果的比較，驗證本文所用分析方法的準確可靠性，并在此基礎上進一步分析齒輪不同嚙合位置下齒根的彎曲強度。通過設置不同加載位置來仿真嚙合位置的真實變化，然后求解計算出不同嚙合位置下齒根的彎曲應力，從而得到齒輪彎曲強度隨嚙合位置的變化規律。齒輪嚙合過程彎曲強度有限元分析流程如圖1所示。

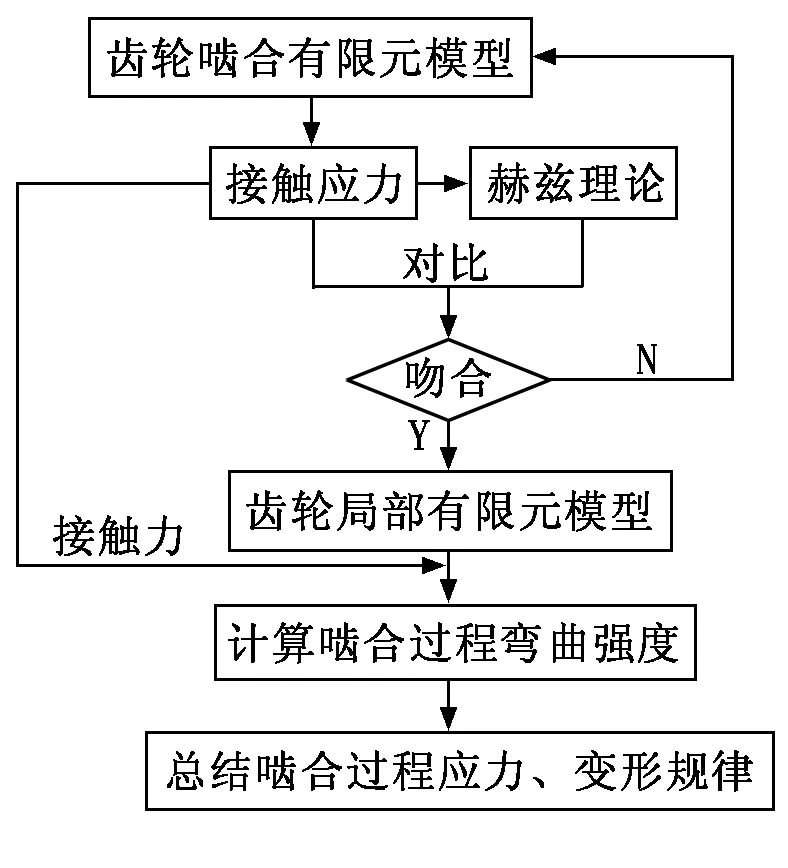
圖1 齒輪嚙合過程彎曲強度有限元分析流程

2 有限元模型建立

本文以漸開線直齒圓柱齒輪為研究對象，其結構參數見表1。

齒輪傳動是依靠輪齒依次嚙合而實現的，正確嚙合的兩漸開線直齒圓柱齒輪的法向齒距Pn必須相等。齒輪的嚙合從主動輪的齒根推動從動輪的齒頂開始，到主動輪的齒頂推動從動輪的齒根結束，輪齒依次嚙合，形成連續傳動，齒輪嚙合過程的齒廓圖如圖2所示。圖2中，N1N2為公法線，B1B2為實際嚙合線，Pn為法向齒距，ra1為主動輪齒頂圓半徑，rb1為主動輪齒根圓半徑，ra2為從動輪齒頂圓半徑，rb2為從動輪齒根圓半徑。重合度計算公式為：

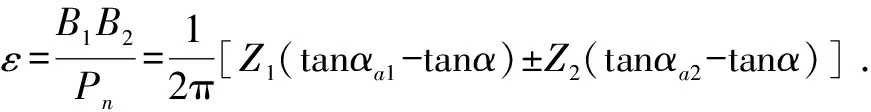
(1)

其中：Z1為主動輪齒數;Z2為從動輪齒數;αa1為主動輪齒頂圓壓力角;αa2為從動輪齒頂圓壓力角;α為嚙合角。已知Z1=24，Z2=48，αa1=29.841°，αa2=25.564°，α=20°。將相關參數代入公式(1)中求得齒輪重合度為1.67，表明齒輪嚙合過程中，單齒對工作與雙齒對工作交替進行，且轉過一個基圓齒距期間有67%的時間是雙齒嚙合，27%的時間是單齒嚙合。由于單齒嚙合時齒輪所受應力最為惡劣，因此本文主要對單齒嚙合過程中齒輪的彎曲強度進行分析。

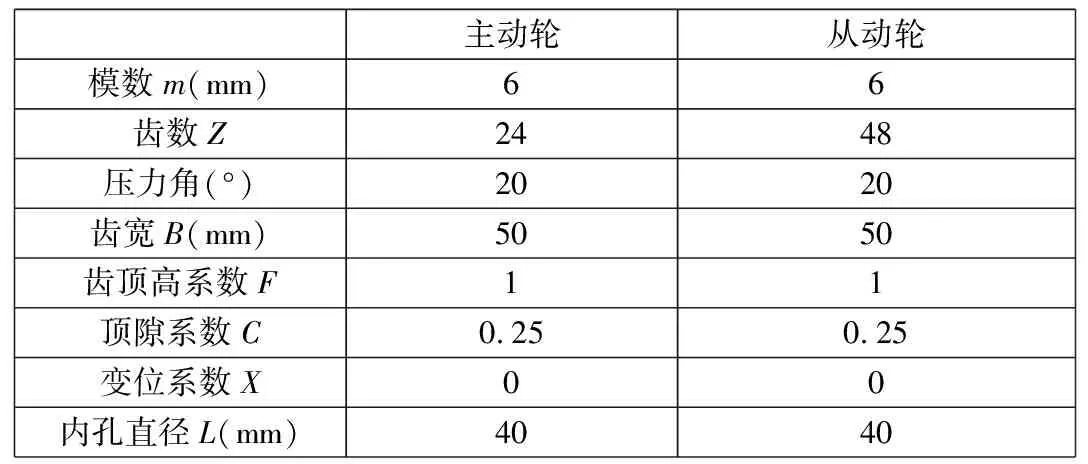
表1 漸開線直齒圓柱齒輪基本參數

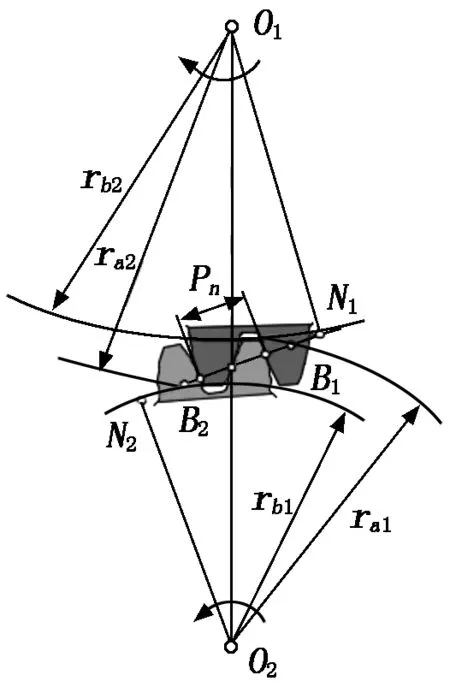
圖2 齒輪嚙合過程的齒廓圖

利用大型建模軟件Pro/E創建齒輪嚙合的實體模型，保存為igs格式后導入ANSYS中。齒輪材料為40Cr，選用各向同性材料進行模擬，設置密度為7 850 kg/m3、彈性模量為2.06×105MPa、泊松比為0.3。選用Solid-brick 8 node 185單元對模型進行網格劃分，為保證計算精度同時節約計算時間，對輪齒嚙合部位進行網格細化，設置全局網格大小為6 mm，齒輪嚙合部位為0.8 mm，最終得到103 632個單元、456 892個節點。齒輪接觸采用點-面、柔性-剛性接觸，設置摩擦因數為0.3。主動輪傳遞的扭矩為487 N·m，齒輪內孔上的節點總數為1 404個，根據齒輪運動規律，對從動輪中心孔上所有節點進行全約束，在主動輪中心孔面節點上施加切向力以模擬扭矩。齒輪嚙合有限元模型如圖3(a)所示。在ANSYS中創建齒輪局部實體模型，設置材料屬性同上。選用Plane183單元對模型進行網格劃分，最終得到5 915個單元、18 234個節點。對齒輪內孔和兩側面進行全約束，得到的齒輪局部有限元模型如圖3(b)所示。

圖3 齒輪有限元模型

3 結果與分析

3.1 齒輪接觸應力分析

用完全牛頓-拉普森迭代算法對齒輪接觸模型進行靜力學求解，得到的齒輪接觸等效應力云圖如圖4所示。從圖4中可以看出：應力主要集中在輪齒接觸處和齒根處，并向四周逐漸衰減，齒輪傳動中齒面受到的最大接觸應力為605 MPa。按齒輪接觸強度的傳統計算方法，接觸應力計算公式為：

(2)

其中：K為載荷系數;T1為主動輪傳遞的扭矩;Φd為齒寬系數;d1為主動輪分度圓直徑;u為傳動比;ZH為區域系數;ZE為彈性影響系數;Zε為重合度系數。已知K=1.81，T1=487 N·m，Φd=0.347，d1=0.144 m，u=2，ZH=2.5，ZE=189.8,Zε=0.881。將已知參數代入公式(2)中，求得接觸應力的理論值為668 MPa，進而算出相對誤差η=9%，由此驗證了本文所用的分析方法的有效性，為下文的嚙合過程齒根彎曲強度分析提供了可靠性保障。

3.2 齒輪嚙合過程彎曲應力分析

在齒輪的運動過程中，輪齒的受力點會隨著嚙合線位置的變化而變化，本文僅對應力最為惡劣的單齒嚙合過程進行分析。在從動輪一側接觸面上設置6個加載位置(如圖5所示)，1為單齒嚙合起始點，6為單齒嚙合終止點。以加載位置的移動來仿真嚙合位置的真實變化，從上文接觸模型的計算結果中提取出接觸力，用靜力等效的原則將載荷均勻地加在接觸表面[10]，求解得到單齒嚙合過程中不同嚙合位置下齒輪的彎曲應力，如圖6所示。

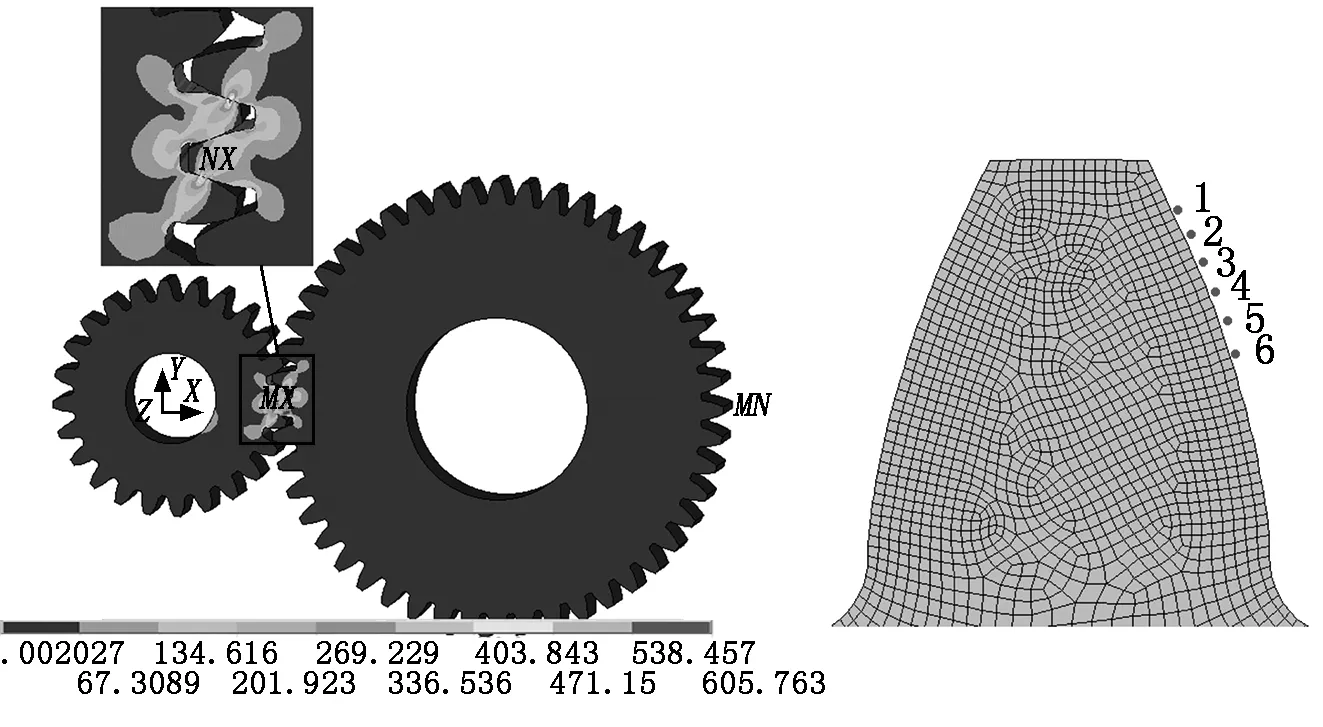
圖4齒輪接觸等效應力云圖圖5加載位置示意圖

由圖6可以看出：在單齒嚙合過程中，受載齒的齒根過渡圓角處出現明顯的應力集中現象，該齒上的應力水平較高，鄰齒和齒輪中心幾乎無應力；當載荷施加在單齒嚙合最高點時，齒根應力最大；隨著嚙合位置的降低，應力分布區域擴展，齒根應力減小；當載荷施加在單齒嚙合最低點時，最大應力位置由齒根處移至加載位置處，齒根應力集中現象得到緩解。

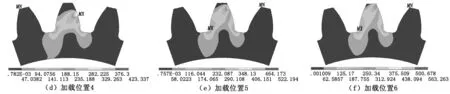
圖6 單齒嚙合過程不同加載位置彎曲應力云圖

為了定量分析齒輪強度與嚙合位置的關系，提取加載側齒根最大應力絕對值、非加載側齒根最大應力絕對值以及齒輪最大變形量進行數據分析，結果如圖7和圖8所示。

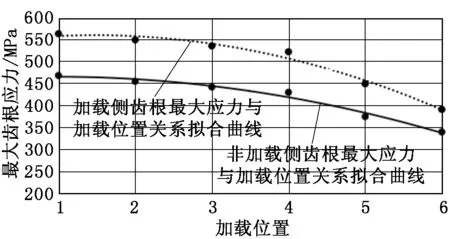
圖7 加載位置與齒根最大應力的關系

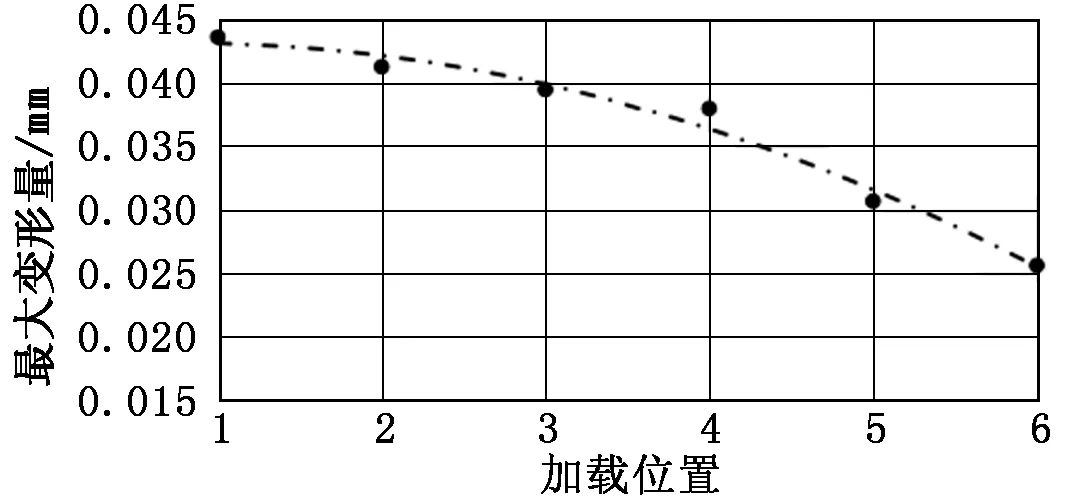
圖8 齒輪最大變形量與加載位置的關系

在單齒嚙合過程中，齒輪加載側受力拉伸，非加載側受力壓縮。由圖7可知：受拉側應力的絕對值始終略大于受壓側應力的絕對值，且材料的抗壓強度遠大于抗拉強度，因此齒輪嚙合過程中最危險的位置為加載側齒根圓角處。通過對數值點進行曲線擬合可知，兩側最大應力在單齒嚙合過程中均呈二次拋物線衰減。

由圖8可知：在單齒嚙合過程中，齒輪的最大變形發生在嚙合的最高點，且位于齒頂圓附近。通過對數值點進行曲線擬合可知，齒輪最大變形量在單齒嚙合過程中呈二次拋物線衰減。

4 結論

本文基于ANSYS對齒輪嚙合過程彎曲強度進行分析，得出如下結論：

(1) 齒輪嚙合過程中最危險的位置為加載側齒根圓角處，持續的應力集中容易造成輪齒的折斷，因此在齒輪的設計過程中應注意提高齒根圓角處的強度。

(2) 齒輪單齒嚙合過程中，兩側齒根彎曲應力和最大變形量均呈二次拋物線衰減。

(3) 鑒于ANSYS分析的快捷、直觀和準確性，在齒輪設計過程中可以使用有限元分析來代替傳統方法進行強度校核，以縮短研發周期，提高設計效率。