數學排隊論模型在通信網中的應用研究

尹皇皓

（大連市第二十四中學，遼寧 大連 116000）

數學排隊論模型在通信網中的應用研究

尹皇皓

（大連市第二十四中學，遼寧 大連 116000）

排隊論是一種數學理論和方法，它是運籌學的一個分支，又稱隨機服務系統理論。排隊是生活中的一種常見現象，滲透人們生活的方方面面。主要論述了排隊論在通信電網中的應用。

排隊論；通信網；平衡模型；電話損失率

排隊論實際上是一種服務系統理論。人們在日常生活中會碰到大大小小的排隊問題，比如排隊選購商品、排隊結賬、排隊等待電梯等。1909年，丹麥數學家A.K.埃爾朗在解決自動電話設計問題時，首先提出了排隊論的理論體系。埃爾朗以熱力學統計平衡理論為基礎，開創性地建立了電話統計平衡模型，并提出了著名的埃爾朗電話損失率公式。埃爾朗的理論研究影響很大，不僅僅解決了電話系統的設計問題，他的理論還被應用于計算機網絡、生產、服務管理、運輸、軍事等多個領域。計算機近幾年的發展十分迅速，它的崛起不僅健全了通信系統，還促進了排隊論的理論研究和應用。

1 通信網與排隊論概述

以往，分隔兩地的人通過信件通信交流，送信過程長且易丟失。隨著通信網的建立，可以讓分隔很遠的兩個用戶迅速實現交流溝通。通信網就是分處異地的用戶之間傳遞信息的系統，但只是點與點之間的溝流交通，不能稱為通信網，這只是通信的基本形式。通信網是由許多的傳輸系統交換后，按照幾何拓撲學組合在一起。排隊論可以用來分析通信網中流量的使用情況。通信網內的流量數據十分龐大，用排隊論分析時并不簡單，但排隊論可以精準地分析特點的節點、路徑上的流量。因此，研究人員通常應用排隊論指導通信網的流量設計。排隊論又稱隨機服務系統理論，就是研究隨機聚散現象、服務系統工作的數學方法。1909年，丹麥數學家A.K.埃爾朗在解決自動電話設計問題時，首先提出了排隊論的理論體系，他提出的著名的埃爾朗電話損失率公式，不僅解決了電話系統的設計問題，對后世也有很深遠的影響，后世數學家基本沿用他的公式研究排隊論。20世紀50年代，堪道爾（D.G.Kendall）系統地研究了排隊論，他受到了概率論中馬爾可夫鏈的研究啟發，進一步完善了排隊論的理論研究，1951年，他提出用A表示顧客到達時間分布，B表示服務時間的分布，C表示服務機構中的服務臺的個數的排隊分類。堪道爾的研究擴大了排隊論的應用范圍，計算機網絡、生產、服務管理、運輸、軍事等多個領域均有涉及，其中，通信領域應用最多。實際需求誕生了排隊論，也會影響排隊論的發展。以下將主要論述排隊論如何提高通信領域的商業價值。

2 排隊論在通信網中的商業運用

排隊是生活中的一種常見現象，滲透了人們生活的方方面面。人們日常中會碰到大大小小的排隊問題，比如排隊選購商品、排隊結賬、排隊等待電梯等。人們的生活需求孕育了排隊論，也必然影響排隊論的發展。在很多領域都可以看到排隊論的應用。本文重點敘述排隊論在通信網中的商業運用。通信網是一個非常龐大的系統，里面也充斥著不少類似排隊的問題，比如電話占線問題，如果電話用戶聯系其他用戶時，中斷線都顯示占用狀態，則該用戶就不能進行正常的通信，必須等待。排隊論是一種分析通信網的數學方法，但通信網內的信息數據過于龐大，綜合分析的難度很大。數據由存儲到轉發的過程也是一個類似排隊的過程。數據并不能直接傳播，到達節點時也需等待處理。像這種需要等待處理的現象都是類似排隊的現象，不同的是，我們的肉眼不能直接觀察到這些問題。這種現象不止存在于通信領域，科學研究的很多領域都存在排隊現象。如圖1為多隊多服務臺系統。

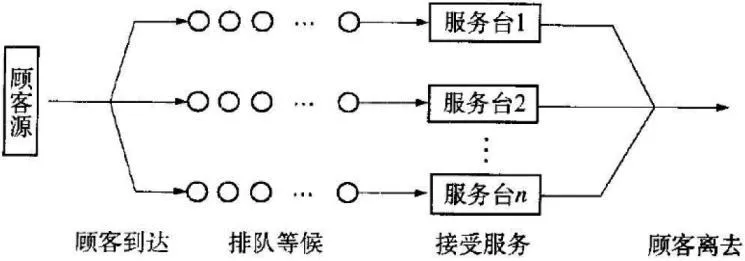
圖1 多隊多服務臺系統

排隊論實際上是一種服務系統理論，因此，都存在被服務者和提高服務者。我們可以把通信網中要求服務的人稱為客戶，接受服務要求并提供服務的一方稱為服務機構（機器設備、信息網等），中繼線、信道等類似接收、傳達服務信息的設備可以形象地比喻為服務窗口。通信網運行時，客戶提供要求的時間、數目都是不確定的，因此，提供服務的時間也是不確定的。客戶數目、要求未知，但是提供服務的設備有限，當客戶要求超出服務設備所能承受的范圍時，客戶就必須等待，這就是排隊現象產生的原因。服務設備的數量與客戶需求之間的關系在一定程度上可以決定服務的質量。如果客戶要求超出服務設備所能承受的范圍，客戶就需要排隊等候，排隊時間越長，不滿意的程度越高；如果客戶要求未超出服務設備所能承受的范圍，排隊現象就會減少，客戶會比較容易得到滿足感。排隊的規則可以分為三類，按照服務設備的數量和客戶使用服務設備的時間長短等劃分為：①等待制。所有服務窗口、服務員都不能提供服務，客戶只能按到達的先后順序排隊等待，有時會有插隊現象。②損失制。客戶排隊等待時，失去耐心、有其他事情待進行等離去現象。③混合制。混合制即以上兩種現象都存在。

3 結束語

通信網是一個非常龐大的系統，排隊論是一種分析通信

網很好的數學方法，但是通信網內的信息數據過于龐大，即使是排隊論總體分析也很困難。排隊論誕生于1909年，由丹麥數學家A.K.埃爾朗提出，之后由堪道爾（D.G.Kendall）

進一步完善。人們的生活需求孕育了排隊論，也必然影響排隊論的發展。排隊論主要應用于通信系統，通信系統涉及的因素太多，用一般的數學模型很難統籌兼顧，分拆成小的節點研究有利于問題的解決，因此，排隊論是一種重要的研究通信網的數學方法。

［1］何勇.互聯網通信中的信息選取與分布問題的建模與求解［J］.計算機學報，2001，24（06）.

［2］房文治.網絡建設安全性分析［J］.電子世界，2015（15）.

［3］林妍君.計算機通信網絡安全維護措施分析［J］.網絡安全技術與應用，2015（10）.

［4］王志凌.淺談數據加密技術在計算機網絡通信安全中的應用模式［J］.通訊世界，2015（16）.

TP399

A

10.15913/j.cnki.kjycx.2018.01.153

2095－6835（2018）01－0153－02

〔編輯：張思楠〕