數學核心素養視角下“情境-問題”

陳冠峰

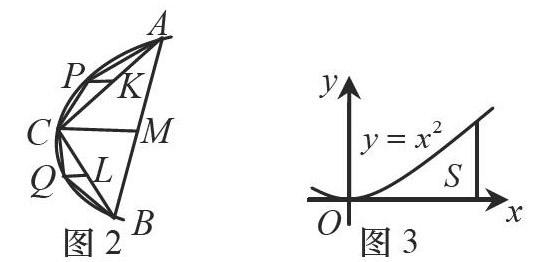
1 問題提出

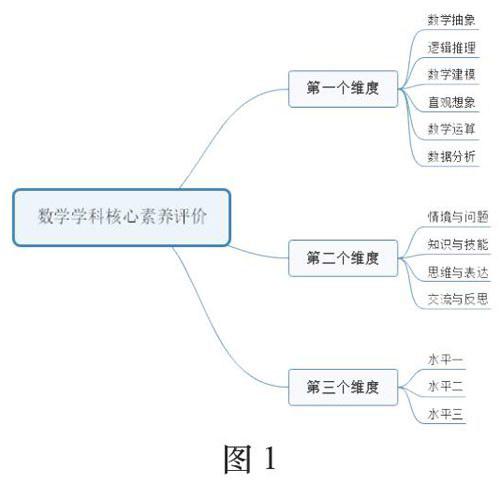
新修訂的《普通高中數學課程標準（2017年版）》指出：“數學學科核心素養包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析六個部分內容”，要求學生通過高中階段學習，掌握“四基”，發展“四能”，如何培養學生學科核心素養，當前的教育界主要聚焦兩個方面問題：一是如何將數學核心素養的培養落實到日常教學，二是如何對學生的數學核心素養進行評價.針對第二個問題，《課標》提出，要構建基于數學學科核心素養的評價框架，包括三個維度的內容，如圖1所示：

在第二個維度中，提出了“情境一問題”的教學.所謂“情境一問題”數學教學，指的是教師創設一定的數學情境，提出問題，學生在教師的引導下，通過發現、提出、分析、解決問題，提煉數學思想方法，構建數學知識體系，形成數學思維品質.數學問題是學生學習數學的驅動力之一，也是課堂評價的重要形式，通過課堂評價，能幫助教師在了解學生對知識掌握情況的基礎上，及時調整自己的教學手段和方法，從而實現教與學的共同提高，對落實學科核心素養評價研究具有重大現實意義.本文以高中數學人教A版選修2-2《定積分概念》-節為例，談談如何構建恰當的數學情境，提出合適的數學問題，從而有效地發揮課堂評價作用.

2 課堂案例

2.1 引入

問題情境1我們已經知道三角形面積的求解方法，同樣，長方形（正方形）、平行四邊形以及多邊形的性質，使我們對于這些圖形的面積都賦予了確定的含義.另外，我們也知道了一種由曲線圍成的圖形——圓的面積計算方法，但是，到目前為止，我們對由曲線所圍成的其他圖形面積求解方法，還知之甚少，比如弓形.同學們考慮考慮，有什么合適的方法用來求解弓形的面積？

點評“問題情境l”的創設，是從最基本的平面圖形之一——三角形展開的，隨后立刻把本節課的研究目標鎖定在“面積”上，而且是帶有“曲線”圖形的面積.開門見山的同時，也讓學生了解，不管多么復雜的數學問題，都是從最基本的概念出發的，這也是邏輯推理的基本形式.

問題情境2 早在古希臘時期，數學家就開始研究這一方面問題.公元前三世紀，全能科學家阿基米德利用窮竭法推算出了弓形的面積，如圖2，請同學們體會一下他的工作是如何開展的？

點評從AC，BC的中點K，L作平行于弓形所在圓直徑（線段MC所在直線）的直線，交弓形于P，Q兩點，則弓形與MBC之間的部分，可以由AAPC和ABQC的面積“近似代替”.

同理，取線段AP， CP， CQ，BQ的中點，分別作平行于MC的直線，分別交弓形于四個點，又可得到四個小三角形，空白部分的面積就可以再由四個小三角形的面積“近似代替”.如此繼續，阿基米德實現了對弓形的“分割”，用這些三角形的面積之和“逼近”弓形的面積，并“近似代替”，此乃“窮竭法”思想.

通過富有濃厚數學味道的數學文化情境構建，適當借助信息技術手段，激發學生學習興趣，還可以在課后交流探究“窮竭法”在其他圖形中的應用，讓學生在具體情境中感悟數學本質.

2.2 探究發現

教師給出“曲邊梯形”的概念后，并以拋物線y= x²，直線x=l以及x軸所圍成的平面圖形為例（如圖3）.

問題情境3 借鑒阿基米德“窮竭法”思想，我們如何通過“近似代替”，求這個曲面梯形的面積？

探究1：如何分割？用怎樣的“直邊圖形”近似代替？有幾種方案？

探究2：哪種方案更合理？如何求分割后直邊圖形的面積之和？

點評 這是本節課的重點，可以采取學生分組交流討論的形式，小組匯報近似代替的方案（矩形過剩估計、矩形不足估計、梯形估計），教師要引導學生比較三種方案的優劣，選擇便于計算的兩種方案：過剩估計和不足估計，并再次分組，讓學生嘗試求出面積之和.

在小組交流展示過程中，教師要根據學生提出的方案，評價學生知識掌握情況，對于不恰當的思路，要進行及時地校正，并注意引導學生嚴謹地運用數學語言，交流和表達自己的觀點.

問題情境4如何表示分割越來越細，直邊圖形越來越多時它們的面積之和？隨著分割越來越細，采用過剩求和與不足求和所得到的結果呈現怎樣的變化和聯系？

點評 這是本節課的難點，即極限的思想，教師要引導學生發現這一事實：不足估計值和過剩估計值隨著n的增大，越來越接近同一個常數，隨后，教師應該指出，正是因為這兩種逼近方式得到同樣的常數，才初步證明了曲邊梯形面積的存在，當然，這種理論上的證明，高中階段不做要求，是高等數學研究的內容.

由于“極限”是高中階段難點概念之一，各小組對于“問題情境4”得出的結論，直接反映出組內學生對于“極限”思想的認知程度，因此，教師要積極主動地對小組結果進行評價，適時對求曲邊梯形面積的四個步驟：“分割——近似代替——求和——取極限”進行總結，培養學生數學抽象、數學運算、邏輯推理素養，提高教學有效性，當然，“極限”這個概念，對于高中生而言，確實較難理解，課堂上教師也可以結合信息技術手段，演示“近似代替”的過程，以此來輔助教學.

3 教學反思

在利用“情境一問題”課堂教學評價時，需要注意以下幾個問題：

3.1“情境-問題”的創設，需要文化融合

數學是有歷史積淀的，數學也是在不斷發展的，本節課以阿基米德的“窮竭法”這一數學文化背景作為引入，一方面是讓學生通過類比，更好地體會曲邊梯形面積的求解策略;另一方面，更重要的是讓學生了解數學中極限思想的起源和背景，激發學習興趣的同時，體會數學科學價值、文化價值和應用價值，形成正確的數學觀.

3.2“情境-問題”的解決，需要師生協作

數學核心素養下，學生的課堂主體地位更加突出，圍繞著“情境一問題”的探討，學生是解決問題的主角，教師是組織者和協作者;同時，課堂上要注重學生知識的形成過程，在學生探求問題的同時，構建知識體系，提升核心素養;另外，在問題解決過程中，也應該重視信息技術的運用，幫助學生更好地理解數學、掌握數學.

3.3 “情境一問題”的評價，需要講究策略

課堂教學評價具有導向、激勵、診斷、改進、反饋等功能，“情境一問題”的評價，應當更注重診斷和改進的功能，同時，應該把握以學生為中心的原則和發展性的原則，采取不同的評價方法，如紙質評價、口頭評價、課堂觀察、信息數據收集等方法，教師要兼顧學生整體學習情況和個體學習進展，在關注學生對知識技能掌握的同時，更多地關注學生數學核小素養的發展.

總之，本節課以“曲邊梯形面積的求解”為主線，圍繞四個情境問題的提出展開教學，學生通過情境問題的探知，構建知識體系，教師通過情境問題的解決方案，適時評價課堂教學，及時調整教學策略，從而有針對性地開展教學活動，在充分提高課堂教學有效性的同時，提升了學生的數學核心素養.

參考文獻

[1]曹一鳴，李俊揚，秦華.我國數學課堂教學評價研究綜述[J].數學通報，2011 （50）：1

[2]楊溆萍，重新審視課堂教學評價的功能、內容與標準[J].教育理論與實踐，2009 （29）： 44

[3]段志貴.基于新課程標準的數學課堂教學評價[J].教育探索，2008 （10）：208

[4]史寧中.高中數學核心素養的培養、評價與教學實施[J].中小學教材教學，2017 （5）：4

[5]教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018：1一180