橢圓與雙曲線比一比
張圣官
讓我們先來嘗試以下兩道題:
題1某圓錐曲線上一點P到兩個焦點F1,F2的距離滿足PF1∶F1F2∶PF2=2∶3∶4,求該圓錐曲線離心率的值.
題2(1)設橢圓的左、右頂點分別為A1,A2,線段CD是垂直于橢圓長軸的弦,連結A1C,A2D并延長相交于點P,則動點P的軌跡方程是________;
初學圓錐曲線時,有畏難情緒很正常.全新的知識,而且是重難點比較集中的地方,那么該怎樣攻克這個“攔路虎”呢?在比較中學習,不失為一種高效的方法.
在題1中圓錐曲線可能有兩種形態:橢圓或雙曲線,離心率的值為.在題2中運用交軌法求軌跡,結果發現在橢圓1中動點P的軌跡方程就是雙曲線;而在雙曲線中動點P的軌跡方程恰好是橢圓.
其實,橢圓與雙曲線有許多相關、相似又相異的性質,需要我們在學習的過程中運用比較法進行探討,在辨析中加深對相關知識的掌握.
一、比較中認識橢圓與雙曲線
初學時,標準方程和圖象是我們主要的抓手.
標準方程中,需要對a,b,c三個量清楚明了,焦點所屬的軸不同,其最終方程也會不同;圖象則是包羅萬象,既要能很快根據已知條件畫出草圖,又要能根據圖象得出基本量.
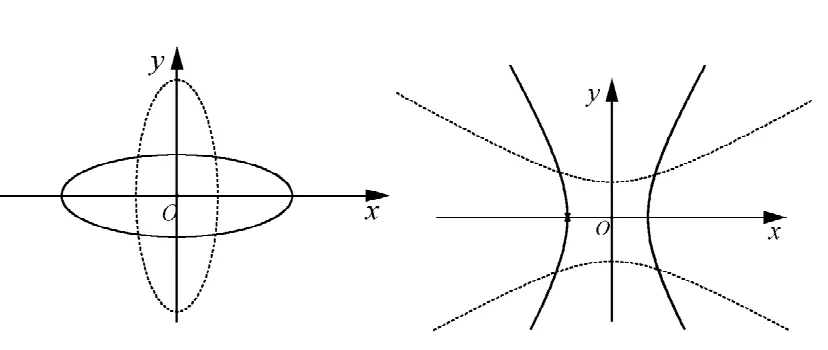
圖1
細心觀察、琢磨教材中的定義,我們可以發現,橢圓和雙曲線的定義與標準方程的差別僅在“和”與“差”上,抓住矛盾的兩個方面,可以將橢圓的性質類比到雙曲線上.隨之而來的圖象,可以看到橢圓的準線像彈簧的兩端,拉著橢圓往外“跑”,而雙曲線的準線則在中間,仿佛阻撓著其兩支往中間擠,還有著標志性的漸近線.
二、比較中探究橢圓與雙曲線性質
探究一:橢圓兩焦點為F1,F2,點Q為橢圓上除頂點外的任一點,過點F2作∠F1QF2的一個外角平分線.的垂線,垂足為P,則點P的軌跡是圓的一部分.
(1)證明此命題為真命題.
(2)你能否類比到雙曲線上,給出一個類似的命題?并證明.
分析仔細體會動點的運動過程,出現外角平分線,才有垂足,于是可自然猜想到將“外角平分線”類比為“內角平分線”;在具體論證的過程中我們可以邊探究邊印證,進而歸納總結,得出結論.類比不是簡單的生搬硬套,必須遵循兩者定義的區別.
探究二:已知橢圓b>0)上A,B兩點關于原點對稱,點P是橢圓C上任意一點,且點P與A,B兩點均不重合,設直線PA,PB的斜率分別為k1,k2,那么k1·k2是否為定值?
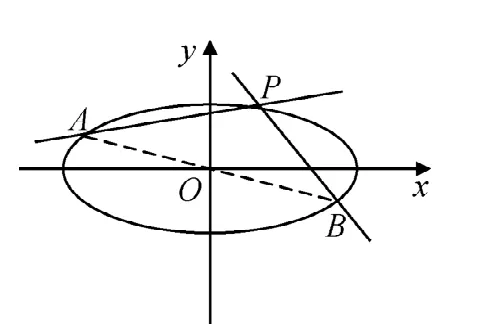
圖2
(1)猜想結論,并證明.
(2)類比到雙曲線中,寫出一個類似的命題,并證明之.
分析探究過程可以從特殊位置開始,猜出結論,再進行一般論證.類比到雙曲線時,引導根據兩個曲線的定義差別,找出類比的規律.
探究三:如圖,點P(x,y)(x>0,y>0)是雙曲線上的動點,F1,F2是雙曲線的焦點,點M是∠F1PF2的平分線上一點,且.某同學用以下方法研究:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得.類似地:點P(x,y)(x>0,y>0)是橢圓上的動點,F1,F2是橢圓的焦點,M是∠F1PF2的平分線上一點,且,則的取值范圍是_________.

圖3
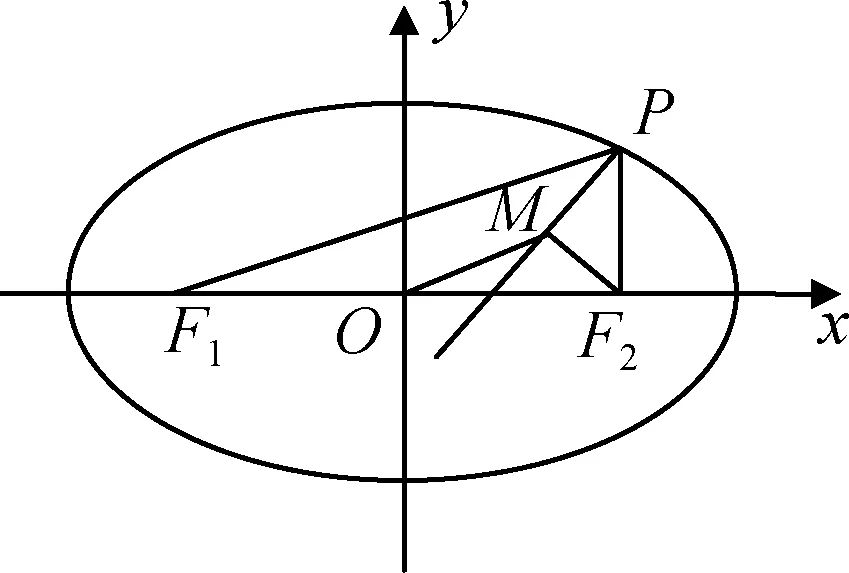
圖4
前面都是橢圓類比到雙曲線,此題是由雙曲線類比到橢圓,而且與探究一有相似之處,可以加強我們對橢圓、雙曲線定義的理解,另一方面也是類比思想的深化.
三、比較中區別橢圓與雙曲線不同點
橢圓與雙曲線同屬于圓錐曲線,但形狀不同,不是所有性質都一樣.在橢圓中,有四個頂點,兩條準線,圖形是封閉的;在雙曲線中,有兩個頂點,兩條準線,圖形是開放的,而且有兩條漸近線.有關漸近線的問題是雙曲線所特有的,而橢圓就沒有.有些結論相似但不相同.例如:過橢圓0)的左焦點F作直線與橢圓交于A,B兩點,則以線段AB為直徑的圓與橢圓的左準線相離;過雙曲線的左焦點F作直線與雙曲線的左支交于A,B兩點,則以線段AB為直徑的圓與雙曲線的左準線相交.這是由于它們離心率范圍不同造成的.類比也不能太“任性”.
例1△ABC中,B,C分別是雙曲線的左、右焦點,A在該雙曲線的右支上運動.△ABC的內切圓圓心為I,求證:I的橫坐標為定值.
證明設內切圓分別與AB,BC,CA切于D,E,F,則AD=AF,BD=BE,CE=CF.因為A在該雙曲線的右支上,所以4=AB-AC=BD-CF=BE-CE.設E(x0,0),則,所以x0=2.因此I的橫坐標為定值2.
例2如圖,設橢圓的右焦點為F,直線l與曲線C:x2+y2=16(x>0)相切,且交橢圓E于A,B兩點,求證:△FAB的周長為定值.
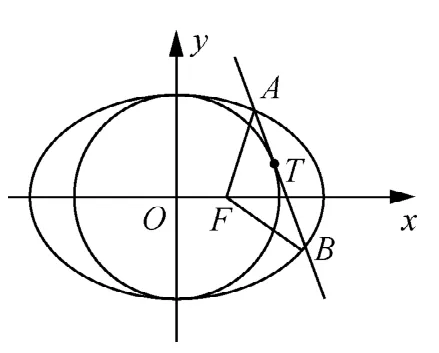
圖5
解設切點為T,連結OT,OA,設A(x1,y1),x1>0.
在圓x2+y2=16中,,將代入得.
同理可得BT+BF=5.即△FAB的周長為定值10.

