初中數學教學中的類比法運用
劉 勇
(江蘇省南通市實驗中學 226001)
一、運用類比進行知識聯系的構建
1.類比生活實際
將學生熟悉的生活背景與數學知識融合在一起并通過類比教學能使學生更好地掌握數學的本質與模型.
例如,教師在“合并同類項”這一內容的教學中可以創設以下情境:
(1)實物歸類:教師首先將形狀為圓、方形、三角形等學習用品混在一起,請學生根據自己的標準將這些學習用品進行分類并要求學生回答如下問題:①你是根據什么標準進行分類的?②分類標準一樣的情況下分類方法唯一嗎?③你心中的分類方法有哪些?
(2)觀察多項式-2x+8y-4z+x-y并回答以下問題:①哪幾項可以歸為一類呢?②你分類時的依據是什么?那么3a2b-4ab2-3+5a2b+2ab2+2ab-6ab+8應怎樣歸類呢?
學生在實物分類到數學分類的活動中往往會感到數學的可親可近,數學的神秘和抽象對于學生來說也隨之消除很多,學生在熟悉的生活背景下對類比法也形成了更加真切的感受與理解,數學和實際的聯系也因此得到具體的體現.
2.類比舊知
運用類比法進行新概念的引入往往能令學生對新概念的內涵與外延形成更好的理解,數學概念的類似也在類比法的運用中而變得更易理解與掌握.
例如,教師在教學“分式”這一內容時可以首先利用類比分數的方式導出分式的概念、分式的基本性質與運算法則.具體操作如下:第一步,引導學生回顧小學階段學過的分數的概念;第二步,回顧分數的構成以及分母不能為零的特點;第三步,回顧分數的分類并將分數的概念延伸到代數式中,繼而獲得分式的概念;第四步,在學生掌握分式概念的基礎上明確分數和分式之間的區別.
二、在類比中鍛煉學生思維
1.類比操作
例如,教師在“角的比較與運算”這一內容的教學中可以這樣落實類比操作:首先引導學生對線段的比較方法進行復習與回顧,然后引導學生嘗試對兩個角的大小進行比較,學生在教師的這種類比操作中自然會聯想到線段比較中的度量法與疊合法,最后,教師再引導學生對角的比較法與注意事項進行歸納時,學生在一定的經驗與知識基礎之上進行總結與歸納也就水到渠成了.
2.類比計算
例如,學生在六十進制的角的度數換算中往往會覺得頗有困難,因此,教師可以引導學生在以下的設計中充分運用類比計算進行學習:
第一步:計算:0.8米=____分米,0.8小時=____分鐘,引導學生對這兩個計算進行觀察并發現其共同點,使學生建立高級單位向低級單位換算需要乘以進率的概念.
第二步:計算:0.8°=____′,5′=____″.學生在這樣的計算經歷中自然會聯想到類比法,反向亦是如此.先請學生計算30分米=____米,30分鐘=____小時.
第三步:引導學生對低級單位向高級單位轉換的規律進行自主歸納并進行一定的換算運用.
3.類比探究
例如,“線段”這一內容中的一道題:若一線段上有n個點,則共有多少條線段呢?
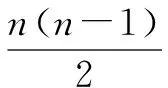
“一元二次方程”中的一個問題也可運用類比思想進行解決:出席某次聚會的每位代表都會與其他各代表均握手一次,統計結果為共握手45次,則參加聚會的代表共有多少呢?
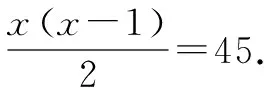
上述兩個問題雖然有一定不同,但其本質卻是相同的,學生在解決第一個問題的基礎上再求解第二個問題也會容易很多.
4.類比歸納
對兩種或兩種以上在某些關系上具備一定相似特征的對象進行對比與歸納的研究方法即為類比歸納,學生在知識的類比與歸納中往往能將知識體系構建得更加有序和系統.
例如,教師在“一元一次不等式的解法”這一內容的教學中可以首先對一元一次方程的解法進行復習,然后引導學生對一元一次不等式的解法進行討論,使學生在類比討論中獲得其解法與步驟.
5.類比猜想
運用類比對兩個對象或問題的相似性進行比較并獲得數學新命題或方法的猜想即為我們經常運用的類比猜想,對命題本身或解題思路方法進行類比繼而產生猜測都是獲得命題推廣與引申的原動力.
例如,教師在“等腰梯形同一底邊上的兩底角相等”這一內容的講授中,首先可以引導學生對“等腰三角形的性質”進行回顧,然后引導學生在此基礎上上進行類比猜測并加以驗證.
由此可見,發現解題思路、導入新概念、記憶與證明公式定理、探索研究新知識等數學學習的多個方面都需要運用到類比法,類比法在數學教學中的運用對學生的知識建構、能力發展都能起到很好的作用.因此,教師應充分認識到類比法的價值,根據不同的教學對象落實不同的類比方法以促進學生知識與能力的發展.

