“亞黃金橢圓”的新定義及性質

劉娟娟 羅文軍

(1.甘肅省秦安縣郭嘉鎮槐川初級中學 741609;2.甘肅省秦安縣第二中學 741600)

筆者在文[1]中給出了亞黃金橢圓的5個性質，為本文的性質1到性質5.在文[2]中給出了亞黃金雙曲線的定義和6個性質，在文[3]中又給出了亞黃金雙曲線的8個性質.

筆者在教學之余又得出了亞黃金橢圓的新定義及3個性質，3個性質為本文中的性質6到8現.介紹如下以供參考.

為了本文探討亞黃金橢圓性質的需要，這里須對一些概念作些說明.

黃金矩形的定義：

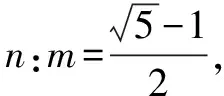
為了以下性質探究的方便，在不影響亞黃金橢圓性質的條件下，做兩點假設：

第一，以橢圓的中心為原點，兩焦點所在直線為x軸建立直角坐標系；

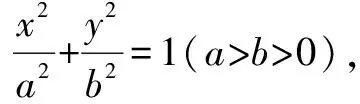
一、亞黃金橢圓的新定義

二、亞黃金橢圓性質的探究

性質1 在亞黃金橢圓中，兩條互為共軛直徑所在直線的斜率(斜率存在)之積為-e4.

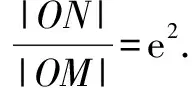
性質3 不平行于亞黃金橢圓對稱軸的切線斜率與經過該切點和中心的直線斜率之積為-e4.

性質4 不平行于亞黃金橢圓對稱軸且不經過橢圓中心的弦所在直線的斜率與經過該弦中點和橢圓中心的直線斜率之積為-e4.

性質5MN是經過亞黃金橢圓中心的弦，T是亞黃金橢圓上任意一點(頂點除外)，如果TM,TN的斜率都存在且不為0，則kTM.kTN=-e4.

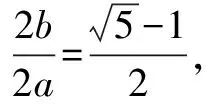
所以由直線x=a,x=-a,y=b,y=-b所圍成的矩形為黃金矩形.

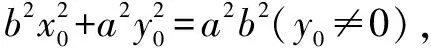
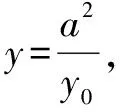
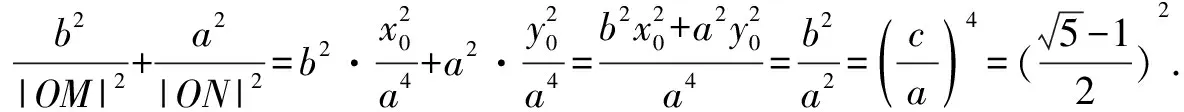
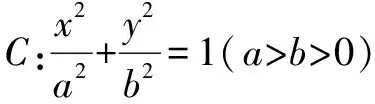
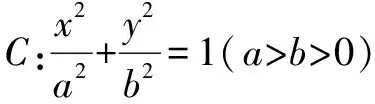
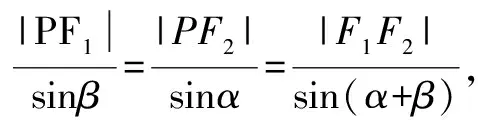
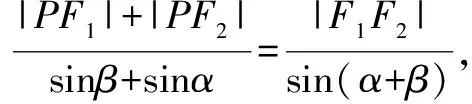
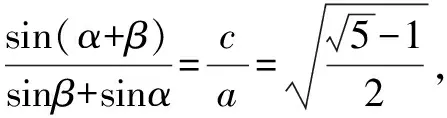
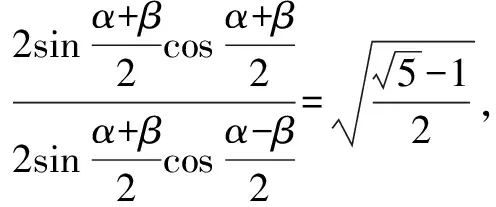
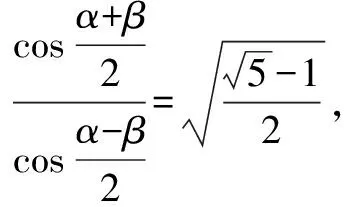
由合分比定理得