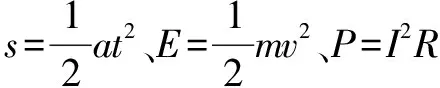巧用函數與方程思想解決物理問題

董倩玉

(河北省內丘中學 054200)

函數與方程思想是一種重要的數學思想，主要是指將一些非函數方程的問題通過構造和轉化，變成有關函數方程的問題，從而運用函數與方程的有關性質和規律來進行問題的解決.高中物理知識反映的是物體運動、變化、功能轉化等過程中所遵循的基本規律，這就與數學的函數方程研究的量與量之間的關系具有一致性.因此，在高中物理問題的分析和解決中進行函數與方程思想的運用，更有利于揭示物理的變化規律本質，有效的解決問題.

一、解決動態變化問題

在高中物理力學和運動學的問題中，常常有些動態變化的量，這就要求我們能夠根據物理知識將其中的關系式列出，將物理的動態變化問題轉化為函數與方程問題，這樣在根據函數與方程的性質進行問題的分析，往往更有效.

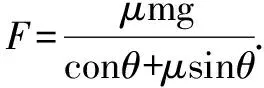
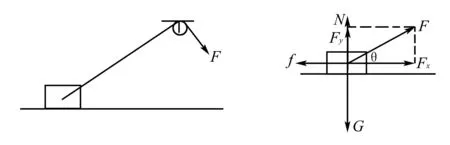
圖1 圖2

根據求出來的拉力并不能判斷F力的變化，因此，我們可以將問題轉化為F與θ之間的函數關系，這樣根據函數的性質就可以對F力的大小變化進行判斷，問題也就迎刃而解了.

二、解決相遇問題

在高中力學中，常常有一些相遇問題，如果我們用函數與方程思想對問題進行分析和解決，將運動相遇學問題轉化為函數與方程問題，就會簡單的多.

圖3

比如圖3中有一個以角速度ω旋轉的圓筒，圖示為其橫截面，一顆子彈沿著圓筒的直徑d穿過圓筒，圓筒對子彈的阻力忽略不計，a、b兩點是子彈穿過圓筒留下的彈孔，∠aOb=θ，求子彈的速度v？

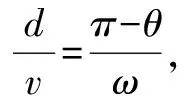
三、解決電學問題

運用函數與方程思想進行電學問題的思考和解決，同樣會起到良好的效果，不僅能增強我們跨學科解決能力，同時也能提升我們的物理解題能力，將所學的知識融匯貫通.比如我們要設計一個電熱爐，要求輸出功率為2.1kw，已知電線電阻為1Ω，采用220V電壓供電，那么求電熱絲的阻值R是多少？

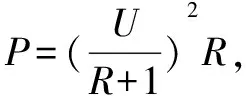
四、解決輸電問題

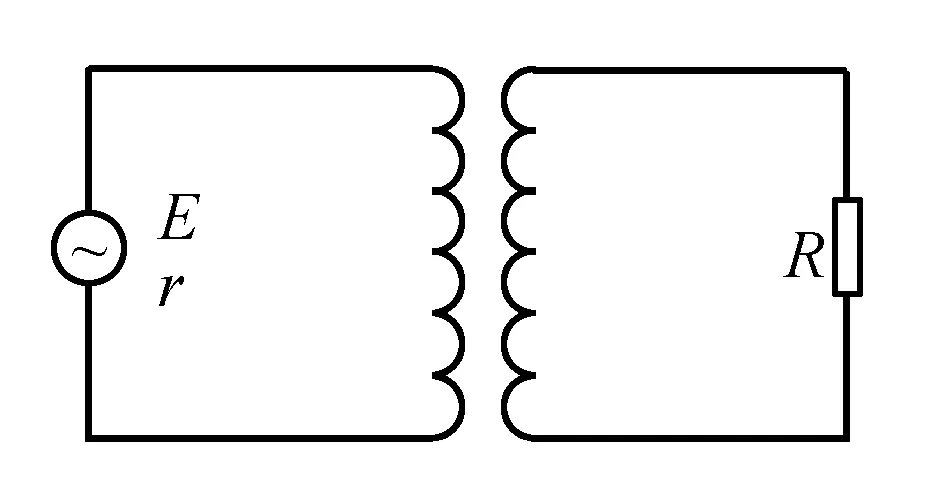
圖4

在解決理想變壓器問題的時候，運用函數與方程思想可以根據物理規律和條件列出相關方程，然后進行求解，得出答案.比如圖4所示的理想變壓器，原線圈和電源相連，已知電源電動勢為E，內阻為r，輸出交變電流，副線圈連接阻值為R的電阻.那么，原、副線圈的匝數比為多少時，電阻R的功率最大，值是多少？