算兩直線交點坐標解圓錐曲線解答題

李 寧

(海南省海南中學 571158)

在圓錐曲線解答題中，有時候需要算出兩直線的交點坐標來參與下一步的求解. 而此時的直線往往是動直線，直線方程含有參數，算出來的交點坐標往往結構比較復雜. 為了能夠順利算出交點坐標，可向學生介紹解線性方程組的克萊姆法則.

(1)求橢圓C的方程；

(2)已知A為橢圓的左頂點，過橢圓C內一點M(1,0)作斜率為k1的直線l與橢圓C交于P,Q兩點，若點N為△APQ的外心，直線ON的斜率為k2，求證：k1·k2為定值.

(2)設P(x1,y1),Q(x2,y2)，直線l：x=my+1，代入x2+4y2=4，

整理得：(m2+4)y2+2my-3=0，

又A(-2,0)，則AP的中垂線方程為(x+2)2+y2=(x-x1)2+(y-y1)2，

(1)求橢圓的方程；

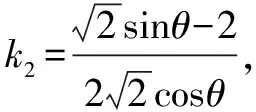
(1)求a,b的值；

(2)求證：直線MN的斜率為定值.

①假設AC,BD，AD,BC四條直線的斜率均存在.

②若AC,BD，AD,BC四條直線中有直線斜率不存在，由題意此時只能有一條直線斜率不存在.

不妨設直線BD斜率不存在，此時D(-2,1)，直線AC：y-1=k1(x-2).

令x=-2，解得此時M點坐標(-2,1-4k1).

綜上所述，直線MN的斜率為定值.

如果直線斜率結構比較復雜，可先不急著將斜率的內容代入直線，而是掛著斜率k算出交點坐標，然后再將斜率具體的內容代入坐標化簡.