一道高考試題的探究與溯源

黃旭東

(湖北省黃石市第一中學 435000)

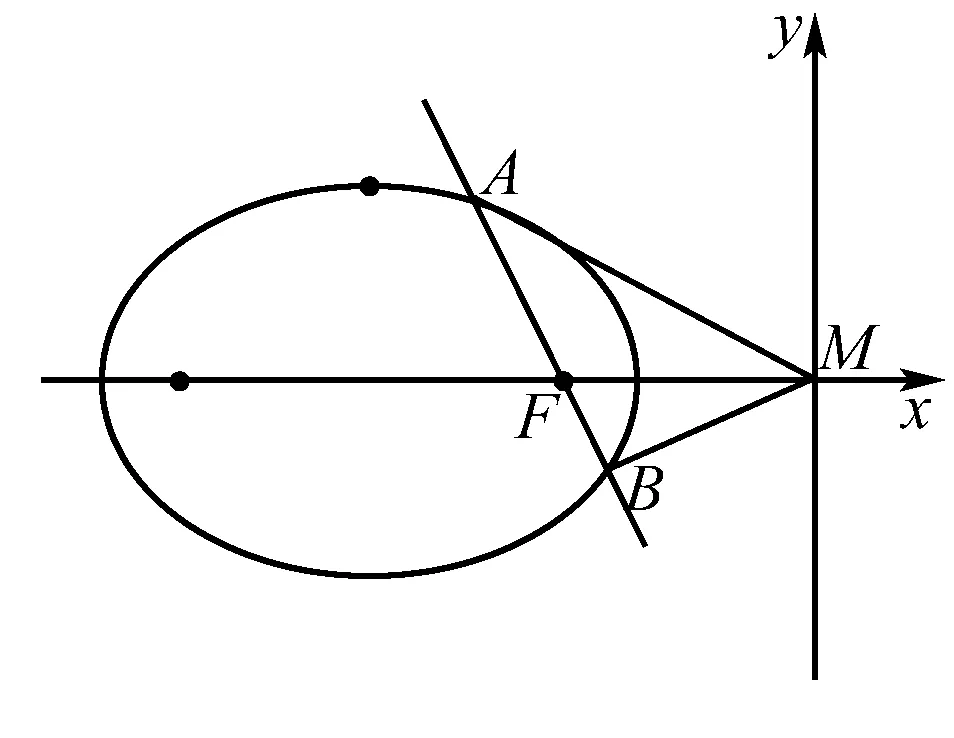
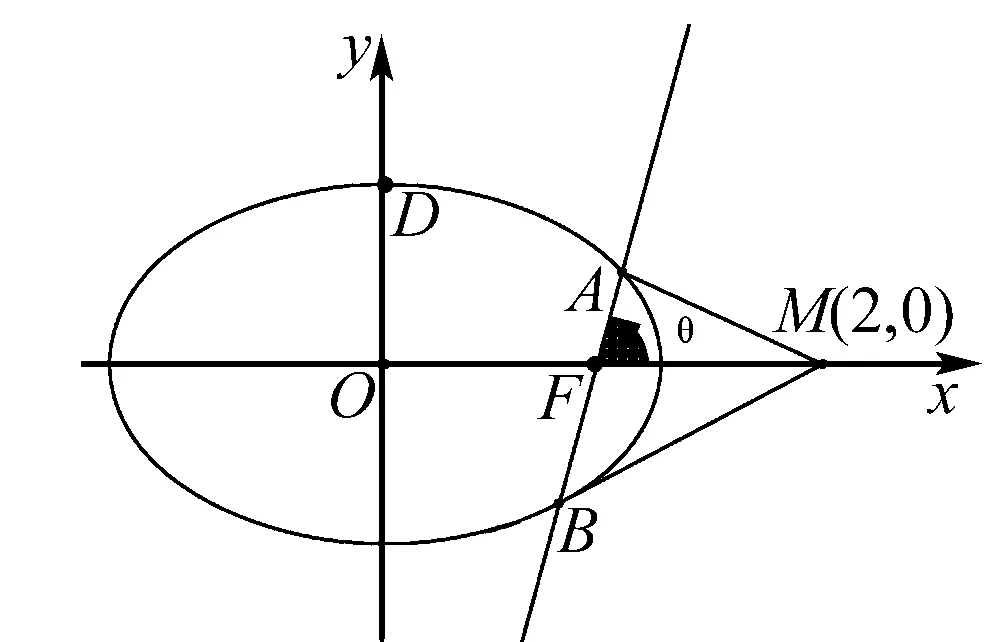
一、試題呈現(2018年新課標1中20題)

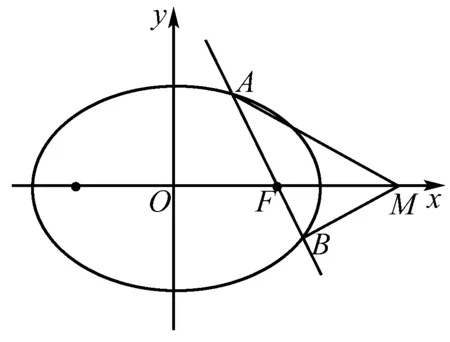
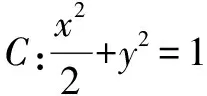
二、試題探究

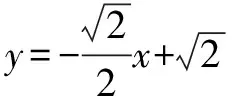
(2)(官方解答)當l與x軸重合時，∠OMA=∠OMB=0°;

當l與x軸時垂直時，OM為AB的垂直平分線，所以∠OMA=∠OMB.

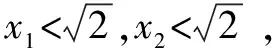
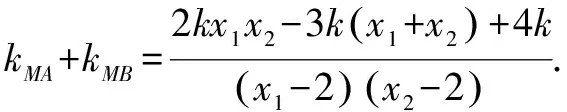
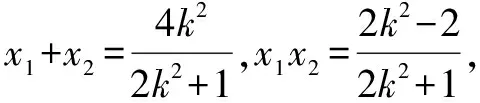
對(2)下面從不同的視角進行探究，作出幾種不同解答.

視角一 考慮到若將坐標系坐標原點平移到M點，則計算kMA+kMB時，利用韋達定理可較快計算出結果，可大大簡化運算.要說明的是這種方法是對方法一的改進.

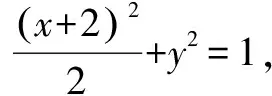
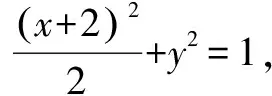
故MA，MB的傾斜角互補，所以∠OMA=∠OMB.

視角二 要證∠OMA=∠OMB，考慮點A關于x軸對稱點A′ ,則必有A′,B,M三點共線即可.

法2 (利用軸軸對稱，證明三點共線)

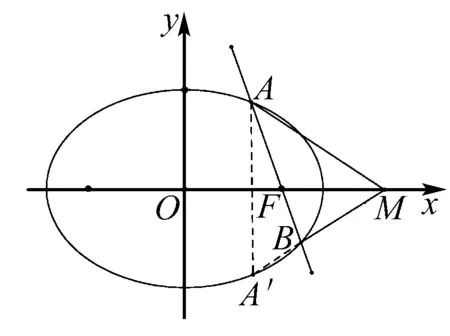
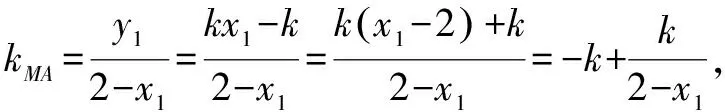
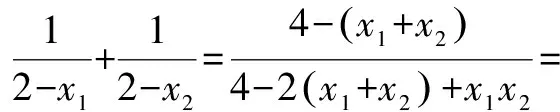
則kMA′=kMB，故M,A′,B三點共線.由于A(x1,y1)關于x軸對稱點A′(x1,-y1),則∠OMA=∠OMB

視角三 巧妙構建過定點M(2，0)的二次齊次式，處理斜率問題.

法3 當l與x軸重合時，∠OMA=∠OMB=0°.

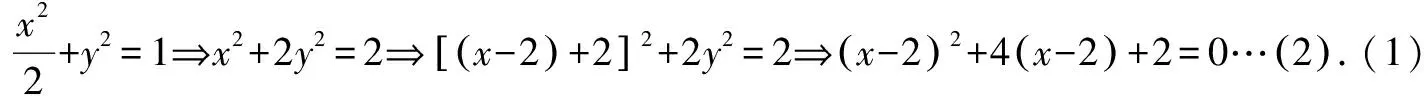
視角四 考慮角平分線性質，結合極坐標工具，可化成極坐標求解.

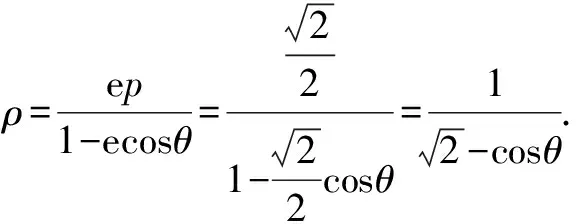
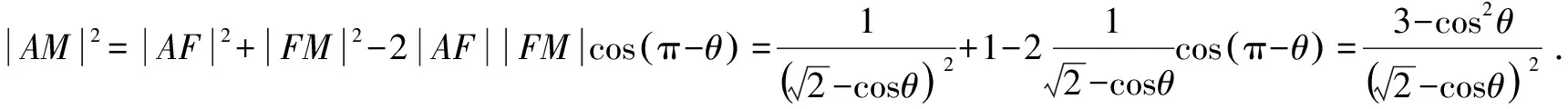
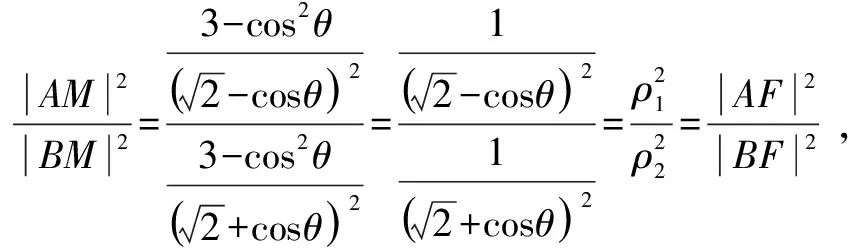
視角五 考慮角平分線性質，結合參數方程工具，可利用參數求解

法5 設直線l傾斜角為θ，則直線l的參數方程為

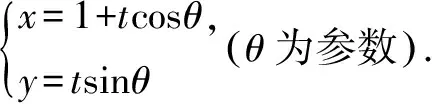
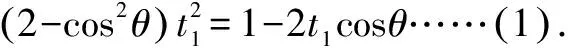
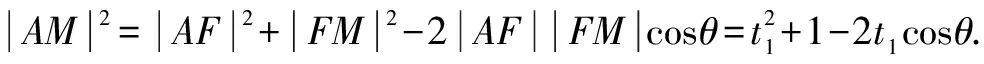
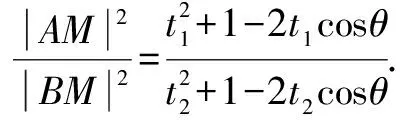
三、試題溯源

本題來源于下面定理

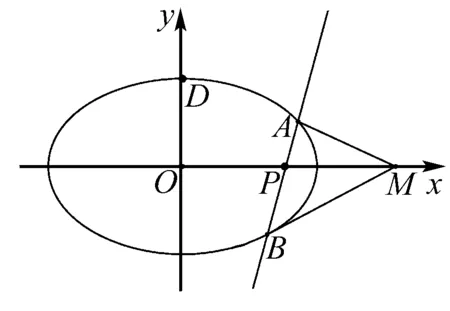
證明過程同上面方法相似，限于篇幅，此處略.同理類似上述性質可推廣到雙曲線與拋物線，即有：

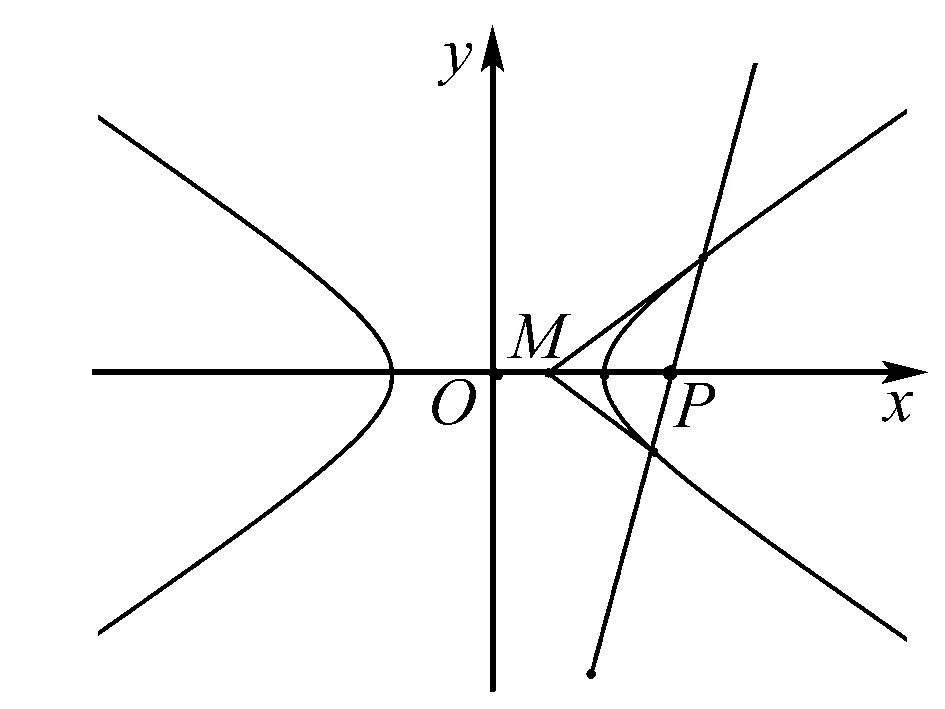
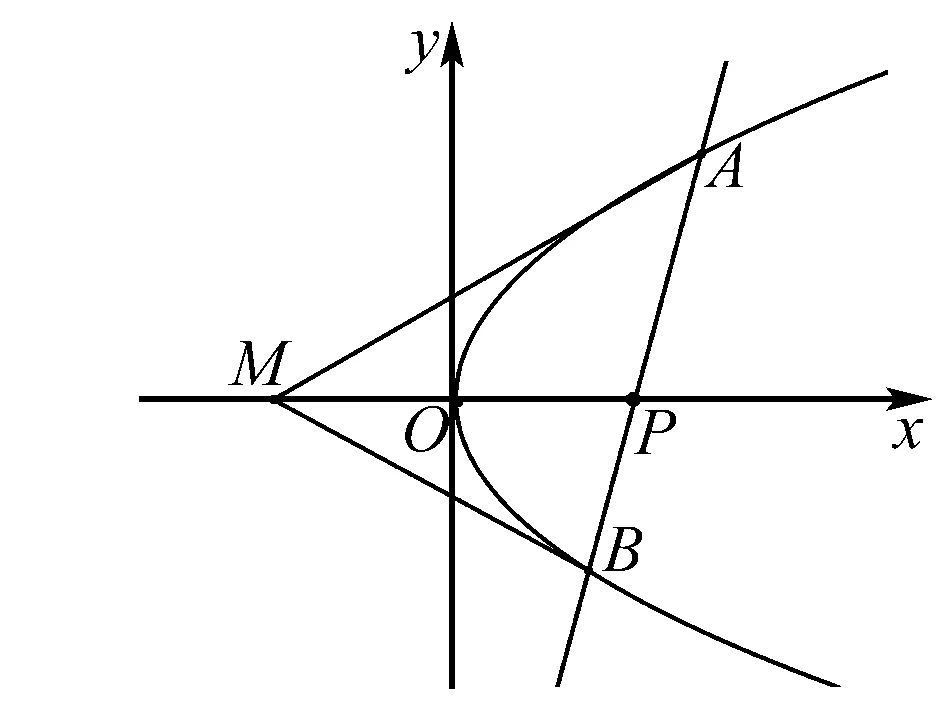
定理3 設拋物線：C：y2=2px(p>0),直線l過點P(t,0)與C交于A,B兩點，點M的坐標為(-m，0) 則有∠OMA=∠OMB.