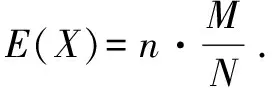超幾何分布與二項分布的錯解和正解的數學期望值相等

武增明

(云南省玉溪第一中學 653100)

一、問題的由來

在我校2017屆數學模擬考試中有兩道涉及超幾何分布與二項分布的概率題目，學生做得很不理想.具體題目如下：

1.為了解今年某校高三畢業班準備報考飛行員學生的體重情況，將所得的數據整理后，畫出了頻率分布直方圖(如圖1)，已知圖中從左到右的前3個小組的頻率之比為1∶2∶3，其中第2小組的頻數為4.

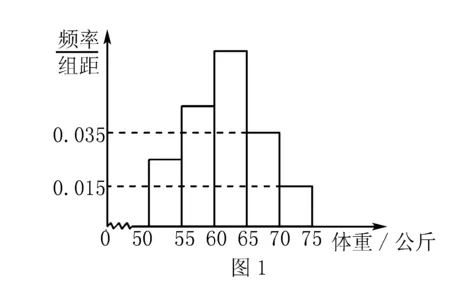
(1)求該校報考飛行員的總人數；

(2)以這所學校的樣本數據來估計全省的總體數據，若從全省報考飛行員的同學中(人數很多)任選3人，設X表示體重超過60公斤的學生人數，求X的分布列和數學期望.

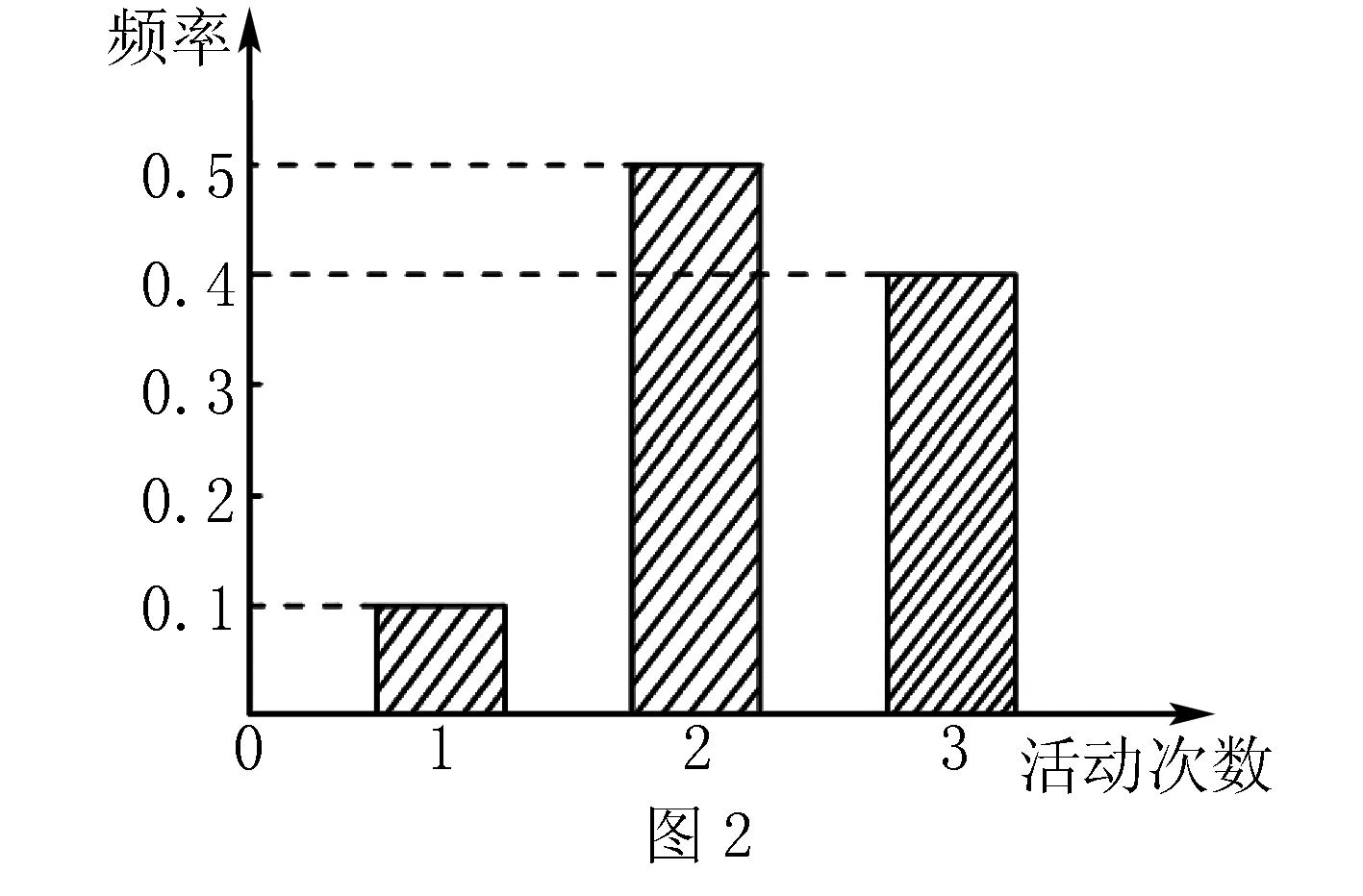
2.某中學動員學生在2017年春節期間至少參加一次社會公益活動(下面簡稱為“活動”).該校合唱團共有100名學生，他們參加活動的次數統計如圖2所示.

(1)求合唱團學生參加活動的人均次數；

(2)從合唱團中任選2名學生，求他們參加活動次數恰好相等的概率；

(3)從合唱團中任選2名學生，用ξ表示這兩人參加活動次數之差的絕對值，求隨機變量ξ的分布列及數學期望Eξ.

不少學生在解答這兩題的最后一問時出現了如下的典型錯誤：

1.(2)錯解 由題知，體重在60公斤以下的有6人，60公斤以上的有10人.隨機變量X服從超幾何分布且可以取：0，1，2，3.

2.(3)錯解 由題知，在每次抽取中，抽到參加1次、2次、3次活動的概率分別為0.1，0.5，0.4；

隨機變量ξ的取值為0，1，2.

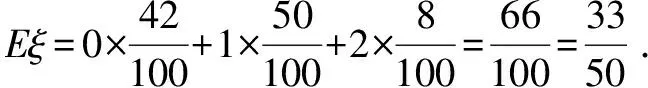
為了便于說明問題，我們給出兩題的正確解答.

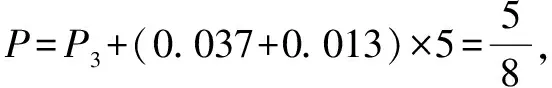
所以X服從二項分布，

隨機變量X的分布列為：

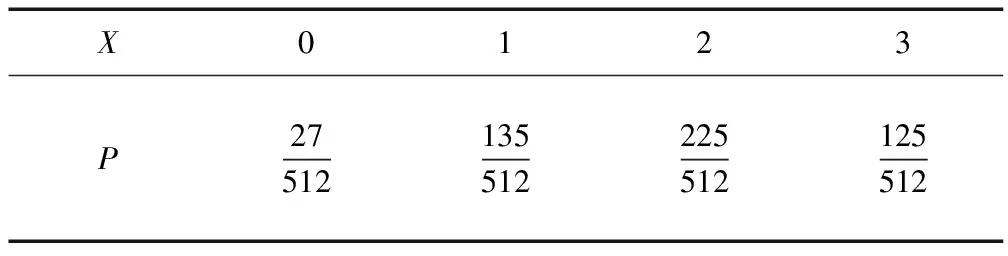
X0123P27512135512225512125512

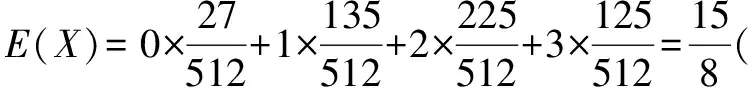
2.3正解 隨機變量ξ的取值為0，1，2，

ξ的分布列為：

ξ012P41995099899

數學期望

反思上述兩題中學生所犯的典型錯誤，我覺得我們需要思考為什么正解與錯解中的數學期望值相等這個問題.

二、問題的解決

超幾何分布定義(普通高中課程標準實驗教科書，數學2-3(A)，2009年4月第3版)：

X01…mPC0MCn-0N-MCnNC1MCn-1N-MCnN…CmMCn-mN-MCnN

為超幾何分布列，稱隨機變量X服從超幾何分布.

依數學期望的定義公式有：

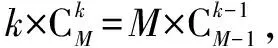
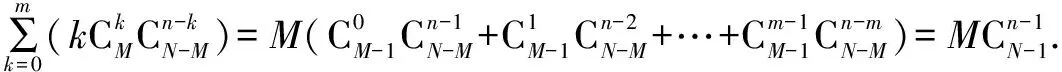
故超幾何分布與二項分布的錯解和正解的數學期望值相等.