數形結合思維與高中物理解題教學的融合分析

徐建平

(江蘇省贛榆第一中學 222100)

在高中物理教學中，教師曾提過很多種解題方法，也曾向我們驗證過方法的具體操作過程，如順序觀察法、理順制約關系及循因導果等，這些方法在實際解題過程中都展現出了非常有效的作用.但整合以往解題經驗可以發現，不管是哪種解題方法都可以從數形結合的思維入手進行分析.下面對數學結合思維在高中物理解題教學中的應用進行深層研究.

一、高中物理與數形結合

1.高中物理教學特點

對比初中時期學習的物理知識，高中物理看起來更加抽象和理論.在教師看來，物理學屬于定量的科學，物理學中的事物和事物之間的關系可以 依據代數式來展現，且不管我們是否可以感受到事物間的客觀形態，都能依據某種“形態”體現出來，因此在解決不同類型的物理問題時，都可以引用數形結合的思維進行研究.

2.數學結合概念分析

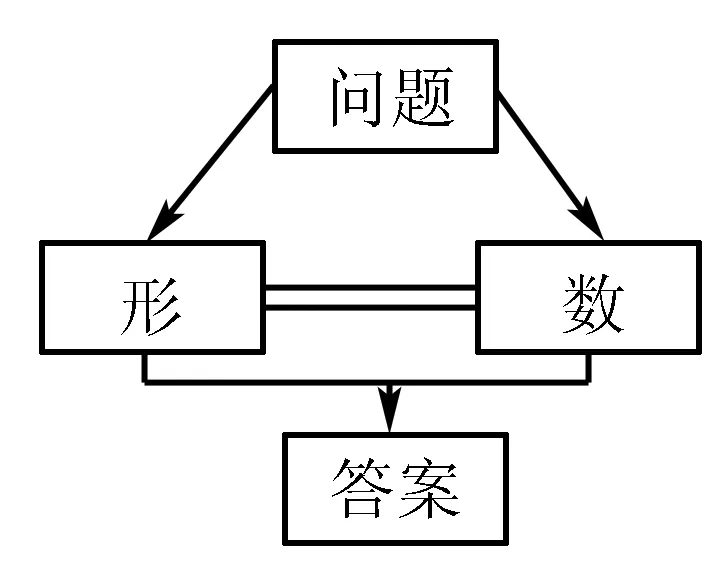
其源自于數學兩種基本要素“數”和“形”的結合.在“數”和“形”的整合研究中，可以讓問題變得更加簡單.從廣義角度分析，“數”和“形”屬于辯證統一的問題，數形結合思想可以引用到所有課程中.在解決問題的過程中，用代數式來精確表達問題，也可以通過圖形圖像來直觀表達，兩者優勢互補，可以讓解題變得非常簡單.具體解題形式如圖所示.

二、數形結合思維在高中物理解題中適用的題型

1.圖形選擇題

選擇題是高中物理解題教學的基礎，也是依據數形結合思維解題的常見類型.一般情況下，選擇題會為學生提供已知的圖像，促使學生可以在研究圖像的基礎上進行思考，并選擇正確的內容.在這類問題中，學生需要結合題干中給的已知條件，繪制正確的圖像，并結合所繪圖像與ABCD四個選項進行對比分析，排除錯誤答案，選擇正確選項.了解實踐案例可知，在高中物理選擇題中推廣數形結合思維，不但可以讓學生依據轉變急死俺獲取所需物理量，而且可以幫助學生結合各個物理量構建正確的圖像關系，進而明確更多的未知數.

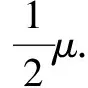
A.在F<2μmg時，A、B都相對地面靜止

C.在F大于3μmg時，A相對B滑動

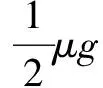
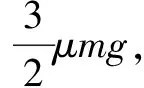
2.畫圖題

這類問題和選擇題都屬于結合物理量間的關系畫出正確的圖像，但后者可以讓學生通過對比分析排除錯誤選項，縮小正確答案的范圍.作圖題通常情況下不會給學生提示，需要他們在明確已知條件的基礎上，分析各個物理量間的關系，而后計算圖形中其他參數和面積，并畫出橫縱坐標，確定圖像中橫縱坐標代表的物理量，了解圖像中物理量的正負含義.同時，還要研究不同階段函數形式的圖線代表的物理過程，明確圖像的物理含義，而后引用對應的物理公式、理論等內容進行深層探索.在對物理圖像實施定量計算時，學生要認識到圖像展現的各個物理量間的函數關系，而后明確圖像中隱藏的條件關系，標出圖像中包含的各類信息，判斷橫縱軸上的截距代表的物理意義，并引用對應的物理規律實施計算.

例2 (多選)如圖2(a)所示，以物塊在t=0時刻滑上固定斜面，其運動的v-t圖線如圖2(b)所示，如果重力加速度及圖中的v0、v1、t1都是已知量，那么可以求出( ).

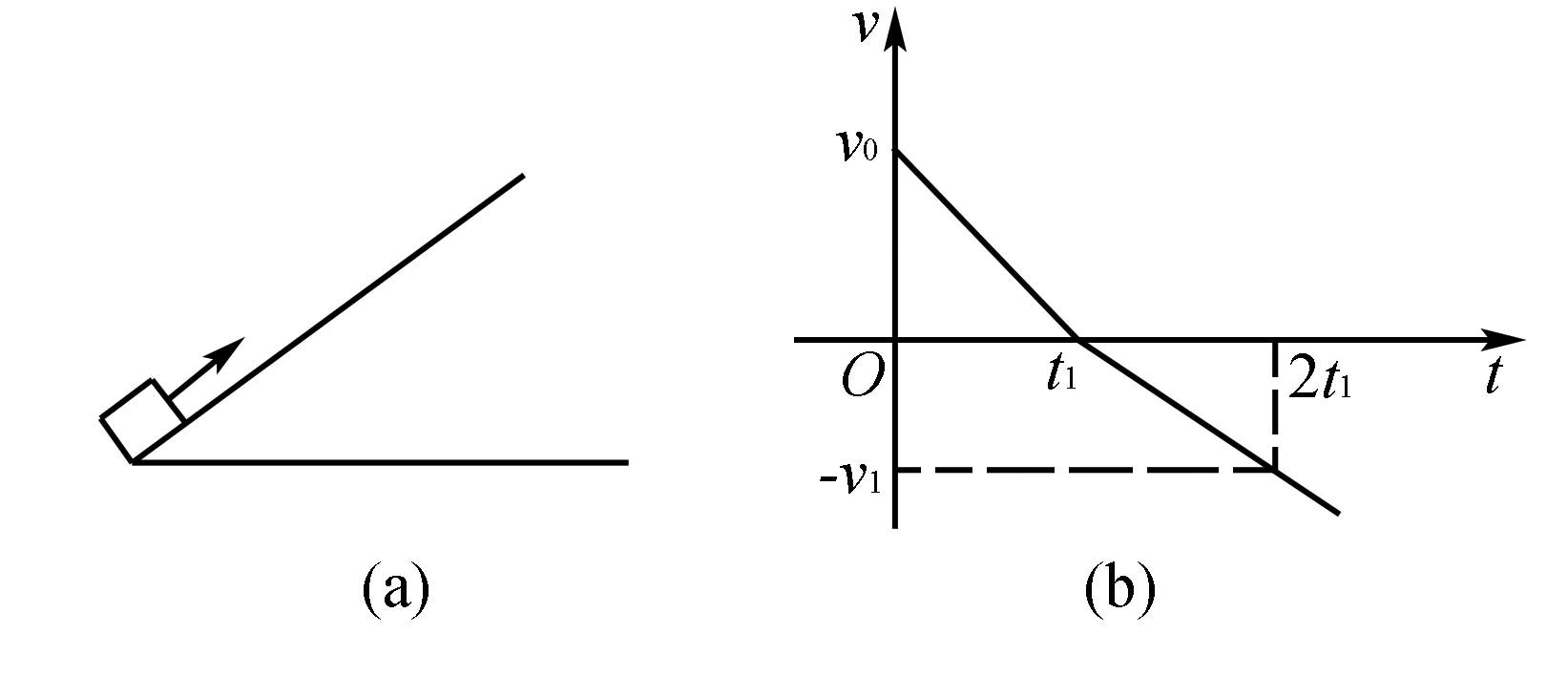
圖2

A.斜面的斜角

B.物塊的質量

C.物塊與斜面間的動摩擦因數

D.物塊巖斜面向上滑行的最大高度

解析 由圖2(b)可知，物體先向上減速到達最高時再向下加速；圖象與時間軸圍成的面積為物體經過的位移，故可求出物體在斜面上的位移；圖象的斜率表示加速度，上升過程及下降過程加速度均可求，上升過程有：mgsinθ+μmgcosθ=ma1；下降過程有：mgsinθ﹣μmgcosθ=ma2；兩式聯立可求得斜面傾角及動摩擦因數；但由于m均消去，故無法求得質量；因已知上升位移及夾角，則可求得上升的最大高度；故選：ACD．

3.圖形轉換題

這類問題屬于高中物理解題時引用數形結合思維的另一經典題型.了解以往高中物理習題類型可知，很多圖像看起來沒有規律，但學生若是可以合理引用數形結合思想進行研究，促使物理圖形轉變為函數圖像，就可以獲取新的解題思路，這對提升解題效率和質量而言具有積極作用.在新課改教學理念提出，教師不但要引導學生熟練掌握所學理論知識，而且要熟練引用所學知識解決現實問題，只有這樣才能促使學生全面發展，由此數形結合思維在圖形轉換題中的應用至關重要.

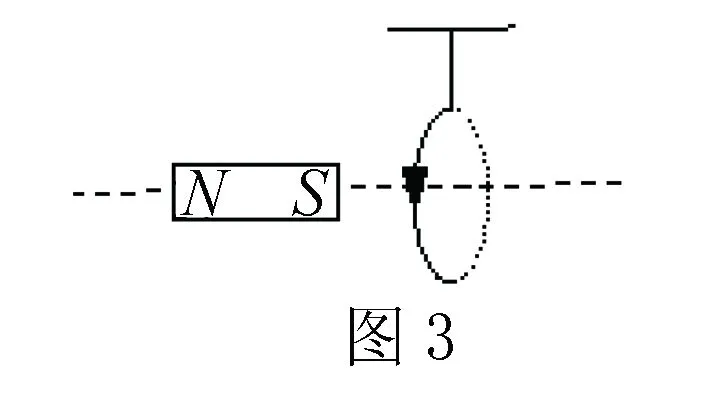
例 如圖3所示，將輕質導線依據絕緣細線懸掛在磁鐵S周邊，磁鐵的軸線穿過線圈平面，在線圈通過如圖所示的方向電流時，線圈是如何運動的？

解析 在本題中，要想判斷線圈是如何運動，最重要的依據左手定則研究，在條形磁鐵感線中線圈所受的安培力.我們可以結合通電線圈磁感線和條形磁鐵相似.將通電線圈轉化為條形磁鐵，具體如下圖4所示.或者是將條形磁鐵轉變為線圈，具體如圖5所示.由此，可以判斷出線圈向右偏.

綜上所述，在物理解題過程中，依據數形結合的思想解決物理問題，一定要結合具體情況選擇適宜的數形結合方法，以抽象、復雜化的物理圖形問題為例，學生可以選擇“形”的數解方式進行操作.又如在解決各數關系過于繁瑣的物理問題時，選擇可以選擇“數”的型化方法進行解決，以此在優化學生物理解題能力的基礎上，拓展他們的思維空間.