直線與方程快樂導學王佩其

■王佩其

同學們，你一定見過斜拉橋，斜拉橋的拉索可以看成方向不同的一些直線。實際生活中，如何來刻畫直線的傾斜程度呢?要弄清這個問題，我們必須先學習直線與方程。

一、知識要點梳理

1.直線的傾斜角

(1)當直線l與x軸相交時，取x軸作為基準，x軸正向與直線l向上方向之間所成的角叫作直線l的傾斜角。當直線l與x軸平行或重合時，規定它的傾斜角為0°。

(2)直線l傾斜角的范圍是[0°，180°)。

2.斜率公式

(1)若直線l的傾斜角α≠90°，則斜率k=tanα。

(2)若點P1(x1，y1)，P2(x2，y2)在直線l上且x1≠x2，則直線l的斜率

3.直線方程的五種形式

(1)點斜式的適用范圍是不含直線x=x0。

(2)斜截式的適用范圍是不含垂直于x軸的直線。

(3)兩點式的適用范圍是不含直線x=x1(x1≠x2)和直線y=y1(y1≠y2)。

(4)截距式的適用范圍是不含垂直于坐標軸和過原點的直線。

(5)一般式的適用范圍是平面直角坐標系內的所有直線。

4.兩條直線的位置關系

(1)兩條直線的位置關系有平行，垂直和相交。兩條不重合的直線l1，l2，若其斜率分別為k1，k2，則l1∥l2?k1=k2。當直線l1，l2不重合且斜率都不存在時，l1∥l2。

(2)如果兩條直線l1，l2的斜率存在，設為k1，k2，則l1⊥l2?k1·k2=-1。當其中一條直線的斜率不存在，而另一條直線的斜率為0時，l1⊥l2。

(3)直線l1與l2的交點坐標就是兩條直線方程組成的方程組的解。

二、典型例題剖析

例1已知坐標平面內的三點A(-1，1)，B(1，1)，C(2，3+1)。

(1)求直線AB，BC，AC的斜率和傾斜角。

(2)若D為△ABC的邊AB上一動點，求直線CD的斜率k的取值范圍。

解：(1)由斜率公式得0，即得直線AB的傾斜角為0°。

(2)在平面直角坐標系中，作出直線AB，BC，AC，如圖1所示。

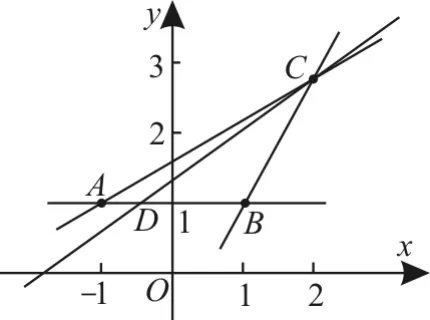
圖1

由圖像可知，當斜率k變化時，直線CD繞點C旋轉，當直線CD由CA沿逆時針方向旋轉到CB位置時，直線CD與AB恒有交點，即點D在△ABC的邊AB上，此時斜率k由kCA增大到kCB，所以斜率k的取值范圍為。

由傾斜角(或范圍)求斜率(或范圍)，可利用定義式k=tanα(α≠90°)來解決。由兩點坐標求斜率，可利用斜率公式求解。涉及直線與線段有交點問題時，可利用數形結合法求解。

例2已知兩條直線l1∶ax-by+4=0和l2∶(a-1)x+y+b=0，求滿足下列條件的a，b的值。

(1)l1⊥l2，且l1過點(-3，-1)。

(2)l1∥l2，且坐標原點到這兩條直線的距離相等。

解：(1)由題意可知l2的斜率存在，且k2=1-a。

若k2=0，則1-a=0，即a=1。

因為l1⊥l2，所以直線l1的斜率k1必不存在，即b=0。又因為l1過點(-3，-1)，所以-3a+4=0，即(與a=1矛盾)，可知此種情況不存在，故k2≠0，即k1，k2都存在且不為0。

因為l1⊥l2，所以k1k2=-1，即a)=-1。 ①

又因為l1過點(-3，-1)，所以-3a+b+4=0。 ②

由①②解得a=2，b=2。

(2)因為直線l2的斜率存在，l1∥l2，所以直線l1的斜率存在，可知k1=k2，可得=1-a。 ③

又因為坐標原點到這兩條直線的距離相等，且l1∥l2，所以l1，l2在y軸上的截距互為相反數，即

當直線方程中存在字母參數時，不僅要考慮斜率存在的一般情況，也要考慮斜率不存在的特殊情況，同時還要注意x，y的系數不能同時為零這一隱含條件。在判斷兩條直線平行或垂直時，也可直接利用直線方程的系數間的關系得出結論。

例3若直線l過點P(-1，2)且到點A(2，3)和點B(-4，5)的距離相等，則直線l的方程為

解：(方法1)當直線l的斜率存在時，設直線l的方程為y-2=k(x+1)，即kxy+k+2=0。由題意知，即|3k-1|=|-3k-3|，所以所以直線l的方程為y-2=，即x+3y-5=0。

當直線l的斜率不存在時，直線l的方程為x=-1，也符合題意。

故所求直線l的方程為x+3y-5=0或x=-1。

(方法2)當線段AB∥l時，可得kl=，這時直線l的方程為y-2=，即x+3y-5=0。

當l過線段AB的中點時，由線段AB的中點為(-1，4)，可得直線l的方程為x=-1。

故所求直線l的方程為x+3y-5=0或x=-1。

利用距離公式應注意的是∶①點 P(x0，y0)到直線x=a的距離d=|x0-a|，到直線y=b的距離d=|y0-b|;②應用兩平行線間的距離公式時，要把兩直線方程中x，y的系數化為相同的系數。