以一道課本習題為例談阿波羅尼斯圓

■甘大旺

人教A版高中數學②的第124頁習題4.1B組第3題∶已知點M與兩個定點O(0，0)，A(3，0)的距離的比為1∶2，求點M的軌跡方程。

解法1：設動點M的坐標是(x，y)，則依題意得整理得x2+y2+2x-3=0。經檢驗，點M的軌跡方程是(x+1)2+y2=4。

解法2：①當點M在直線OA上時，由于，則動點M恰有兩個位置M(1，10)，M2(-3，0)適合②當點M不在直線OA上時，由于，則 MM、MM分別是∠OMA 的12內、外角平分線，故MM1⊥MM2，則M在以M1M2為直徑的圓上。

由①②可知，點M的軌跡是以線段M1M2的中點O'(-1，0)為圓心，以為半徑的圓(如圖1所示)，所以點M的軌跡方程是(x+1)2+y2=4。

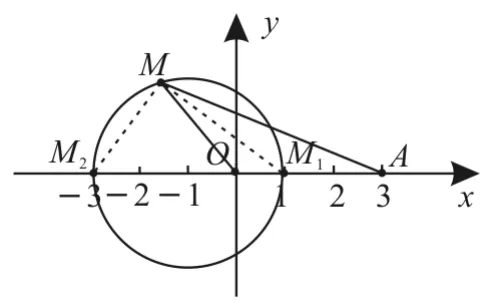
圖1

反思：解法1運用直接求軌跡法，簡潔快速;解法2運用幾何求軌跡法，雖然解題過程稍長，但卻能夠自然而然地引導我們揭示這道課本習題的數學史背景——阿波羅尼斯圓。阿波羅尼斯是古希臘亞歷山大早期的三大數學家之一(前兩位是歐幾里得和阿基米德)，僅憑一部巨著《圓錐曲線論》就使得古希臘幾何學在世界數學史上登峰造極，而至少領先1500年。阿波羅尼斯發現了一個流傳至今的結論∶“平面上到兩個定點的距離之比等于定值(且該定值不為1)的動點軌跡是一個圓”。后來，數學界把這個圓稱為阿波羅尼斯圓。

探索：在共線的順次四點 M1(1，0)，M2(-3，0)，O(0，0)，A(3，0)中，已有等式，驗證知由此我們可知，到兩點M，1M2的距離之比為1∶3的動點N的軌跡方程是以線段OA為直徑的圓，故圓的方程為(如圖2所示)。

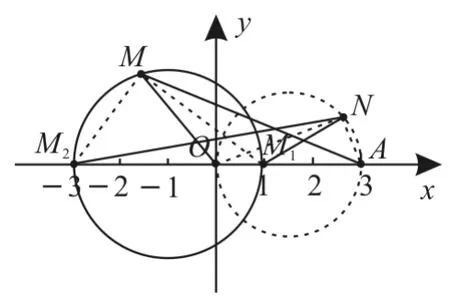
圖2

發現：抽象思考上述解法2，嘗試探索，不難提煉出一個概括結論，即定理1。

定理1：已知平面內在同一條直線上的順次四點A，P，B，Q滿足兩個等式

(1)在該平面內到兩點A，B的距離之比等于定值λ的動點M的軌跡是以線段PQ為直徑的阿波羅尼斯圓。

(2)在該平面內到兩點P，Q的距離之比等于定值μ的動點N的軌跡是以線段AB為直徑的阿波羅尼斯圓。

驗證：(1)(2)類似于上述解法2(過程略)。(3)如圖3，不妨設四點A，P，B，Q順次在x軸上，并用一維坐標分別標記為A(0)，P(p)，B(b)，Q(q)，由于λ，則，即(等比定理)(合分比定理，反比定理)，則，故解得

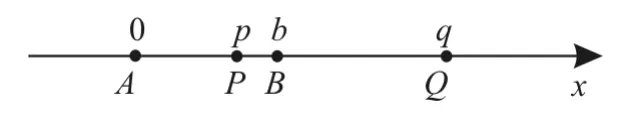
圖3

定理1中的(1)(2)蘊含著兩個相伴阿波羅尼斯圓的直徑畫法;反之，平面上任意兩個相交圓是不是這種相伴的阿波羅尼斯圓呢?定理1中(3)的比值范圍給予了否定。

除上述例題外，人教A版高中數學②還有兩道涉及阿波羅尼斯圓的習題，分別是第4.3節140頁“信息技術應用”的例題，144頁第4章復習參考題的B組第2題。

下面再提供兩道相關的跟蹤練習題。

跟蹤練習1：在△ABC中，AB=2AC，角A的平分線AD交BC于點D，且AD=kAC，△ABC的面積等于1，問∶當k為何值時BC最短?

審題方法：點D以分比為2內分線段BC，作其外分點E，則到兩點B，C的距離之比等于定值2的動點A在以線段DE為直徑的阿波羅尼斯圓上。

解題思路：單純著眼于三角形的邊角關系，可以選用三角法;著眼于轉化為阿波羅尼斯圓問題，可以選用解析法。

解法1：根據cos∠CAB=cos2∠CAD，BD=2BC，運用余弦定理解答(過程略)。

解法2：依題意，記AB=2AC=2b，AD=kAC=kb。根據三角形的內角平分線定理，得則AD=2DC以分比作線段BC的外分點E，則到兩點B，C的距離之比等于定值2的動點A在以線段DE為直徑的阿波羅尼斯圓上，如圖4所示。

圖4

再取該阿波羅尼斯圓的圓心O為原點，直線BE為x軸，建立平面直角坐標系xOy，則該阿波羅尼斯圓O的方程是x2+y2=依題意得則，代入圓O的方程得0，解得a2≥3。驗證知當xA=0時，BC=a取最小值 3，此時，OA⊥DE，則所以，當時，BC最短。

變式訓練1：已知點P到兩個定點M(-1，0)，N(1，0)的距離之比為 2，點 N到直線PM的距離為1，求直線PN的方程。

提示：到兩個定點M(-1，0)，N(1，0)的距離之比為2的阿波羅尼斯圓是(x-3)2+y2=8，直線PM的傾斜角為30°或150°，求得直線PN的方程是x±y-1=0。

變式訓練2：正方形ABCD內部的一點P滿足AP∶BP∶CP=1∶2∶3，求∠APB。

提示：先用阿波羅尼斯圓方程，后用余弦定理，也可單獨用余弦定理，不妨設正方形的邊長為1，最后求得∠APB=135°。

跟蹤練習2：已知兩點A(-2，0)，B(2，0)，點P滿足，且PB⊥AB。試在x軸上尋找一點M，使得AP⊥PM。

審題方法：點P在到兩點A，B的距離之比等于定值3的阿波羅尼斯圓上，考慮已知直角∠ABP=90°和目標直角∠APM=90°。

解題思路：把零散條件拼湊起來，運用方程組解答;巧妙轉化，運用阿波羅尼斯圓。

解法1：設點M為(m，0)，解方程組(過程略)。

解法2：在直線AB上以分比λ=3找到線段AB的內分點P1(1，0)，P2(4，0)，則點P在阿波羅尼斯圓上，且滿足PB⊥AB，如圖5所示，該圓的圓心為。設點M為(m，0)，使得AP⊥PM，則由直角三角形中的射影定理，得即(-2)]·(m-2)，化簡得2=4(m-2)，解得所以在x軸上尋找到的點M為，符合題意。

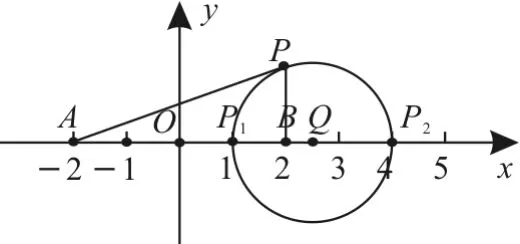
圖5

發現：這里求出的點M重合于圓心，于是我們又可以提煉出一個概括結論，即定理2。

定理2：在平面上，線段AB以定值λ(大于1)為分比的內外分點分別為P1，P2，以線段P1P2為直徑作阿波羅尼斯圓Q，作該圓Q的弦P3P4，則連線AP3，AP4是圓Q的兩條切線。

變式訓練3：驗證定理2。

提示：可用解析法，用到定比分點坐標公式(過程略)。

變式訓練4：如圖6，過點A(-2，-1)作圓Q∶(x-2)2+(y-1)2=4的兩條切線AT1，AT2，切點弦T1T2與連線AQ交于點H，圓Q與連線AQ交于點B，C，連接T2C。

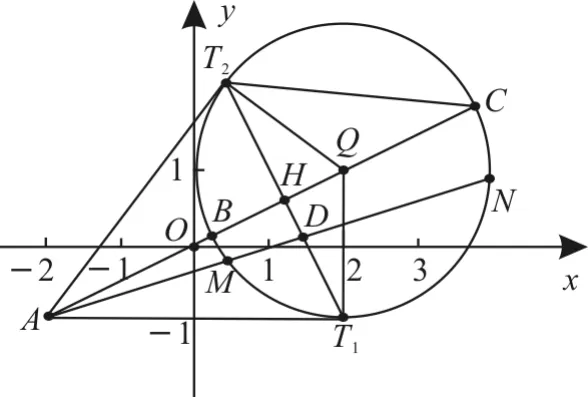
圖6

(1)求證∶T2C是∠AT2H的外角平分線。

(3)過點A作圓Q的割線與圓Q交于點M，N，與切點弦T1T2交于點D，試探究等式是否恒成立。

提示：則所以故TC是∠ATH的外角平分線。

(3)設割線MN的點斜式方程為y+1=k(x+2)，與圓Q的方程聯立，消去y并整理成關于x的二次方程，用到韋達定理。T1T2⊥AQ，可求出連線T１T２的12方程是2x+y-3=0。由等式(xM+xN)+2·xMxN=4·xD。代入檢驗，等式恒成立。

說明：定理、跟蹤練習與變式訓練不但以阿波羅尼斯圓為數學史背景，同時還孕育著極點、極線、調和點列的萌芽，同學們在學習之余請多思考這幾道題的特點。