關注學生發展 實施單元教學

沈華

[摘? 要] “單元教學”“關注初中生學力發展”都源于李庾南老師的“自學·議論·引導”教學法，是指基于學生已有的基礎，以提升學生學力為宗旨，打破按課時分配的小段教學，對學材進行加工、重組，靈活組織單元教學內容的教學方法. 將單元教學與學生發展需求相結合，這是我校近期深入探究的一項課題.

[關鍵詞] 單元教學;學生發展需求;初三復習課;三角形

數學知識的教學，要關注知識的“生長點”和“延伸點”，把每節課的教學內容放在整體知識體系中，注重知識的結構與體系，處理好局部知識和整體知識的關系，引導學生感知數學知識的整體性[1]. 課程標準指導我們一線教師在教學過程中要考慮知識的整體性，不要把某些整體的知識碎片化，要實施單元教學. 在實施單元教學時，不僅要考慮對教材內容的有機整合，也要考慮學生的發展需求，教學過程就是在教師的引導下，不斷地將學生的“最近發展區”轉化為現有的發展水平，向潛在的發展水平提升，是一種螺旋式發展的過程[2]. 筆者參加海門市初三復習課研討活動，并執教了人教版初三復習課“三角形”，嘗試立足于學生發展需求，通過單元教學，整合初中數學有關三角形的知識（三角形的邊、角、勾股定理、銳角三角函數、等腰三角形，以及全等三角形、相似三角形的關系），整體理解三角形相關知識，力爭取得較好的教學效果.

教學流程及設計意圖

1. 通過運算，弄清基礎知識

師：今天我們研究的“對象”是三角形，它有哪些基本元素？

生：線段、角，其中三角形中的線段包括三角形的邊及三條重要線段：中線、角平分線、高線.

今天我們就從三角形的邊、角出發，逐漸增加其條件，豐富其情節，復習與三角形有關的知識.

活動一：算一算

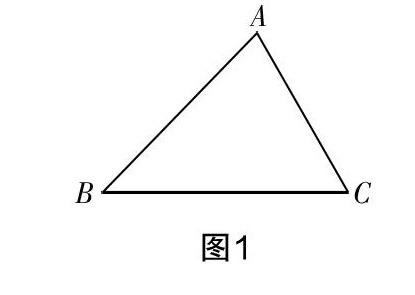
問題：如圖1，在△ABC中，∠A=70°，你能求出∠B的度數嗎？若不能的話，你能添加一個條件，求出∠B的度數嗎？你有哪些不同的方法？

[圖1]

生1：只給出一個條件∠A=70°，只能得到∠B+∠C=110°，而不能得出∠B的度數.

生2：增加一個條件，如“∠C的度數為60°”，利用三角形的內角和得∠B=180°-70°-60°=50°;或者增加“∠C的外角=120°”這一條件，利用外角等于和它不相鄰的兩個內角的和來求出∠B的度數.

生3：增加一個條件是∠B與∠C的數量關系，如“∠C=3∠B”，由已知條件得∠B+∠C=110°，這樣得到關于∠B，∠C的方程組，從而求出∠B.

生4：增加一個條件是“△ABC為等腰三角形”，這樣要分情況討論：若∠A為頂角，則∠B=（180-70）÷2=55°;若∠A為底角時，∠B為底角的話，∠B=∠A=70°;∠B為頂角的話，則∠C為底角=70°，∠B=180-70-70=40°.

師追問：若∠A=100°呢？

生5：∠A為鈍角，只能作為等腰三角形的頂角，故只有一種情況，∠B=（180-100）÷2=40°.

生6：增加一個條件是“△ABC為直角三角形”，這樣也要分情況討論：∠B若為直角，則∠B=90°;若∠C為直角，則∠B=90-70°=20°.

設計意圖? 基于學生已有的基礎，特別是數學基礎較薄弱的學生，設置低起點的問題，以激發所有學生學習的積極性. 通過以簡單問題為引導，設計開放型問題，學生獨立思考，個別回答，其余學生補充，教師適時追問等形式，讓學生弄清利用三角形的內角和定理來解決一般三角形、等腰三角形、直角三角形中有關角的計算，總結出分類討論、方程思想等數學思想方法.

活動二：求一求

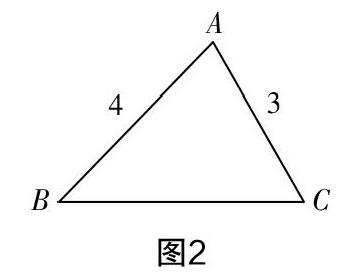
問題：如圖2，在△ABC中，AB=4，AC=3. BC邊的取值范圍為______;你能求出BC的長嗎？你能添加一個條件，求出BC的長度嗎？你有哪些不同的方法？

[圖2]

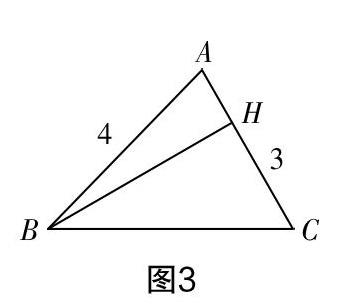
生7：求不出BC的長，但根據三角形的三邊關系，兩邊之和大于第三邊，兩邊之差小于第三邊，有4-3

生8：添加一個條件“∠A=90°”，則利用勾股定理得BC===5.

師追問：若條件改為△ABC為直角三角形呢？

生9：此時沒有明確哪個角是直角，所以要分類討論：當∠A為直角時，BC=5;當∠C為直角，則AB為斜邊，BC===;AC不是最大的邊，∠B不可能為直角，所以BC的長為5或.

生10：類比剛才老師的提問，可以添加一個條件“△ABC為等腰三角形”. 同樣要進行分類討論：若AB，BC為腰，則BC=4;若AC，BC為腰，則BC=3，所以BC=4或BC=3.

師追問：若△ABC為等腰三角形，條件改為AB=4，AC=2呢？

生11：同樣要進行分類討論：若AB，BC為腰，則BC=4;若AC，BC為腰，則出現AC+BC=2+2=4=AB，AB，AC，BC不能組成三角形，所以BC的值只能為4.

生12：添加一個條件“∠A=60°”. 作BH垂直AC于點H（如圖3），在Rt△ABH中，可得AH=2，BH=2，所以CH=AC-AH=3-2=1，在Rt△BCH中，利用勾股定理得BC===.

[圖3]

師追問：已知△ABC中，AB=4，AC=3.若添加的條件為∠B=30°，BC長度為多少呢？

生13：過點A作AH垂直于BC于點H（如圖4）， 在Rt△ABH中，可得AH=2，BH=2，在Rt△ACH中，利用勾股定理得CH===，所以BC=BH+CH=2+.

[圖4]

生14：還有一種情況，如圖5所示，此時BC=BH-CH=2-. 所以BC長為2+或2-.

[圖5]

設計意圖? 基于學生已有對三角形三邊關系、勾股定理、特殊角的三角函數等知識的掌握，通過條件開放以激發所有學生學習的積極性. 通過以開放型問題為引導，學生獨立思考，若有困難可進行小組交流討論，教師適時追問，變式等形式，讓學生弄清三角形中有關線段計算的常見類型，總結出通過作高，把一般三角形轉化為直角三角形的“化斜為直”的方法，以及三角形的高在形內和形外的“分類討論”思想.

2. 變式引領，拓展關聯知識

活動三：變一變

在△ABC中，AB=4，AC=3.

（1） 如圖6，AD為高，且AD=，則BC=______.

[圖6]

變式1：若還是這個條件，沒有給你圖，你會求BC的長嗎？

變式2：你會求三角形ABC的面積嗎？

變式3：求出某些角的三角函數值.

（2）如圖7，AD為三角形的中線，則S ∶ S=______;AD的取值范圍為______.

[圖7]

變式1：如圖7，取AC的中點E，連接BE，交AD于點O，連接DE，在這個圖中你能得到哪些有關三角形以及邊、角的結論？

變式2：若△ODE的面積為1，你能求出圖中哪些三角形的面積？

（3）如圖8，AD為角平分線.

[圖8]

①點D到AC，AB的距離是什么數量關系？

②S ∶ S=______.

變式1：若S=4，則是S=______.

變式2：BD ∶ AD=______.

設計意圖? 基于學生對三角形中重要的三條線段：高、中線、角平分線的理解與掌握，通過合理的變式，串聯起初中階段與之相關的知識點，化零碎為整體. 第（1）題以三角形的高有關問題為引導，復習三角形的面積、勾股定理、三角函數等相應知識，沒有明確高的位置，要分形內和形外，提煉出“分類討論”的思想. 第（2）題以三角形的中線有關的開放型問題為引導，弄清中線的定義，倍長中線構造全等三角形等常用方法. 通過變式1，復習三角形的中位線、相似、位似的定義、性質及應用，可以得出如DE ∶ AB，BO ∶ OE，AO ∶ OD，S ∶ S， S ∶ S 等結果;通過變式2，可以得出各三角形面積與底之比、高之比的關系. 第（3）題以三角形的角平分線有關的問題為引導，利用角平分線的性質，得出兩三角形高相等時，面積比等于底之比，變式2是在高相等時，底之比等于面積比.

3. 反思提升，構建知識結構

活動四：講一講

（1）體會本節課我們是以三角形的什么基本元素為基礎展開研究的？具體研究了三角形哪些內容？

（2）通過本節課的復習，你積累了哪些數學思想、數學方法？

設計意圖? 通過反思總結，學生說出本節課所研究的內容，師生共同搭建本節課的知識框架圖，使得初中階段與三角形有關的內容通過單元教學，清晰地呈現在師生面前，由零碎的知識點到網狀的知識框架圖，完成“由點到網”的學習過程.

教后反思

本節初三復習課的教學，不是傳統的用大量題目來回顧、復習相應的知識點，而是通過一個基本的三角形，知道某些角或邊的量，逐漸添加條件，通過變式、追問等形式，引導學生對相應知識進行回顧、鞏固以及綜合運用. 學生學力的生成、發展呈現出自主性、開放性、發展性、綜合性等特點[3]. 高效復習課應從以下角度思考，從而提高學生的學力.

1. 基于學生發展需求

學生發展需求是指學生在學習過程中提升自我能力的一種欲望. 這一欲望首先建立在已有知識的基礎上，教學時要基于學生已有的知識，低起點，緩坡度，螺旋式逐步漸進提升，這樣有利于培養學生思考問題的積極性，增強學生的自學能力，建立良好的認知結構，培養、發展數學思維方法和能力.

2. 精選例題，變式引領

初三的復習課，不同于普通章節的復習課，涉及的知識點多、雜，不能靠大量的題目來復習相應的知識點，例題的精選顯得尤為重要. 以例題為起點，帶動本節課的基礎知識點，通過條件開放、變式引領，讓學生有更多考慮問題的角度，充分發揮學生的主體作用，復習步步深入，達成本節課的復習目標.

3. 構建單元教學框架圖

初三復習課通過知識框架圖將相應的知識網狀化、系統化，讓學生對該單元知識的認識更深入、深刻，感知各個知識點不是零散的、孤立的，而是相互有聯系的，讓學生從整體視角下理解各知識點，有利于對知識的記憶，提高自身的數學能力.

總之，在初三數學復習教學中，一定要基于學生的發展需求，以學生為教學主體，精心設計例題，強化知識結構，在教師的引導下，最大限度地提高復習效率.

參考文獻：

[1]中華人民共和國教育部. 義務教育數學課程標準（2011年版）[M]. 北京：人民教育出版社，2012.

[2]李庾南. 自學·議論·引導教學論[M]. 北京：人民教育出版社，2013.

[3]李庾南，陳育斌. 中學數學新課程教學設計30例[M]. 北京：人民教育出版社，2007.