對高職數學函數極值和最值的教學過程研究

[摘 ? ? ? ? ? 要] ?函數極值是高等數學中一個重要的基本概念，是學習最值的重要基礎.通過直觀教學法、問題驅動法、案例教學法等設計教學過程，改進高職數學函數極值和最值的傳統教學過程，將函數的極值和最值統一進行教學。

[關 ? ?鍵 ? 詞] ?函數極值;駐點;極值點;最值

[中圖分類號] ?G712 ? ? ? ? ? ? ? ? [文獻標志碼] ?A ? ? ? ? ? ?[文章編號] ?2096-0603（2019）30-0062-02

一、前言

函數的極值是高等數學中一個重要的基本定義，作為初等函數的重要內容之一，它既是函數導數的進一步應用，又是學生后續學習函數最值的基礎.高職院校學生由于數學功底薄弱，深刻理解函數極值和應用往往存在一定的困難，尤其是函數極值點與駐點關系和實際問題中的最值問題.本文是在傳統教學基礎上采用直觀教學法、問題驅動法、類比法等多種教學方法設計教學過程.學生學習時采用探究式、自主式和合作式的學習方式，這樣的設計既有利于培養學生的數學思維，分析問題、解決問題的能力及探索合作精神，又能使學生深刻體會數學中局部與整體的辯證關系，從而使學習高等數學更有成就感.

二、教學過程研究

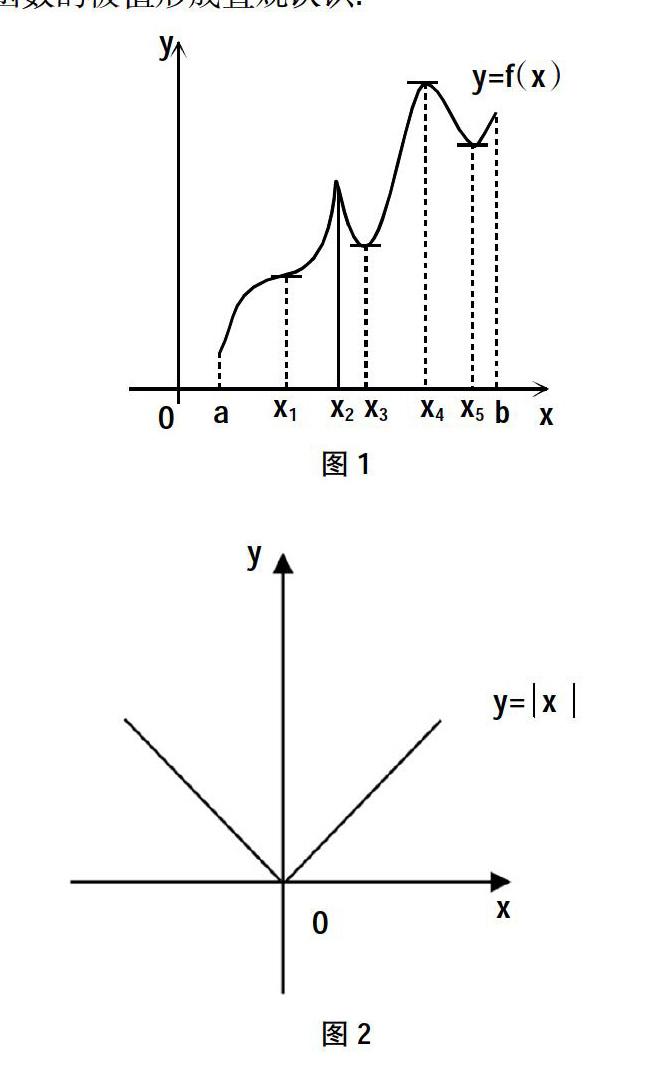
首先，教師借助多媒體展示山勢連綿起伏的圖片并提示學生觀察山峰和山谷的地勢特點.接下來展示以下圖形，并告知學生函數的極值研究的就是函數圖像的“山峰”和“山谷”問題，使學生對函數的極值形成直觀認識.

學生觀察圖1的函數圖像并思考：函數圖像在點x1，x2，x3，x4，x5處的函數值與其近旁的點的函數值對比有怎樣的大小關系.學生仔細比較觀察不難發現，f（x2）、f（x4）對應的函數值都比其近旁的函數值大，f（x3）、f（x5）對應的函數值都比其附近的函數值小.此時，教師引入函數極值的概念，即：

定義1：設函數在區間（a，b）內有定義，x0∈（a，b），如果對x0兩側近旁的任意點x（x≠x0），均有f（x）f（x0）成立，則稱f（x0）是函數f（x）的一個極小值，x0點稱為f（x）的極小值點.

分析理解極值定義，學生很容易判斷出f（x2）、f（x4）為極大值，f（x3）、f（x5）為極小值.接著教師引導學生總結得到：只要函數圖像出現“山峰”的形狀就可以出現極大值，出現“山谷”的形狀就可以出現極小值，并且得出函數的極值一定出現在區間內部，在區間端點處不能取到極值.隨即教師繼續提出問題：極大值是不是一定比極小值大？在一個區間上極值是否是唯一的？學生通過對比討論圖1中的點x2和x5的函數值便可得到答案是否定的，并且能體會到函數在一個區間上的極值可以有多個.接著教師引導學生回憶函數曲線在某點的切線知識，提出問題：函數在以上極值點處的切線斜率有什么特點？學生通過分組討論探究不難發現：函數在取得極值處的切線往往是水平的，即切線斜率為零.從而，教師引入駐點的定義.

定義2：使f'（x）=0的點稱為函數的駐點.

如圖1中的點x1、x3、x4和x5處均是駐點，但是并非所有的駐點均取到極值，如點x1.同時，教師引導學生觀察點x2可以發現：在有垂直切線的點處也可以取到極值.進一步，教師引入的圖像y=x（圖2），顯然，x=0是此函數的極小值點，但是在x=0處不可導.最后，學生可以總結出：對一個連續函數f（x），在極值點處切線是水平的、垂直的或者切線不存在的，即極值點必是駐點或不可導點，但是駐點和不可導點不一定是極值點.教師提問：函數的駐點和極值點到底有怎樣的必然關系呢？學生經過思考后便可以得到極值的必要條件：

定理1：設函數f（x）在點x0處可導且取得極值，則必有f'（x）=0.

以上定理可以簡述為：可導函數的極值點一定是駐點，但是駐點不一定是極值點，學生通過觀察函數y=x3的圖像可知：駐點并不是其極值點.那么，教師繼續發問：在沒有函數圖像的情況下，如何確定一個可能極值點是否為極值點呢？學生根據圖1，聯系函數的單調性便很容易理解極值的第一充分條件.

定理2：設函數f（x）在點x0的某個空心鄰域內可導.

（1）如果當x取x0左側鄰域的值時，恒有f'（x）>0;當x取x0右側鄰域的值時，恒有f'（x）<0，那么函數f（x）在點x0處取得極大值f（x0）.

（2）如果當x取x0左側鄰域的值時，恒有f'（x）<0;當x取x0右側鄰域的值時，恒有f'（x）>0，那么函數f（x）在點x0處取得極大值f（x0）.

（3）如果在x的兩側，函數的導數符號相同，那么函數f（x）在點x0處不取得極值.

接下來，教師采用下列例題與學生一起熟悉極值的判定過程.

教師引導學生書寫求解的過程，不僅復習了函數單調性的判斷方法，而且將極值的第一充分條件理論轉化為實踐，加深對定理的理解運用.此外，采用列表法求解清晰簡練，能使學生深刻體會數學的簡潔美.緊接著，教師指出函數極值的判斷除了可以用函數的一階導數f'（x）判斷外，還可以用函數的二階導數f''（x）來判斷.如果f（x）在駐點x0處的二階導數f''（x0）存在且不為零，則可用極值的第二充分條件判斷x0是極大值點還是極小值點.教師提示學生可根據圖1中極小值點x3和極大值點x4附近函數圖像切線的斜率變化即一階導數f'（x）的單調性來理解極值的第二充分條件.

定理3：設x0為f（x0）的駐點，即f'（x0）=0，但f''（x0）≠0，則

（1）當f''（x0）>0時，x0為極小值點;

（2）當f''（x0）<0時，x0為f（x）的極大值點.

值得注意的是，如果f'（x0）=0且f''（x0）=0，則x0點可能是也可能不是極值點，這時仍需用定理2來判定，所以定理3雖然判斷的過程比較簡單，但是相對于定理2而言應用有一定的局限性.對定理2的理解，教師可指導學生通過以下例題分組自行討論解決.

例2：求函數f（x）=2x3-6x2-18x-10的極值.

解：f（x）在（-∞，+∞）內均可導，且

f（x）=6x2-12x-18=6（x2-2x-3）=6（x-3）（x+1）

令f'（x）=0得駐點為：x1=1，x2=3

且f''（x）=12x-12，

由于f''（-1）=-24<0，故x=-1是函數的極大值點，極大值為f（-1）=0，

由于f''（3）=24>0，故x=3是函數的極小值點，極小值為f（3）=-64.

函數極值在實際生活中有著廣泛的應用.利用函數極值可以解決在一定條件下成本最少、利潤最大、原材料最省等問題，這些問題反映在數學上就是求函數的最值問題.函數的最大值和最小值統稱為最值.教師繼續引導學生觀察圖1并提問函數y=f（x）在區間[a，b]上的最大值和最小值出現在哪里？學生通過觀察很容易發現函數y=f（x）在區間[a，b]上的最大值和最小值分別在點x4和a處取到，其中，x=a是區間的左端點，x=x4是極大值點.接著教師指出最值和極值最明顯的區別：最值是整個區間上的所有函數值中最大和最小者，它是一個全面、整體性概念.再根據閉區間上連續函數的性質，閉區間上的連續函數最大值和最小值可以在閉區間的內部取到也可以在區間的兩個端點處取到，教師引導學生一起總結歸納出函數在區間[a，b]上求最值的步驟：（1）求出f（x）在區間[a，b]上的所有駐點和不可導點;（2）求出駐點、不可導點及區間端點所對應的函數值;（3）對以上函數值比較大小，其中最大的即為最大值，最小的即為最小值.此時教師可安排學生自己求解函數f（x）=x3-x2-2x+3在[2，6]上的最大值和最小值作為課堂練習.

最后，教師需要特別指出的是：函數f（x）在一個區間（有限或無限，開或閉）內可導且只有一個駐點x0，并且此駐點是f（x）的極值點，那么，當f（x0）是極大（小）值時，f（x0）就是f（x）在該區間上的最大（小）值.往往在實際問題中，由實際經驗可知，函數f（x）在定義的區間內部的確有最大值或者最小值，而此時只有唯一的一個駐點，就可以判斷f（x）在唯一駐點處取得相應的最大值或者最小值.但是，對此理論，有一部分高職學生理解不夠深入，教師可以跟學生一起探討如下例題.

例3：用鐵皮做成一個容積一定的圓柱形無蓋容器，忽略材料厚度的情況下，問應當如何設計，才能使得用料最省？

以上教學過程設計充分地體現了數形結合思想，通過簡單的圖形將眾多抽象的數學知識形象表現出來，使學生親身感受數學的應用價值，從心靈上感知數學來源于生活，又回歸到生活，激發數學學習的興趣，增強對數學學習的認同感.

參考文獻：

[1]王艷芬.關于高職數學函數連續性的教學過程研究[J].廣東教育，2019（2）：81-82.

[2]汪富泉，王艷芬.高等數學[M].長春：吉林大學出版社，2016.

[3]鄭桂梅.高等數學[M].長沙：國防科技大學出版社，2008.

[4]同濟大學應用數學系.高等數學（上冊）[M].第五版.北京：高等教育出版社，2002.

[5]侯風波.高等數學[M].上海：上海大學出版社，2009.

◎編輯 陳鮮艷