創造性思維的培養在幾何教學中的實踐與思考

韓穎 奚燕

一、問題的提出

創造性思維是以感知、記憶、思考、聯想、理解等能力為基礎，它的過程離不開繁多的推理、想象、聯想、直覺等思維活動。通過發展幾何直覺，進行合理的想象、聯想等，對具體教學內容進行綜合的分析推理，從而改善學生思維習慣，解決學生沒有思路、無從下手的苦惱。

教學實踐中，發現不少學生對于一些所學定理有先入為主的固定思維模式，再有其他優勝的方法也不易被其發現和利用，不利于創造性思維的培養。教師一開始就應破除這種模式，給學生提供一個能夠把問題發散的創新環境，廣闊深入地探究發現各種不同的方法， 從而進行創造性思維的培養。

二、實踐與思考

每講到角平分線的性質定理，學生做題時就先入為主，角平分線上的點到角兩邊的距離相等，但方法不一定簡單。直接給了基本模型再做題，效果也并不理想。

在我不斷學習總結國內外理論和實踐反思中，我把創造性思維在幾何教學中的培養分為三個層次：發展直覺，有效聯想，引導發散，并使三個層次之間密切配合。

1.操作觀察，發展直覺

所謂直覺思維，是指不經過一步一步分析而突如其來的領悟或理解。很多心理學家認為它是創造性思維活躍的一種表現，它既是發明創造的先導，也是百思不解之后突然獲得的碩果。

活動一：復習回顧，引入新知。

問題1：全等三角形的判定方法有哪些？

問題2：給你一個三角形，你能用折紙的方法確定其中一個內角的角平分線嗎？利用角平分線你能剪出一對全等的三角形嗎？

折剪紙的過程就是挖掘數學本質的過程，不僅直觀形象，還發展了幾何直覺。折紙出現的折痕就是三角形的角平分線，即公共邊，一個內角被平分成兩個相等的角，還有一組邊部分重合，為構造全等三角形提供了兩個條件。剪紙是為了讓一組邊或角相等，從而滿足全等三角形判定的3個條件。

幾何直覺在創造活動中有著非常積極的作用，一是能迅速作出優化選擇，二是能作出創造性的預見。

2.夯實基礎，有效聯想

聯想思維是一種把已經掌握的知識與某種思維對象聯系起來，從其相關性中發現啟發點，從而獲取創造性設想的思維形式。

活動二：聯想判定，探究構造。

問題3：如下圖，點P是∠AOB平分線OC上一點，請你利用角平分線添線，添加一個能直接判定三角形全等的條件，并在圖中用標記符號標記這個條件，寫出構造全等三角形的判定方法。（盡可能用多種判定方法構造）

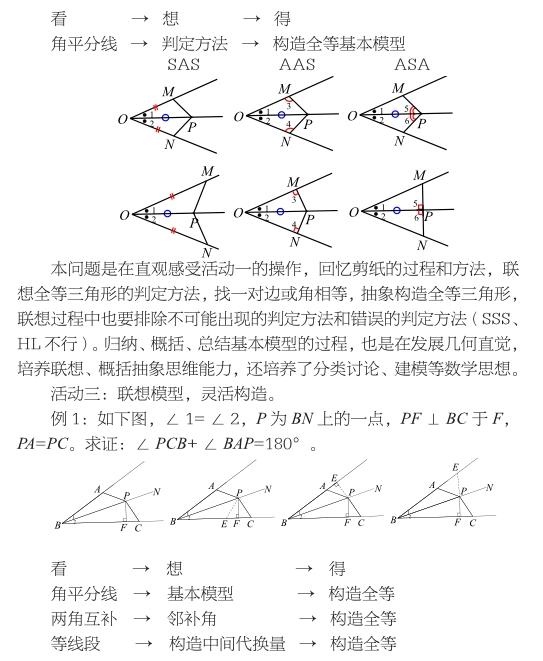
本題目對于剛學習添輔助線解決幾何問題的學生來說是非常困難的，學生對條件、結論、圖形都需要進行有關聯想，并排除無關定理。

設計中培養聯想思維的活動環環相扣，從建立模型到歸類簡化模型，再到模型的應用，層層遞進，無不體現出聯想的重要性。聯想思維的培養是創造性思維培養的先驅，是必經之路，是重要橋梁。

3.精心設計，引導發散

心理學家吉爾福特認為，創造性思維的核心就是發散思維。上述活動中，剪紙的不同剪法呈現出不同的三角形的形狀；畫圖構造全等三角形，利用不同的判定方法構造不同模型；在解例1的過程中用不同的解法，學生能從已知、求證、圖形特征等不同角度出發提出、分析、解決問題；在一題多解的基礎之上進行方法擇優，從求證出發的逆向解題思維，從圖形特征發展直覺的解題思維都給學生留下了深刻的印象，改編題目等等，都是在更好地進行發散思維的培養。

三、反思總結

創造性思維的培養單靠教材是完不成的，因教材要盡量適合所有學生，有一定的局限性，所以首先應鼓勵和激發教師創造性地使用教材，以彌補教材的不足。由學生自己提出問題、分析問題、解決問題才是終結完成一系列創造性思維的過程。

在教師引導、啟發學生經歷“直覺——聯想——發散”等精心設計的教學環節并進行綜合整合分析的實踐過程中，我和學生互相啟發學習，學生由被動學習變成了主動研究，把“學幾何”變為“玩幾何”，改善了學生的思維習慣，解決學生沒有思路、無從下手的苦惱，脫離死記硬背的解題思路，跳離了題海戰術，親身體驗、主動創造給他們帶來了驚喜與快樂，真正達到了研究性創新學習的目的。

【參考文獻】

[1]陳龍安.創造性思維與教學[M].北京：中國輕工業出版社，2000.

[2]孫延洲.基于創新思維培養的中學數學教育研究[D].華中師范大學，2012.

【備注：本文為北京市教育科學“十二·五”規劃2015年青年專項課題《在初中圖形與幾何課堂教學中培養學生數學創造性思維的對策研究》（課題批準號：CBA15053）的研究成果】