高速鐵路軌道的波阻抗及影響因素研究
曹曉斌,唐逢光,何 飛,何祥照,傅 祺
(1.西南交通大學電氣工程學院,成都 610031; 2.中國鐵路成都局集團供電處,成都 610081)
1 概述
高速鐵路的軌道不僅是引導列車前進的導行軌,還是牽引電流的重要回流路徑,同時是信號系統中重要的一環[1]。近些年來,我國高鐵快速發展,軌道暫態過電壓問題也逐漸增多。軌道暫態沖擊過電壓主要發生在雷擊、接地短路的瞬間,以及列車經過絕緣節等暫態過程[2-3],暫態過電壓的幅值由沖擊電流和軌道的波阻抗共同決定,因此計算軌道的沖擊過電壓水平,必需首先計算出軌道的波阻抗。
國內外很多學者開展了高鐵軌道電氣參數的研究,如文獻[4-5]研究了高鐵軌道的工頻阻抗;文獻[6-9]通過建立軌道的分布參數模型,研究了軌道電位及降低軌道電位的措施;文獻[10]通過在秦沈客運專線軌道阻抗參數實測,分析了無砟軌道對軌道電路的影響。文獻[11-13]在EMTP中采用CP模型加漏泄電阻的方法,對軌道電氣模型進行了改進。文獻[14-16]根據軌道交通線路阻抗和導納理論,求出了工頻下軌道的自阻抗與互阻抗。
上述文獻研究了軌道的工頻阻抗,但高鐵軌道是具有分布參數的電路元件,在高鐵站場發生雷擊等沖擊電路的作用下,會產生沿線路方向傳播的沖擊過電壓[17-18]。本文對軌道模型進行精細劃分[19-20],通過分析直角沖擊波在軌道中的傳播規律,對高鐵軌道的波阻抗與影響因素開展研究。
2 軌道的仿真模型及原理
2.1 軌道的仿真模型
考慮到電壓波會在復線上下行鋼軌橫向連接線處產生復雜的折反射過程,不能用單一波阻抗表示,而對于高速鐵路復線軌道,在其每個股道末端均可以用單線軌道波阻抗等效處理。因此,重點研究單線軌道波阻抗建模計算方法。根據文獻[3]中高速鐵路軌道的結構與參數,利用EMTP仿真軟件,以經典貝杰龍模型為基礎,建立了高鐵軌道的仿真模型,如圖1所示。
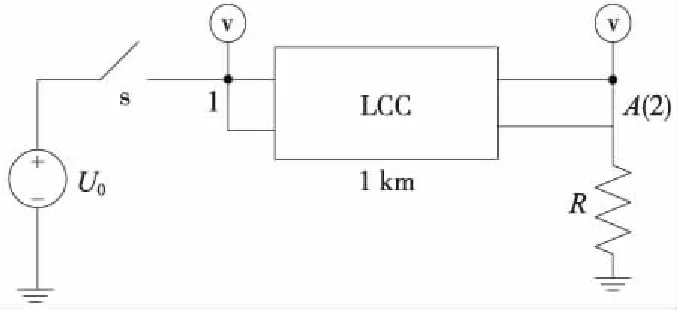
圖1 高速鐵路軌道仿真模型
模型中軌道選用P60型鋼軌,其中鋼軌等效半徑設置為1.285 cm,電阻為0.135 Ω·km-1,兩根鋼軌之間的距離設置為標準的1.435 m。水平高度設置為0.2 m,土壤電阻率為100 Ω·m,在線路首端用一個直流電壓源作為激勵源,其幅值為100 V,線路末端與大地之間串入1個電阻作為末端電阻。
首先,考慮只有一段1 km長的軌道時,軌道的漏泄電阻與末端電阻合并,即線路1為1 km長的軌道,根據電阻的波阻抗特性,電阻R相當于波阻抗為R的無限長線路,下文中可以用線路2替代。設置2個電壓觀測點:1點為入射點電壓觀測點,2點(即A點)不僅是末端電阻電壓觀測點,也是線路1與線路2串聯點的電壓觀測點。
2.2 直角波在模型中的傳播
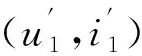
線路1的波阻抗即為軌道的波阻抗,設為Z1,另一條線路的波阻抗為Z2,在圖1的模型中,Z2=R。
3 軌道的波阻抗研究
3.1 軌道波阻抗的計算原理
以圖2為例,當線路2為無限長時,節點A滿足以下邊界條件。
線路1的總電壓和電流為
(1)
線路2的總電壓和總電流為
(2)
根據邊界條件,在節點A處只能有1個電壓,即
(3)
因此可得
(4)
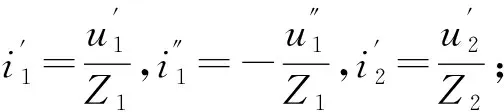
(5)
式中α——電壓折射系數;
β——電壓反射系數。
根據上述結果可以得出:
(1)當Z2=Z1時,α=1,β=0;這表明電壓折射波等于入射波,而電壓反射波為零,即不發生任何折、反射現象;
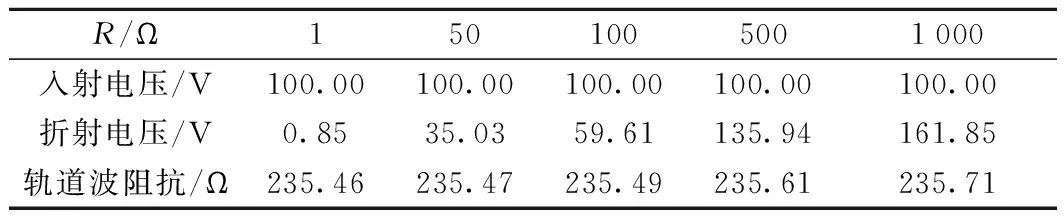
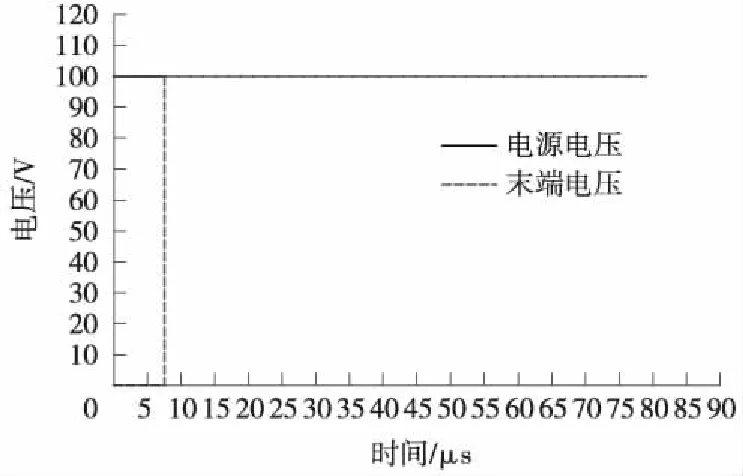
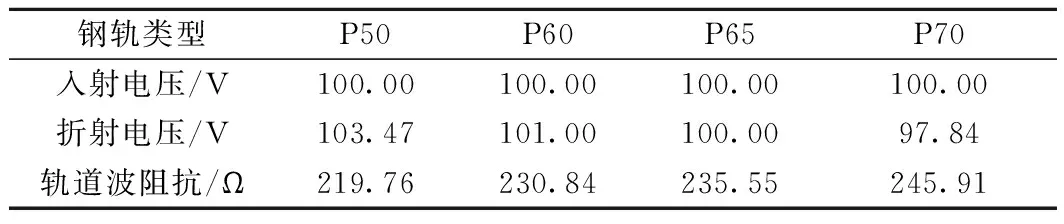
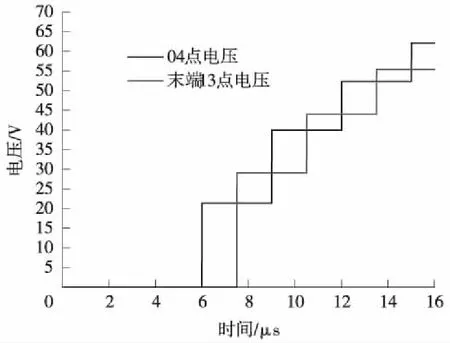
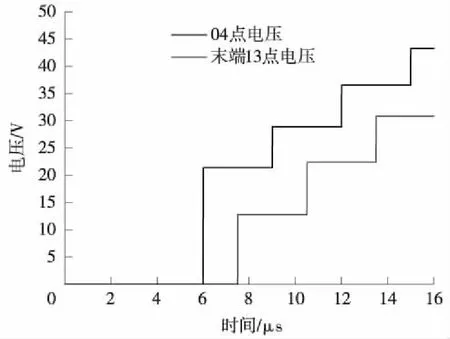
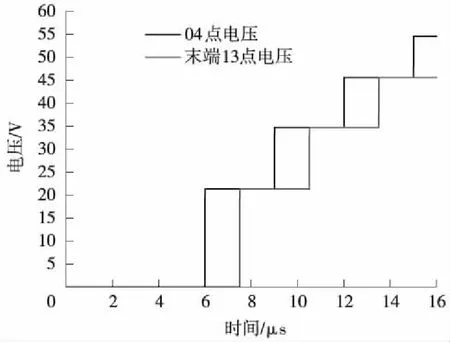
(2)當Z2 (3)而當Z2>Z1,α>1,β>0;而電壓反射波與入射波同相,疊加后使線路1上的總電壓大于電壓入射波,使線路1上的總電壓增高,即A點發生正反射現象。 (6) 由式(6)變形可知 (7) 即在線路末端設置一個電阻值為R的電阻,在首端施加一個U0的直流電壓,可根據A點響應電壓u2第一次響應幅值,計算得到線路的波阻抗,如果發生了多次折反射,則式(7)不再適用。因此,計算過程中必需找出第一次折反射發生的時間與電壓幅值。 考慮到輸電線路的波阻抗在300 Ω左右,驗證時從100~500 Ω的阻值來模擬軌道的末端電阻,分兩種情況進行對比分析。 (1)末端電阻較大 電源電壓取100 V,R取值500 Ω,得到電壓波形如圖3所示。從圖3中可以看出,末端的第一個電壓波大于入射電壓,即t0時刻在A點發生了反射現象,由于A點反射電壓在線路端點1與2之間反復傳播,因此末端電壓以電源電壓為基準,呈現振蕩衰減的波形。 圖3 末端電阻大于軌道阻抗時的波形 (2)末端電阻較小 電源電壓取100 V,R取值100 Ω,得到電壓波形如圖4所示。從圖4可以看出,末端的第一個電壓波小于入射電壓,即t0時刻在A點發生了折射現象。節點A處發生的折反射電壓波同樣在線路中反復傳播,因此末端電壓以電源電壓為基準,呈現階梯狀上升波形。 圖4 末端電阻小于軌道波阻抗時的波形 根據波過程理論,當末端電阻與軌道波阻抗不相等時,波形會出現波動和攀升,主要是因為電壓波會在軌道上不停地發生折反射過程, 以第二段線路上的末端電壓為例,在第一種情況中,電壓波首次到達末端時,發生一次折反射,折射電壓為αU0,反射電壓為βU0,反射電壓經過軌道回到電源端時,再反射到末端時電壓反向,此時再發生一次折射,折射電壓為-αβU0,故總的折射電壓為αU0-αβU0,由于β是正數,所以電壓在第二段線路會降低。而到第三次折射時,第二次的折射電壓又會反向,故在此種情況下,末端電壓會成上下波動狀,以此類推,直至末端電壓接近電源電壓。可以推出末端電壓公式為 Ut=αU0-αβU0+…+(-1)n+1αβn-1U0 (8) 式中,Ut為末端電壓;n為反射波到達節點A的次數;α為折射系數;β為反射系數;U0為電源電壓。 在電壓波到達軌道末端的t0時刻之前,末端電壓一直為零,而在t0時刻,電壓波到達末端A點,發生折、反射。此時的末端電壓值u2就是折射電壓值。由仿真數據可知,在上述各圖形中,電壓波到達末端的時間均是t0=7.53 μs,而軌道的長度是固定的,為1 km,故可求出軌道中的波速ν=1.328×108m/s,而每一段線路電壓穩定的時間則是τ=15.06 μs。 所以在圖3中反射電壓為末端電壓在t0時刻的值,由仿真數據可知即為135.93 V,入射電壓由于被直流電壓強制為100 V不變,故根據公式(7)可解得Z=235.551 Ω。 當末端電阻較小時,即在第二種情況中,第二段線路時間上的折射電壓依然為αU0-αβU0,不同的是此時β是負數,所以電壓在第二段線路會升高,而且會一直升高,直至接近電源電壓,但升高的幅值會越來越低。 因此,在圖4中折射電壓為末端電壓在t0時刻的值,由仿真數據可知即為59.61 V,入射電壓由于被直流電壓強制為100 V不變,故根據公式(7)可解得Z=235.49 Ω。 根據上述計算結果,取二者的平均值,仿真模型中軌道的波阻抗為235.52 Ω。 目前尚無軌道波阻抗的計算方法相關研究報道,無法做計算波阻抗值的對比分析,因此本文根據波阻抗的定義以及式(8),可以推斷軌道的波阻抗的幾個固有特點: (1)軌道的波阻抗與末端阻抗的取值無關,無論其末端阻抗取值為多少,通過式(7)計算得到的結果基本相同; (2)通過式(5)、式(6)與式(8)可知,α=1,β=0,即當末端阻抗與軌道波阻抗相同時,末端電壓將沒有圖3與圖4的類似過渡過程。 (3)無論軌道模型的分段數量以及分段長度如何改變,其計算得到波阻抗不變。 為了檢驗本文研究的方法正確性和精度,將從上述3個方面進行檢驗。 為了驗證第3節計算的結果,從1~1 000 Ω選取5個不同的阻值進行仿真計算,入射電壓均為電源電壓100 V,利用公式(7)計算結果如表1所示。 表1 不同末端電阻時軌道波阻抗 根據這5組軌道波阻抗數據,取其平均值為235.55 Ω,最大誤差為0.06%。因此,可以證明利用本文提供的方法,計算結果不受末端阻抗取值的影響,滿足波阻抗的第一個特性。 將軌道波阻抗值取為235.55 Ω,并代入圖1的仿真模型,得到A點的電壓響應波形如圖5所示。 圖5 末端電阻等于軌道阻抗時的波形 從圖5可知,此時末端電壓與入射電壓基本一致,此時既沒有發生折射也沒有發生反射,α=1,β=0,末端電壓滿足公式(8),驗證了軌道波阻抗的值就是235.55 Ω。同時也證明在軌道末端串接1個阻值為235.55 Ω的電阻時,末端電壓與無限長軌道的情況相同。 考慮到電壓波在軌道中的傳播會受到土壤電阻率的影響,因此從10~1 000 Ω·m選取5個不同的阻值進行仿真計算,入射電壓均為電源電壓100 V,利用公式(7)計算結果如表2所示。 表2 不同土壤電阻率時軌道波阻抗 從表2可以看出,軌道波阻抗會隨著土壤電阻率的增大而增大。本文結論即P60型軌道波阻抗為235.55 Ω,是基于土壤電阻率為100 Ω·m時提出的。 高速鐵路軌道一般常用的鋼軌類型有P50、P60、P65、P70等幾種,這幾種不同類型的鋼軌主要是鋼軌等效電阻及等效半徑不相同,仿真結果如表3所示。 表3 不同鋼軌類型時軌道波阻抗 從表3可以看出,不同類型的鋼軌會有不同的軌道波阻抗,而且軌道波阻抗會隨著單位長度鋼軌的增大而略微增大。主要原因是各種類型的鋼軌截面相差不是很大,所以其等效電阻和等效半徑相差不大。 通過上述仿真結果可以發現,高速鐵路軌道的波阻抗在210~250 Ω變化,均小于架空輸電線路的300 Ω標準。 由于軌道與大地之間存有過渡電阻,理論上可以將一段軌道分成無數段,本節將1 km軌道分成五段LCC模型,LCC模塊參數同上,不同的是每一段都有接地電阻模擬軌道對地的漏泄電阻,其值為100 Ω·km,然后按照實際長度作變換。例如0.2 km時,則漏泄電阻設為500 Ω·km。末端電阻設為100 Ω。五段LCC模型時的軌道模型見圖6。其各節點電壓和末端電壓的關系見圖7。 圖6 五段LCC模型時的軌道模型 圖7 各節點電壓波形 根據電壓波到達的時間不同,上述波形依次是05、07、09、04、13點電壓各點的波形。經仿真計算,利用彼得遜法則,將每一節點上的軌道漏泄阻抗與相鄰LCC等效成集中參數的電阻,計算可知每一部分的LCC模型均可用等效電阻R來計算,R0是軌道漏泄電阻。 圖8就是利用彼得遜法則建立的一段LCC等效電路,其中U0是LCC前面一個點的電壓,例如要求05點的電壓,則U0就是03點的電壓,以此類推,每一段的LCC模型都等效成電阻R,這樣根據仿真結果可以計算得出R=470.8 Ω。代入電路中即可得每一段LCC上的首段電壓均可用式(9)算出 圖8 簡化電路模型 (9) 式中,Un為第n段LCC上的首段電壓;m為每千米軌道分成m段;U0為電源電壓。 由于軌道被分成五段LCC模型,故此時末端的入射電壓為04點的電壓。末端電阻的數值與一段LCC模型時取值一樣,分3種情況進行仿真計算。 (1)當末端電阻大于軌道波阻抗時,折射電壓大于入射電壓,末端電阻R取值500 Ω,波形如圖9所示。 圖9 末端電阻大于軌道波阻抗時的波形 從圖9的波形可知,04點電壓與線路末端(13點)的電壓波形不同,即末端對04點的電壓存在折反射的影響。 04點第一個波形的電壓為21.366 V,而末端電壓根據仿真結果可知為29.055 V。將上述參數代入公式(7)可得Z=235.36 Ω。 (2)當末端電阻小于軌道波阻抗時,折射電壓小于入射電壓,末端電阻R取值100 Ω,波形見圖10。 圖10 末端電阻小于軌道波阻抗時的波形 04點電壓與末端電阻值無關,依然為21.366 V,而末端電壓根據仿真結果可知為12.742 V。將上述參數代入公式(7)同樣可得Z=235.36 Ω。 從1~1 000 Ω選取5個不同的阻值進行仿真計算,入射電壓均為04點電壓,折射電壓為13點t0時刻的電壓,利用公式(7)計算結果見表4。 表4 五段LCC模型時不同末端電阻時軌道波阻抗 根據這5組軌道波阻抗數據,取其平均值為235.38 Ω,與一段LCC模型時的軌道波阻抗值235.55 Ω誤差為0.07%。故仍然可以判定軌道波阻抗數值為233.5 Ω,即不論軌道是否存在對地泄漏電阻,采用第4節方法均可計算得到軌道波阻抗的模值,且該模值與軌道是否存在對地泄漏電阻無關。 (3)當末端電阻等于軌道波阻抗時,電壓波形不發生折反射,末端電阻R取值235.55 Ω,波形見圖11。 圖11 末端電阻等于軌道波阻抗時的波形 此時末端電壓與04點的電壓波形完全一致,只是有一個由于兩點之間的距離產生的時間差。說明電壓波在末端沒有發生折、反射,與末端接無限長的軌道一致,滿足波阻抗的特性,因此驗證了本文對于軌道波阻抗的計算方法是準確的。 本文研究了高速鐵路軌道的波阻抗及影響因素,主要結論如下。 (1)根據波阻抗的理論,提出利用仿真得到的末端電阻上電壓的波形計算軌道波阻抗的方法;并給出了波阻抗的計算公式,以P60型軌道為算例,演示了波阻抗的計算過程,得到該型軌道數值為235.55 Ω,并利用波阻抗的物理特性對該結果進行了驗證。 (2)研究了土壤電阻率、鋼軌類型對軌道波阻抗的影響,土壤電阻率與鋼軌類型對軌道的波阻抗均有較大的影響,土壤電阻率越大,波阻抗越大;鋼軌的等效半徑越大,波阻抗也越大。其波阻抗值在210~250 Ω變化,均小于架空輸電線路的波阻抗。 (3)軌地過渡電阻對軌道波阻抗沒有明顯的影響,因此在軌道建模中,末端阻抗按線路波阻抗取值,不需要考慮鋼軌對地過渡電阻的影響。由于軌道波阻抗由鋼軌固有參數決定,該計算方法不僅適用于高速鐵路還適用于普速鐵路。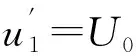
3.2 軌道波阻抗末端電壓仿真結果
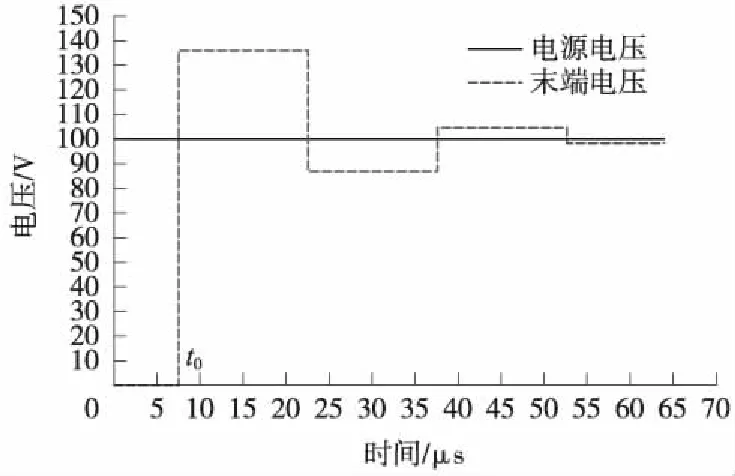

3.3 軌道波阻抗計算結果分析
4 軌道波阻抗驗證
4.1 驗證原理
4.2 不同末阻抗對軌道波阻抗計算結果的影響
4.3 末端阻抗等于軌道波阻抗時的過渡過程分析
5 軌道波阻抗的影響因素研究
5.1 土壤電阻率對波阻抗的影響
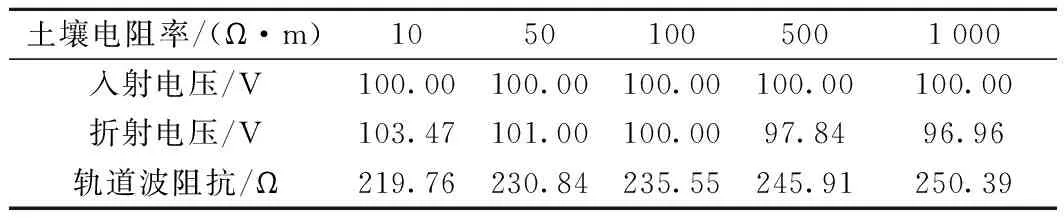
5.2 鋼軌類型對波阻抗的影響
6 過渡電阻對軌道波阻抗的影響研究
6.1 有損軌道模型介紹
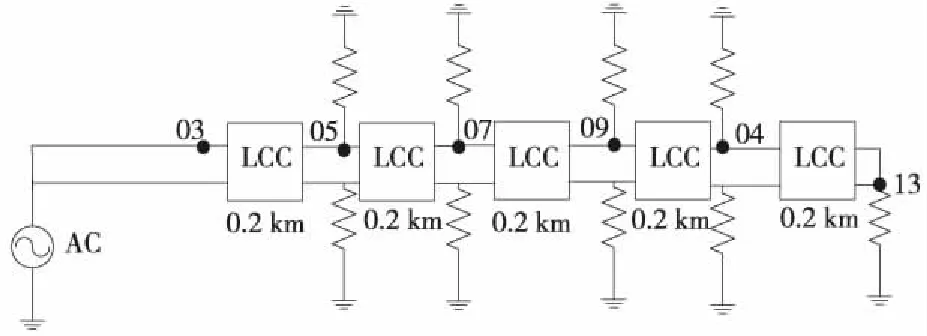


6.2 五段LCC模型時的不同末端電阻對仿真結果的影響

7 結論

