到定點與定直線的距離差為定值的點的軌跡的探究
商軼瑋
(上海市北虹高級中學 200080)
一、提出問題
例題(滬教版高二下第12.7節) 動點P(x,y)到定點F(2,0)的距離比它到定直線x+4=0距離小2,求動點P(x,y)的軌跡方程.
變式動點P(x,y)到定點F(2,0)的距離比它到y軸的距離大2,求動點P(x,y)的軌跡方程.

反思經歷了上述的錯誤,很多同學再遇到類似的問題時,難免困惑——到定點與定直線的距離的差為定值的動點的軌跡到底是什么?何時才是一條拋物線?
二、探究過程
我們可以從“數”與“形”兩個角度來進行分析.
1.幾何方法:不妨設動點P到定點F的距離為d1,到定直線l的距離為d2,定點F到定直線l的距離為d.
當d1=d2時,由拋物線定義可知,點P的軌跡是一條拋物線(F?l);或是一條過點F且垂直于l的直線(F∈l).
當d1
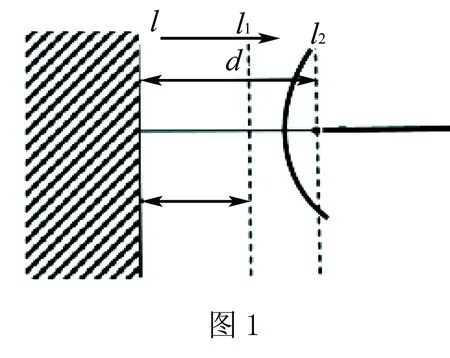
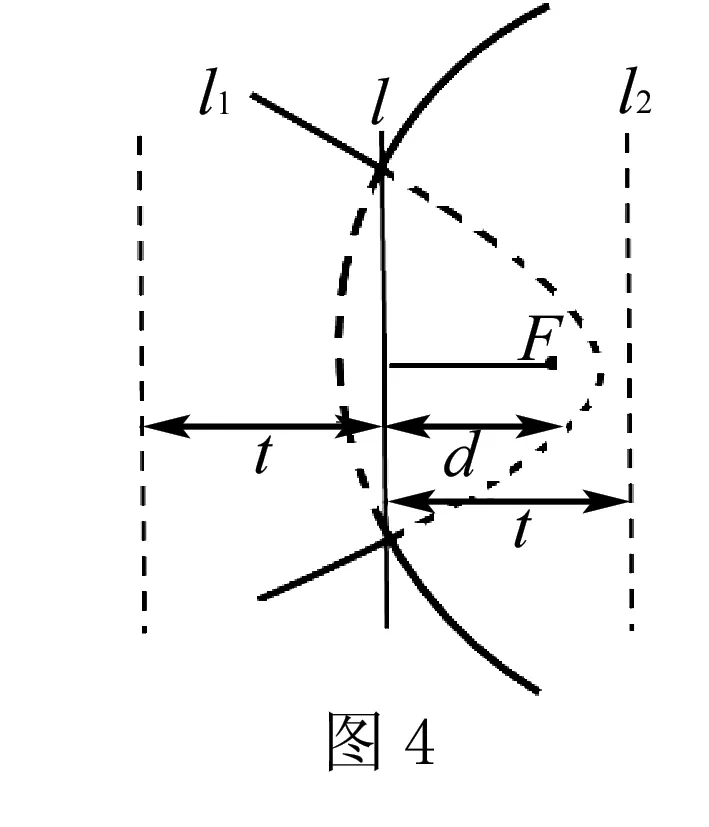
(1)若t (2)若t=d,如圖1,可將直線l向右平移t個單位至直線l2,即動點P到點F和直線l2的距離相等,所以動點P的軌跡就是以為定點F為端點一條垂直于l2的射線(方向向右) (3)若t>d2,若將直線l向右平移t個單位,則“越過”了定點F,顯然不成立,故動點P的軌跡不存在. 當d1>d2時,令d1-d2=t(t>0). (1)若t (2)若t=d,如圖3,此時動點P的軌跡既可以出現在直線l的右側,又可以出現在直線l的左側.直線l右側的軌跡可將直線l向左平移t個單位至直線l1,所以在直線l的右側動點P的軌跡就是以點F為焦點,以l1為準線的一條拋物線(頂點為O).顯然,直線l左側的軌跡是一條以O為端點的向左的射線.綜上所述,動點P的軌跡是一條拋物線加上一條射線. (3)若t>d,如圖4,此時動點P的軌跡既可以出現在直線l的右側,又可以出現在直線l的左側.對于直線l右側的軌跡,可以將直線l向左平移t個單位至直線l1,所以動點P的軌跡就是以點F為焦點,以l1為準線的拋物線在直線l右邊的部分;同樣對于直線l左側的軌跡,可以將直線l向右平移t個單位至直線l2,所以動點P的軌跡就是以點F為焦點,以l2為準線的拋物線在直線l左邊的部分. 綜上所述,動點P的軌跡是兩條拋物線各取一部分. 兩邊平方并化簡得,y2=t2-d2+2dx+2t|x|,即y2= 1.通過以上探究過程,不難發現,平面內到定點與定直線的距離的差為定值的動點的軌跡大致分為三類八種情況. 2.可以歸納出,定值t當且僅當-d 3.拋物線定義的推論:平面內到定點F與定直線l(F?l,F到l的距離為d)的距離的差為常數t(|t|
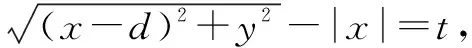



三、一般結論

