物流業發展的區位差異、驅動因素及時空異質性研究
——基于GTWR模型的分析

唐建榮 張鑫和 類延波

(江南大學 商學院，江蘇 無錫 214122)

一、引言及文獻綜述

中國物流與采購聯合會公布的《2016年全國物流運行情況通報》指出，2016年中國社會物流總額達229.7萬億元，按可比價格計算比上年增長6.1%，增速提高了0.3個百分點。由此可見，隨著社會經濟的穩步增長，物流服務需求也隨之水漲船高。事實上，中國物流業在快速發展的同時也存在諸多問題，如“東強西弱”的集聚態勢、兩極分化的“馬太效應”等(唐建榮 等，2017)。在此背景下，剖析物流產業的發展演化規律及其差異成因成為學術界關注的熱點。

近年來，對物流產業發展驅動因素的相關研究屢見不鮮。如王健等(2014)采用向量自回歸模型、格蘭杰因果檢驗等方法對影響區域物流發展的因素進行的動態分析；唐建榮等(2015)基于經濟、支撐和信息視角，運用結構方程模型，分析了城市物流業發展的驅動因素，同時對比了各區域的發展差異；陳恒等(2015)利用LMDI指數法分析了勞動力投入對于物流業發展的驅動效應，并甄別了影響物流業發展的要素；謝守紅等(2015)利用TOPSIS法測算了長三角地區16市的物流業發展水平，結合嶺回歸方法探討了城市物流業發展的驅動因素。這些研究從不同角度探討了物流產業發展的驅動因素，但均未將產業發展的空間異質性納入研究視域，從而忽略了地理單元之間的聯系，導致分析結果可能存在偏差情況。

隨著空間計量方法的發展，包含空間滯后和空間誤差等在內的常系數模型被廣泛應用于克服產業發展的空間自相關性，如蔡海亞等(2016)采用空間計量模型(SEM模型和SAR模型)分析了長江三角洲物流產業發展的時空格局演變及影響機理。然而，物流產業發展是經濟水平、基礎建設、資源稟賦等多核共振的結果，作用機理復雜，且不同時空分布下各驅動因素的作用力大小和方向并不盡相同。若要兼顧不同的作用，并識別區域特質因素的影響強度，此時常系數空間計量模型便不再滿足研究要求。

20世紀90年代中期，地理加權回歸模型(Geographical Weighted Regression，簡記為GWR)作為一種可識別空間非平穩性的局部變系數模型被提出并得到廣泛應用(Fotheringham et al.,1996)。GWR模型可以克服地理單元間的空間異質性，突破常系數模型的局限性，針對不同地區得出差異化的研究結論，其理論意義以及異質化的政策價值較為顯著，且具有“因地制宜”的效果(呂光樺 等，2011)，進而被廣泛應用于不同行業研究中(王愛 等，2017;馬勇 等，2017;Diniz-Filho et al.,2016;向書堅 等，2016)。但GWR模型只能對截面數據進行回歸，Wu et al.(2014)在GWR模型中加入時間效應，構建出時空地理加權回歸模型(Geographical and Temporally Weighted Regression，簡記為GTWR)，可以在時間和空間兩個維度上捕捉不同空間單元的參數變異情況，從而可以有效彌補GWR模型的不足。時空地理加權回歸作為一種能夠有效識別非平穩性的方法，在理論上得到較好的發展，現實中也被廣泛的應用(Fotheringham et al.,2015;Guo et al.,2017;Chu et al.,2015;Liu et al.,2017;Bai et al.,2016)。

綜上所述，考慮時間因素的時空變系數模型對于面板數據的適用性大大增強，并具備更加優良的統計性質(韓兆洲 等,2017)，且目前國內外并不存在采用局部變系數模型研究相關問題的文獻。有鑒于此，本文利用2005—2015年中國31個省區的面板數據，從時空異質性的角度研究物流產業發展的驅動路徑，甄別出區域產業發展的“要核”，以厘清各因素間環環相扣的機制，進而準確揭示區域物流發展差異的癥結所在。與現有文獻相比，本文可能的貢獻在于：(1)研究視角上，從異質性角度出發，分析了物流產業驅動因素的空間差異及時序波動；(2)研究方法上，采用前沿的時空地理加權回歸模型，彌補了相關研究的空白，有效擴展了該方法的應用領域，豐富了物流產業發展的理論。

二、研究方法

為研究物流業的發展演化、驅動因素及其時空異質性，先利用TOPSIS模型評價物流產業發展水平，接下來利用核密度及探索性空間數據分析方法研究物流產業的演化狀況，最后構建GTWR模型分析物流產業發展的驅動因素及其時空異質性。

(一)TOPSIS模型

TOPSIS模型最早是由Hwang et al.(1981)提出的，這一方法核心思路是構造一組理想解，通過衡量所有決策方案的結果與理想解的逼近程度來比較不同方案的優劣，本文主要借鑒TOPSIS模型來構建評價各省區物流產業發展的綜合指標。熵權TOPSIS法是對傳統TOPSIS法的改進，即通過熵權法確定評價指標權重，再通過TOPSIS法利用逼近理想解的技術確定評價對象的排序(李沙浪 等,2014)。由于TOPSIS評價值是各省區的指標與正理想解和負理想解的相對余力，某個省區的評價值越高則該省區的各項指標離正理想解越近，這表示其物流產業發展水平越高。

(二)探索性空間數據分析

探索性空間數據法(ESDA)常用于分析空間數據自相關特性。空間自相關是指某要素與其鄰近要素屬性值在不同空間單元上的顯著程度，用于度量對象的空間集聚度和關聯性。本文通過全局Moran指數判斷物流業發展的空間相關性(李沙浪 等,2014)。全局Moran指數可以反映區域物流業發展空間分布特征，有效衡量空間鄰接的省區物流業發展水平的相似度，具體公式如下：

(1)

(三)核密度估計

核密度估計(Kernel)是一種非參數方法，可以將隨機變量的分布形態以連續的密度曲線形式予以反映，進而對變量的概率密度進行估計(Silverman,1986)。這一方法假定隨機變量x的密度函數為f(x)，在點x的概率密度可以用式(2)進行估計：

(2)

式(2)中：N為觀測值的個數；Xi為獨立同分布的觀察值；h為帶寬；x為均值；K(·)為核函數，核函數包括高斯核函數、Epanechnikov核函數等形式。本文采用高斯核函數進行估計，其表達式為：

(3)

核密度估計沒有確定的表達式，往往通過圖形分布的變化進行比較分析，而圖形中曲線可以反映變量的分布位置、形態和延展性等信息。

(四)地理加權回歸模型(GWR)

地理加權回歸模型(GWR)作為一種變系數空間回歸模型，常用于分析空間數據。地理加權回歸模型是運用局部多項式光滑技術對區域及其鄰近區域的觀測值進行全局最小二乘估計，進而得到每個地理區域對應的局部估計值，從而有效檢測出空間非平穩性(韓兆洲 等,2017)。

地理加權回歸模型的一般公式如下：

(4)

其中，ui、νi表示i地區的經度和緯度，即其具體的地理位置； βp(ui,νi)表示P個解釋變量的系數，且該系數是經緯度的函數；yi、xip分別表示被解釋變量、解釋變量；β0(ui,νi)為P個解釋變量的截距項；εi～iidN(0,σ2)表示模型的擾動項，反映的是空間隨機效應水平。

式(4)可用矩陣形式表示：

Y=(X?βT)I+ε

(5)

式(5)中：?表示矩陣的克羅內克積；I為(P+1)×1維的矩陣；X和βT為N×(P+1)維矩陣。

Brunsdon et al.(1999)利用加權最小二乘估計模型進行了修正：

(6)

式(6)中:矩陣W={wij}表示空間權重矩陣；Wij為區域i和區域j之間距離的衰減函數；βi=(βi0,βi1,…，βip)T(其中i=1,2,…,N)，表示第i個區域P個解釋變量組成的P維向量。

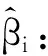
(7)

(8)

(9)

式(9)中：H=Xi(XTWiX)-1XTWi為帽子矩陣；Xi表示矩陣X第i行元素組成的P維向量。

進而求出模型殘差項γ及殘差平方和：

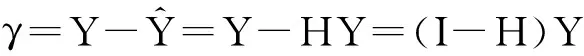
(10)

(11)

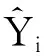
(12)

(13)

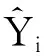
(14)

(15)

進而可求得殘差平方和為：

(16)

等式兩邊同時取期望可得：

E(γTγ) =E(tr(εT(1-H)T(I-H)ε))=tr(E(εT(I-H)T(I-H)ε))=tr(E(εTε)(I-H)T(I-H))=σ2(N+tr(HTH)-2tr(H))

(17)

化簡可得σ2的無偏估計：

(18)

σ2的估計值為：

(19)

式(19)中，2tr(H)-tr(HTH)為解釋變量個數，N-(2tr(H)-tr(HTH))為地理加權回歸模型的自由度。

(五)時空地理加權回歸模型

考慮到地理加權回歸模型忽略了時間效應的影響，進而導致參數估計的非平穩性。因此，可以進一步構建時空地理加權回歸模型(GTWR)作為分析工具：

(20)

式(20)中：yi為n×1維解釋變量；β0為常數項系數；(ui,vi,ti)表示第i個觀測點的經緯度坐標ui、vi[注]本文采用Gauss-Kruger Projection方法將觀測點橢球體坐標系下的經緯度轉為直角坐標系下的坐標。和觀測時點；βk(ui,vi,ti)為第k個因素在(ui,vi,ti)處的未知參數；xik是n×k維解釋變量；參數通過局部加權最小二乘法估計得出，即對于給定的一個觀測點，靠近該點的觀測值賦予較大的權重值，遠離該點的觀測值賦予較小的權重值，通過使得觀測值與擬合值差的加權平方和最小，從而可以求得參數的估計值。

GTWR模型的核心是空間權重矩陣的設定，時空權重矩陣一般構建為：W(ui,vi,ti)=diag(wi1,wi2,…,win)，其中對角線元素Wij是時空距離衰減函數。常用的權函數有距離閾值函數、距離反比函數、高斯函數和截尾型函數，這些函數共同特點是通過樣本點距離和效應隨距離的衰減程度來反映權重大小(Fotheringham et al.,1996)。本文采用高斯函數作為權函數，具體見式(21)：

(21)

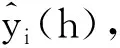
(22)

式(21)中，dij為i與j之間的時空距離，時空距離的測算涉及時間、空間雙維度，需要設定空間尺度參數λ和時間尺度參數μ，以此來平衡不同量綱間的差異。將給定的空間距離dS和時間距離dT綜合成時空距離dST，進而構建時空距離函數：

(23)

式(23)中，當λ=0時，表示不存在空間效應，時空距離為時間距離的比例函數，此時模型設定為TWR模型；當μ=0時，表示不存在時間效應，模型設定為GWR模型；當λ≠0且μ≠0時，則為GTWR模型。

由此，可以構建的時空權重矩陣表示為：(ui,vi,ti)=diag(wi1,wi2,…,win)，其中Wij的具體計算公式如下所示：

(24)

GTWR模型對每一個觀測的空間單元都進行了局部回歸，在地理位置的變化過程中對不同時點的每個參數進行估計，這能夠較好地反映各驅動要素的空間依賴性和時空差異性。

三、物流業發展水平測度及時空演化分析

準確評價各省區物流業發展水平是分析其演化狀況的基礎，有利于厘清物流業發展驅動機制的來龍去脈。本文利用2005—2015年中國31個省區面板數據，結合基于熵權的TOPSIS模型評價中國各省區物流業的發展水平，并利用核密度和探索性數據分析方法研究物流產業的時空演化狀況。

(一)指標體系構建與數據來源

通過對已有文獻的梳理發現，由于不同研究者研究視角和目標不同，其所構建的物流發展水平評價指標體系也不盡相同。本文在參考唐建榮等(2017)、謝守紅等(2015)研究的基礎上，構建出評價中國省區物流產業發展的指標體系，具體如表1所示。

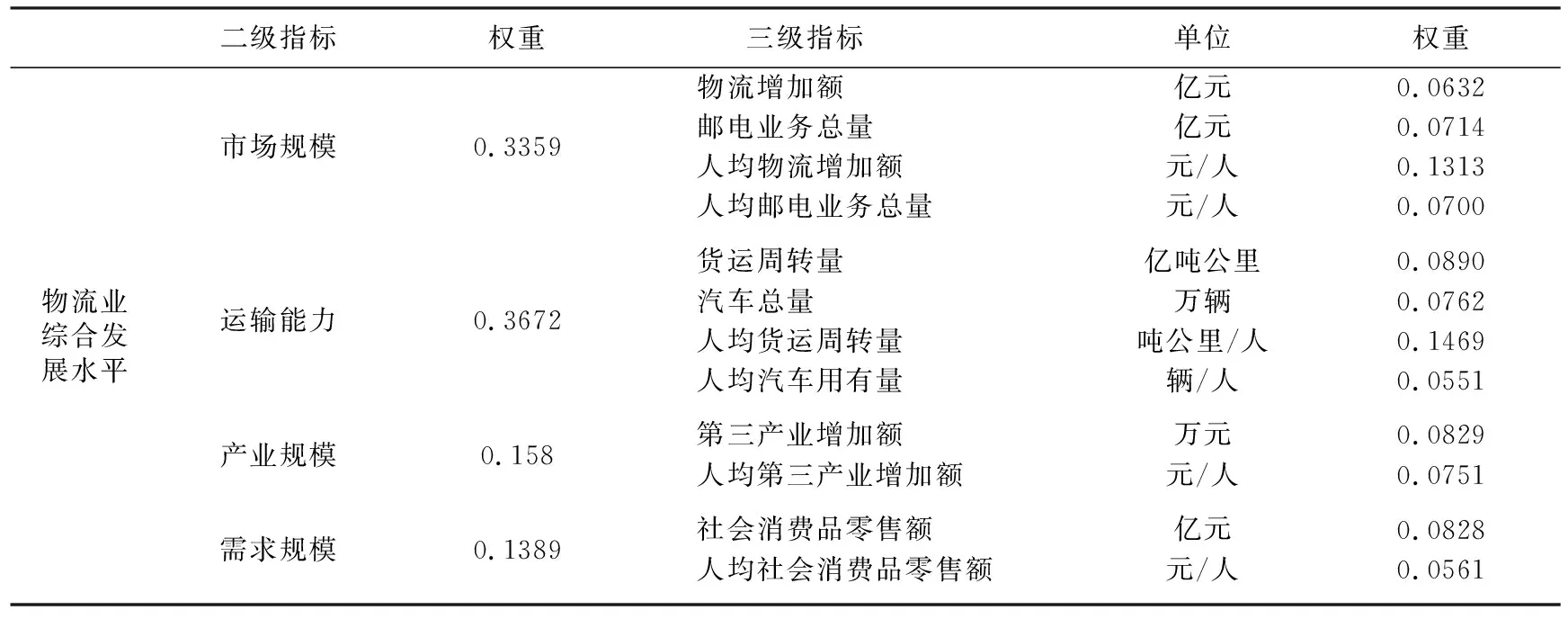
表1 中國省區物流產業發展評價指標體系

表1中，物流增加額包括交通運輸業物流增加值、倉儲物流業增加值、批發物流業增加值、配送加工包裝物流業增加值和郵政業物流增加值；郵電業務總量是指以價值量形式表現的郵電通信企業為社會提供各類郵電通信服務的總數量；物流增加額和郵電業務總量直接反映了產業的市場規模；貨運周轉量是指在一定時期內各種運輸工具運輸的貨物(旅客)數量與其相應的運輸距離的乘積之和；汽車總量是指報告期末已注冊登記領有牌照的全部民用汽車數量與公用汽車數量之和；貨運周轉量和汽車總量反映了區域物流的運輸能力；第三產業增加額是指除第一產業、第二產業以外其它行業的增加額，該指標作為反映宏觀產業發展狀況的“鏡子”，反映了物流業的產業規模；社會消費品零售額是指批發和零售業、住宿和餐飲業以及其他行業直接銷售給城鄉居民和社會集團的消費品零售額，可以直觀反映產業的需求規模。為了消除人口因素的影響，本文將上述各指標除以各省區當年的人口數量之后再納入指標體系。綜上，本文從市場規模、產業規模、需求規模和運輸能力四個方面構建評價省區物流業發展水平的指標體系。

本文用交通運輸、倉儲及郵政業的統計值替代物流產業的相關指標，以2005—2015年中國大陸31個省區作為研究樣本，數據來源于歷年《中國統計年鑒》。

(二)省區物流業發展水平

結合上文構建的指標體系和熵權TOPSIS模型計算出2005—2015年各省區物流產業發展水平得分，具體結果見表2。

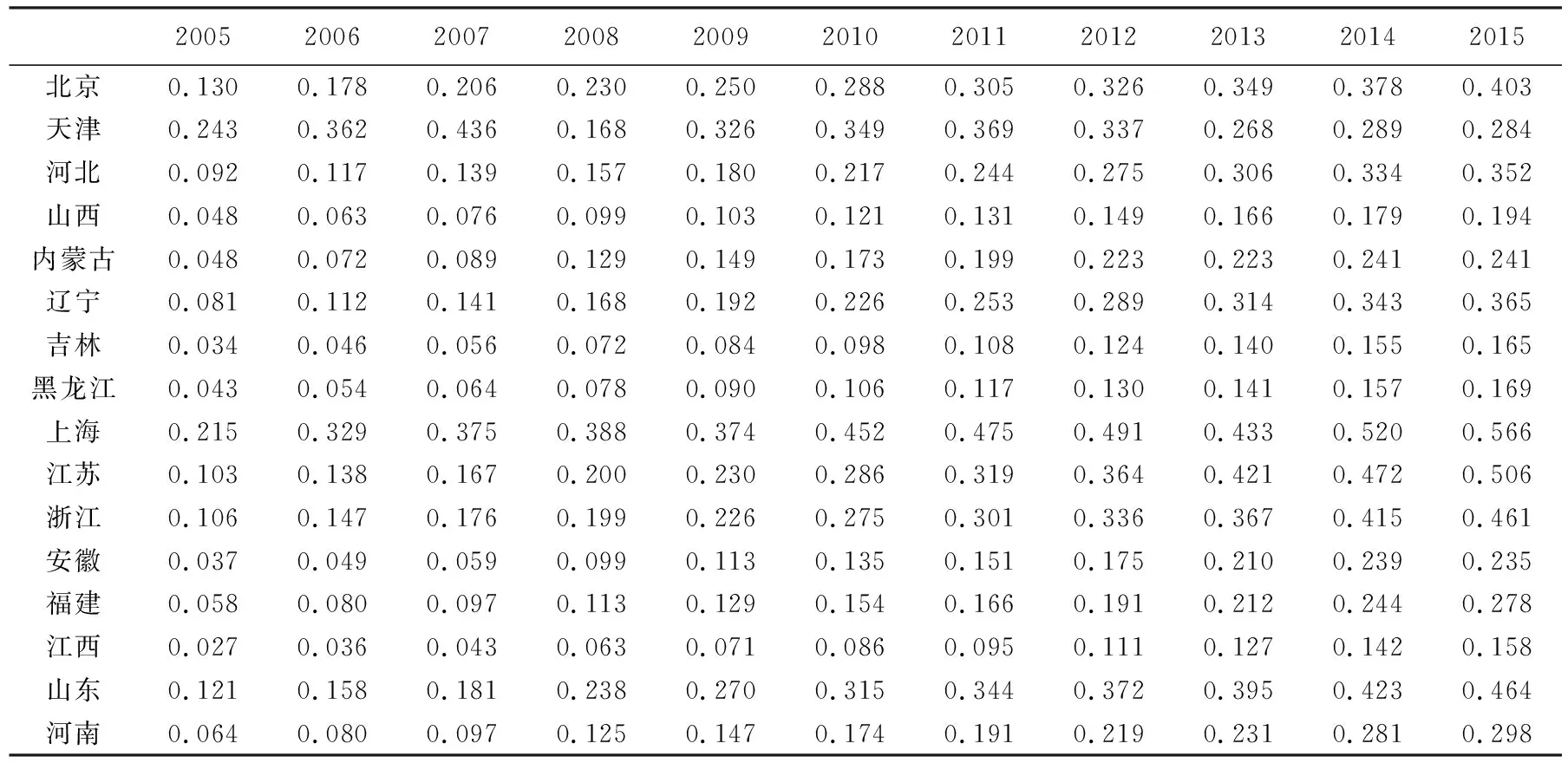
表2 2005—2015年中國省區物流產業發展水平測度結果

(續表2)

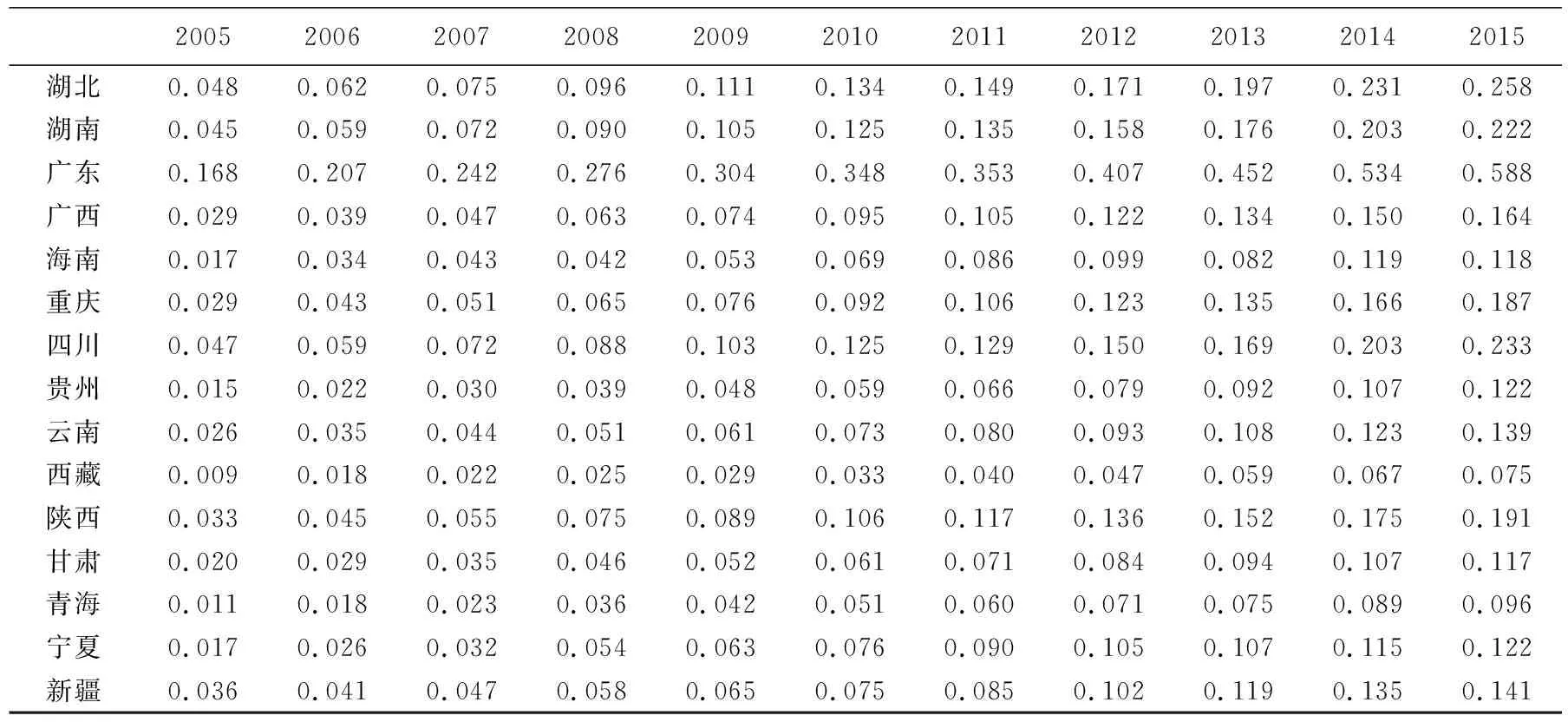
20052006200720082009201020112012201320142015湖北0.0480.0620.0750.0960.1110.1340.1490.1710.1970.2310.258湖南0.0450.0590.0720.0900.1050.1250.1350.1580.1760.2030.222廣東0.1680.2070.2420.2760.3040.3480.3530.4070.4520.5340.588廣西0.0290.0390.0470.0630.0740.0950.1050.1220.1340.1500.164海南0.0170.0340.0430.0420.0530.0690.0860.0990.0820.1190.118重慶0.0290.0430.0510.0650.0760.0920.1060.1230.1350.1660.187四川0.0470.0590.0720.0880.1030.1250.1290.1500.1690.2030.233貴州0.0150.0220.0300.0390.0480.0590.0660.0790.0920.1070.122云南0.0260.0350.0440.0510.0610.0730.0800.0930.1080.1230.139西藏0.0090.0180.0220.0250.0290.0330.0400.0470.0590.0670.075陜西0.0330.0450.0550.0750.0890.1060.1170.1360.1520.1750.191甘肅0.0200.0290.0350.0460.0520.0610.0710.0840.0940.1070.117青海0.0110.0180.0230.0360.0420.0510.0600.0710.0750.0890.096寧夏0.0170.0260.0320.0540.0630.0760.0900.1050.1070.1150.122新疆0.0360.0410.0470.0580.0650.0750.0850.1020.1190.1350.141

表2顯示了2005—2015年中國大陸31個省區的物流產業發展水平。由表2中數據可知，各省區物流產業發展水平存在明顯差異，廣東、上海、江蘇、北京、浙江等地區產業水平較高，并且近年來增長速度較快；新疆、寧夏、青海、甘肅、西藏等地區產業水平較低，且增長速度較為緩慢。總體上，中國物流業呈現出“東強西弱”的發展態勢，各省區物流產業發展的初始水平、發展路徑、發展速度均存在明顯差異。

(三)省區物流業時空演化分析

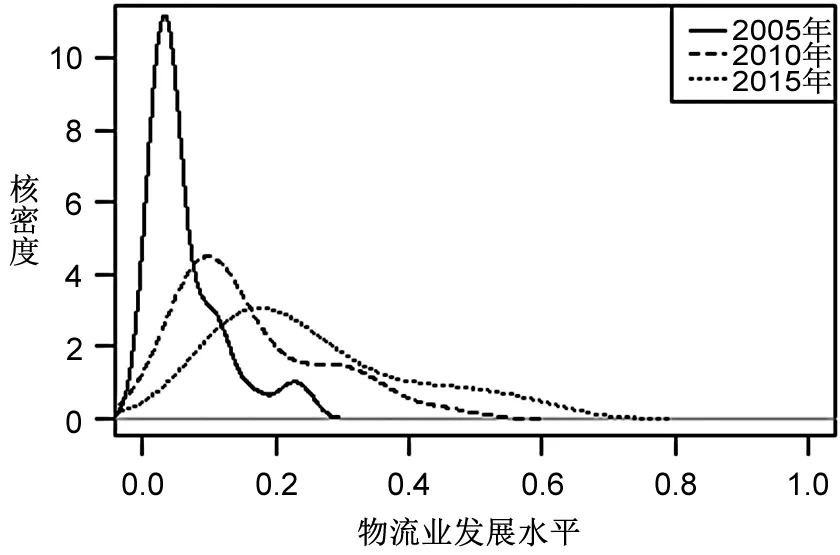
圖1中國物流業發展的核密度分布

(1)物流產業發展的分布狀況。為直觀展現出2005—2015年物流產業整體演化情況，根據表2數據，結合核密度估計結果繪制2005年、2010年和2015年物流業發展水平Kernel密度圖，從而有效呈現產業整體的發展遷移趨勢。具體如圖1所示。

圖1中，2005—2015年密度曲線整體向右遷移，反映出各地區的物流產業發展呈現逐步提升態勢；2005年波峰較陡，呈現出明顯雙峰分布態勢，2010年波峰較為平穩，且雙峰態勢減弱，2015年波峰更為平穩，且波峰已由雙峰分布逐漸轉變為單峰分布，說明產業發展的低位趨同現象出現減弱趨勢；2005年主峰分布在低值與中間值之間，到2015年波峰向右遷移，且波峰下降明顯，說明物流產業發展水平較高地區發展提速放緩，而部分發展中等水平地區發展速度增快。

為展現區域間產業發展差異，進一步繪制出2005—2010年和2011—2015年中國東部、中部、西部地區[注]東部地區包括北京、天津、河北、遼寧、上海、江蘇、浙江、福建、山東、廣東、海南11個省區，中部地區包括黑龍江、吉林、山西、安徽、江西、河南、湖北、湖南8個省區，西部地區包括內蒙古、廣西、重慶、四川、貴州、云南、西藏、陜西、甘肅、青海、寧夏、新疆12個省區。的核密度分布對比圖，具體如圖2所示。

由圖2可知：從位置上看，由第一階段到第二階段，東部、中部、西部三大區域產業發展密度曲線均呈現向右遷移的趨勢，表明各區域的產業發展水平都有所提升；從形狀上看，中部和西部地區的波峰較陡，而東部地區的波峰較為平穩，由第一階段到第二階段中、西部地區的密度曲線形狀變化不大，仍然處于“尖陡”態勢，東部地區則呈現雙峰分布的特點，這說明中西部地區整體發展速度差異不大，而東部地區間的差異較為明顯；從峰值來看，從第一階段到第二階段，三大區域的峰值均明顯下降，這表明區域內部的發展分散化，但區域間的差距仍然明顯。

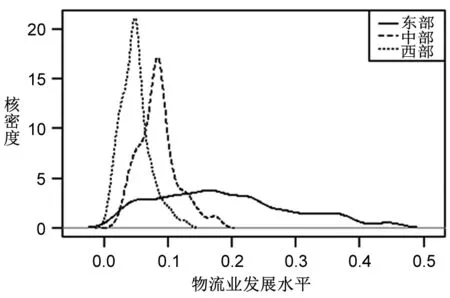
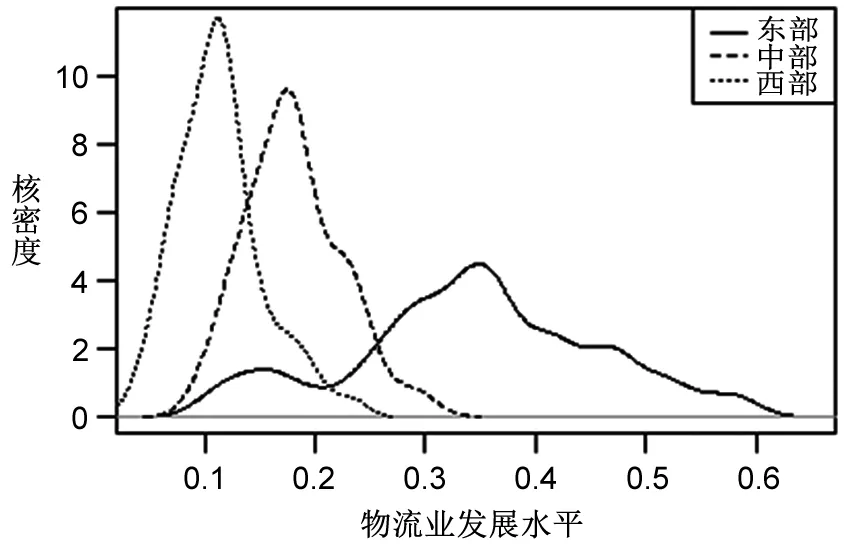
圖2 2005—2010年(左)、2011—2015年(右)中國物流業發展的核密度分布

(2)產業發展的空間相關性。核密度分析顯示了產業發展的區域分布差異，在此基礎上可以利用探索性數據分析方法研究產業發展的空間關聯性。全局Moran指數用于表現整個研究區域物流業發展空間分布特征，可以衡量空間鄰接省區物流業發展水平的相似度。本文利用Geoda軟件，結合式(1)計算各年中國物流產業的全局Moran指數[注]對空間位置進行隨機排列，從而模擬計算出全局Moran指數的P值，即Pseodu p值。本文選擇的排列次數(permutations)為999次。，具體結果如表3所示。

表3 2005—2015年物流產業發展的全局Moran指數統計表

注：***表示在1%的顯著性水平下顯著；Z-value為Z得分。

由表3可知，中國物流業全局Moran指數最小值為2006年的0.3528，最大值為2011年的0.4797；從顯著性水平來看(結合P值和Z得分)，各年Moran值均在1%的水平下顯著，表明中國各省區的物流業發展水平呈現顯著的空間正相關。從時序的角度來看，Moran指數呈現倒“U”型的發展趨勢：2005—2011年Moran指數呈增大趨勢，此時產業發展在空間上的正向集聚區域持續擴大，空間相關性逐步增強；2011—2015年Moran指數呈減小趨勢，此時地理上的局部差異性擴大，相似性減小。

四、物流業驅動因素及其時空異質性研究

由上文分析可知，省區物流業發展差異性與相關性并存，為了進一步甄別物流產業發展演化的驅動因素，需要構建相關計量模型進行探究。Tobler(1970)認為，空間地理位置鄰近地區具有相似的屬性值，地理區位鄰近的區域往往存在空間自相關性，一般不滿足相互獨立的假設，普通全局線性回歸模型的估計將會造成偏差，因而應構建空間計量模型來識別產業發展的驅動因素，分析各因素的時空異質性。

(一)變量選取與指標說明

多數學者(唐建榮 等，2015；王健 等，2014；魏修建 等，2014)將物流總額、物流增加額或者貨運周轉量作為因變量，以此對產業發展的驅動因素進行研究，但由于物流產業受經濟、環境、政治等多方面因素的影響，僅使用物流總額等單一指標難以準確度量其驅動因素。因此，可以利用上文TOPSIS模型評價所得產業發展水平作為因變量，能夠減少單一指標作為因變量可能產生的信息失真問題。

在自變量的選取上，本文利用PEST分析框架，從政治、經濟、社會和技術四個方面總結出影響物流產業發展的因素：

(1)政治因素。進出口貿易和外商直接投資可以作為影響物流業發展的政治因素。對外貿易能夠從需求端拉動物流產業發展，并通過“乘數”作用產生連鎖反應；同時，外商直接投資可以發揮中國市場、資源和勞動力方面的比較優勢，從而提高物流業的發展效率。本文用各地區人均進出口貿易總額(按經營單位所在地分)代表進出口貿易水平(ie)(唐建榮 等，2017)，以人均外商直接投資總額(fdi)代表外商直接投資水平(姚娟 等，2012)。

(2)經濟因素。經濟發展可以改善產業結構、分配結構、消費結構，進而促進區域間的資本、要素的流通；同時通過影響用戶消費偏好，促進物流服務業的發展。人均gdp是衡量區域經濟運行狀況的晴雨表，因此使用省區人均gdp代表其經濟發展狀況(唐建榮 等，2017)。

(3)社會因素。人口因素，即勞動力數量的增加會為產業發展帶來“人口紅利”；基礎建設可以提高既有資源的整合水平和利用程度，實現不同區域主體間的要素流動和功能整合，發揮產業發展網絡擴散的正外部性。本文以物流業從業人員數代替物流產業的勞動力投入水平(lab)(陳恒 等，2015)，用物流網絡密度(鐵路與公路營業里程之和比上區域國土面積)代表基礎建設水平(王健 等，2014)。

(4)技術因素。科技發展縮短了用戶和服務商之間的距離，提高了商品流通速度，增加了物流配送需求，降低了企業產品和服務的成本，提升了服務質量。研發(rd)經費內部支出可以較好地反映區域科技發展程度。因此，本文用人均研發(rd)經費內部支出反映地區科技水平。

綜上，本文選取進出口貿易、外商直接投資、經濟發展、勞動力投入、基礎建設、科研投入作為產業發展的驅動因素。數據來源于歷年《中國統計年鑒》，為了避免殘差的異方差性帶來的影響，對上述數據均進行自然對數轉換(以e為底)。各變量的描述性統計結果見表4所示。

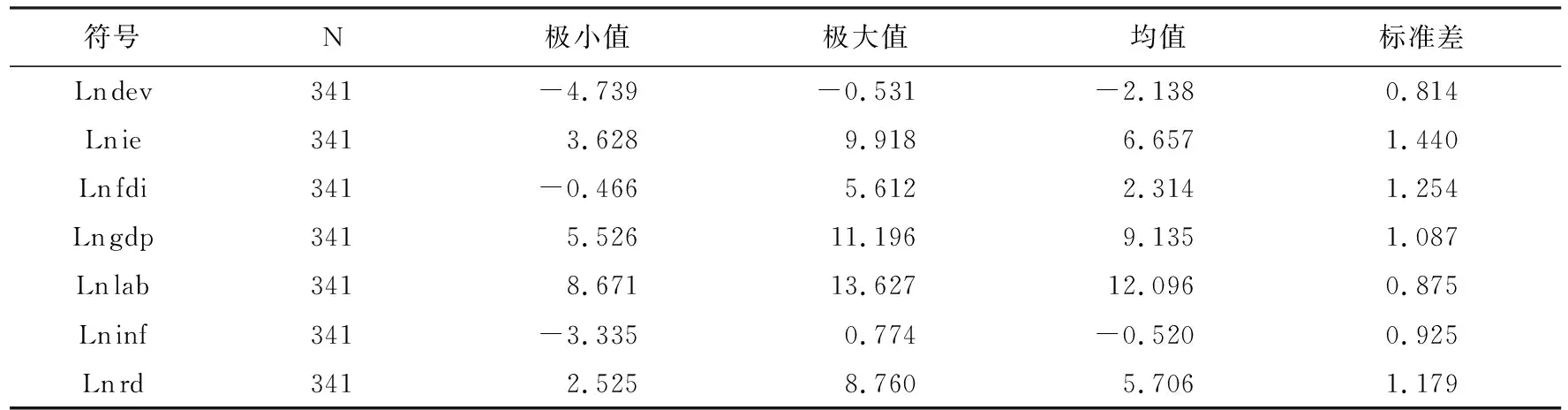
表4 變量的描述性統計結果

(二)單位根與多重共線性檢驗

為了避免偽回歸情況的出現，本文采用ADF和PP兩種單位根檢驗方法確定數據的平穩狀況。此外，利用方差膨脹因子(Variance Inflation Factor，VIF)檢驗各變量之間是否存在多重共線性(姚昕 等，2017)，具體結果見表5所示。

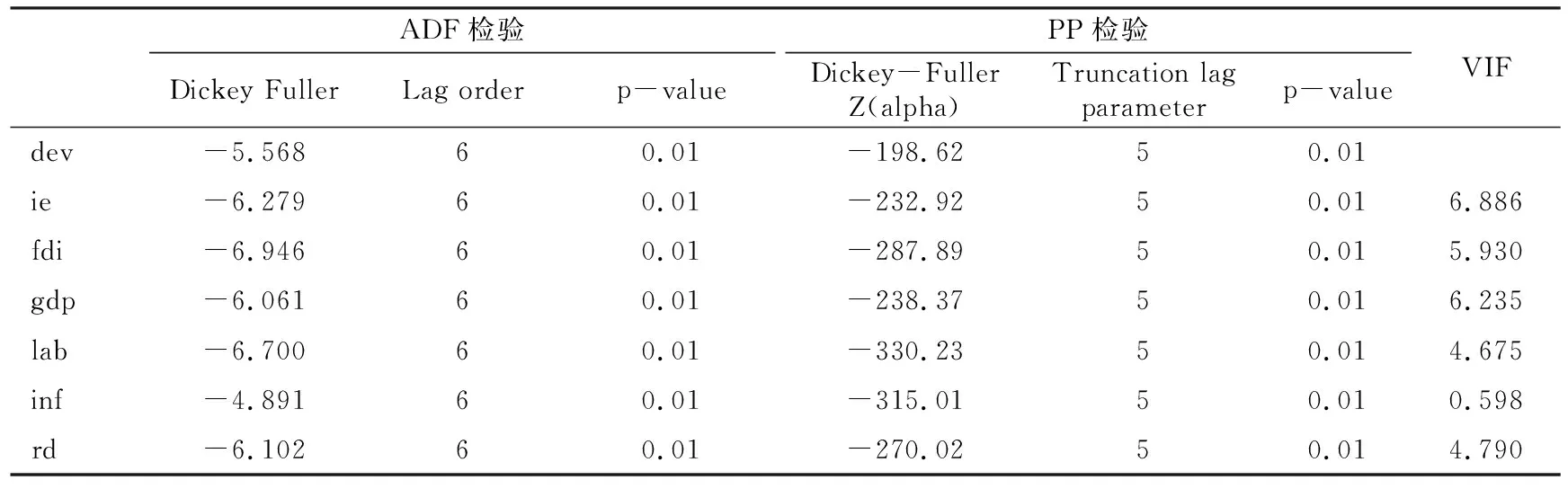
表5 各變量的單位根檢驗和VIF檢驗結果

注：表中的Dickey-Fuller為迪基-福勒檢驗值，Lag order為滯后長度，結果由R軟件計算所得。

由表5可知，不論是ADF單位根檢驗還是PP單位根檢驗，均在1%水平下顯著地拒絕數據不平穩的原假設，因此所有變量都是平穩的，適合進行面板數據回歸建模。同時，各變量的方差膨脹因子均小于經驗值10，因此變量之間不存在多重共線性。

(三)物流業驅動因素的實證結果與分析

GTWR模型能估計自變量在時空演變中的局部效應，其參數估計值隨著時空的演變而不同，從而可以揭示驅動要素的時空異質性。為了保證回歸結果的有效性和穩健性，在進行GTWR回歸之前，要先做普通面板回歸，結果見表6。

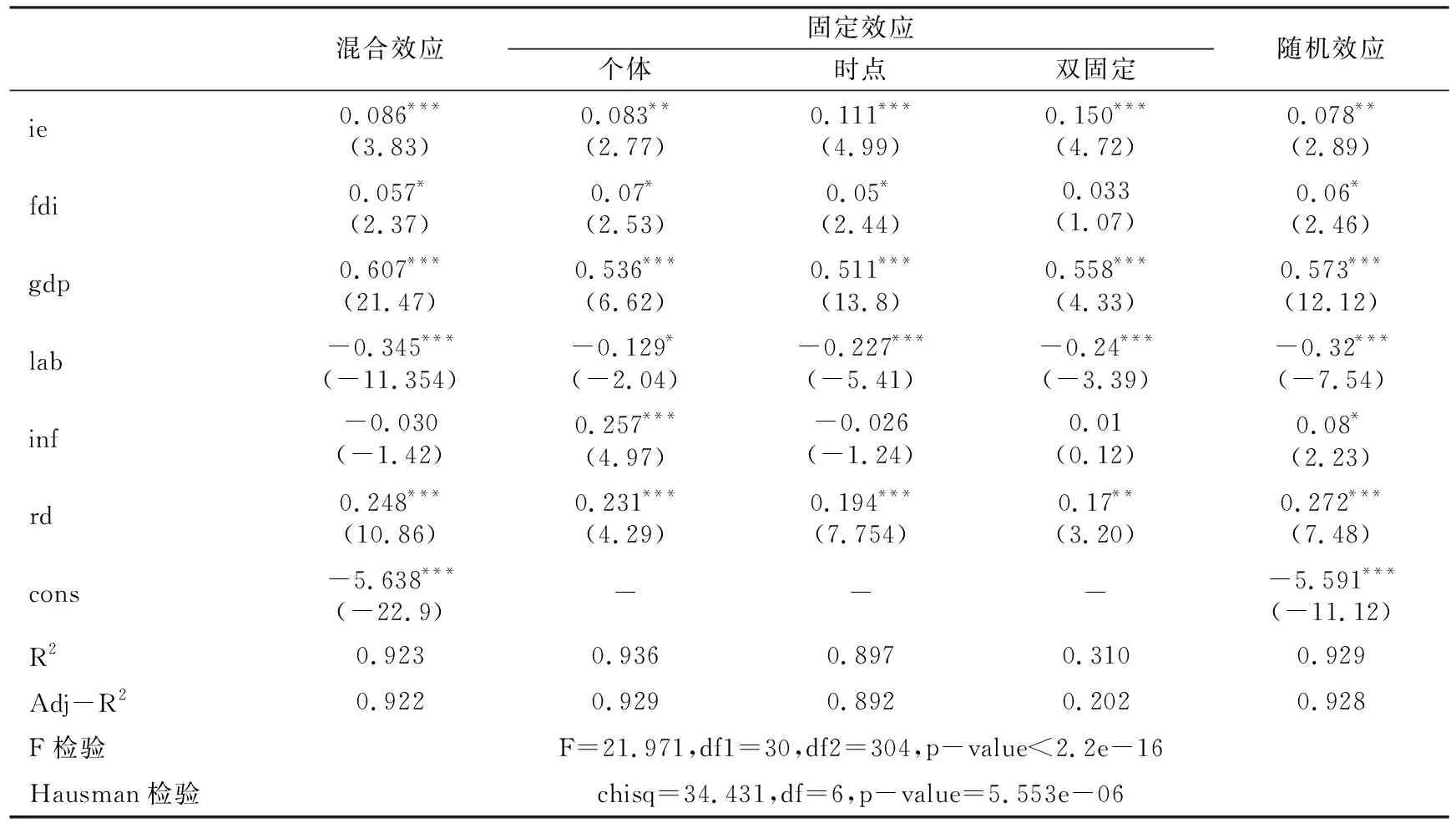
表6 普通面板數據回歸匯總

注：括號內數字為t統計值；*、**、***分別表示在10%、5%、1%的水平上顯著。

由表6可知，F檢驗的P值小于1%，拒絕了建立混合模型的原假設；Hausman檢驗的P值小于1%，拒絕了建立隨機效應模型的原假設，這表明應采用固定效應模型。從固定效應模型的回歸結果來看，個體固定效應模型的解釋力最強，說明個體間的差異較為顯著，經濟發展、基礎設施建設、研發投入、進出口水平及外商直接投資對物流產業的正向影響依次減弱，勞動力因素的影響為負。值得注意的是，勞動力投入系數在各種效應下均為負，表明物流產業的勞動密集性特征已逐漸弱化，過多的勞動力聚集可能會由于要素競爭阻礙產業的發展，或表明地區勞動力效率并不高，這也印證了陳恒等(2015)的觀點，即勞動力規模擴大并不能有效驅動物流業發展。

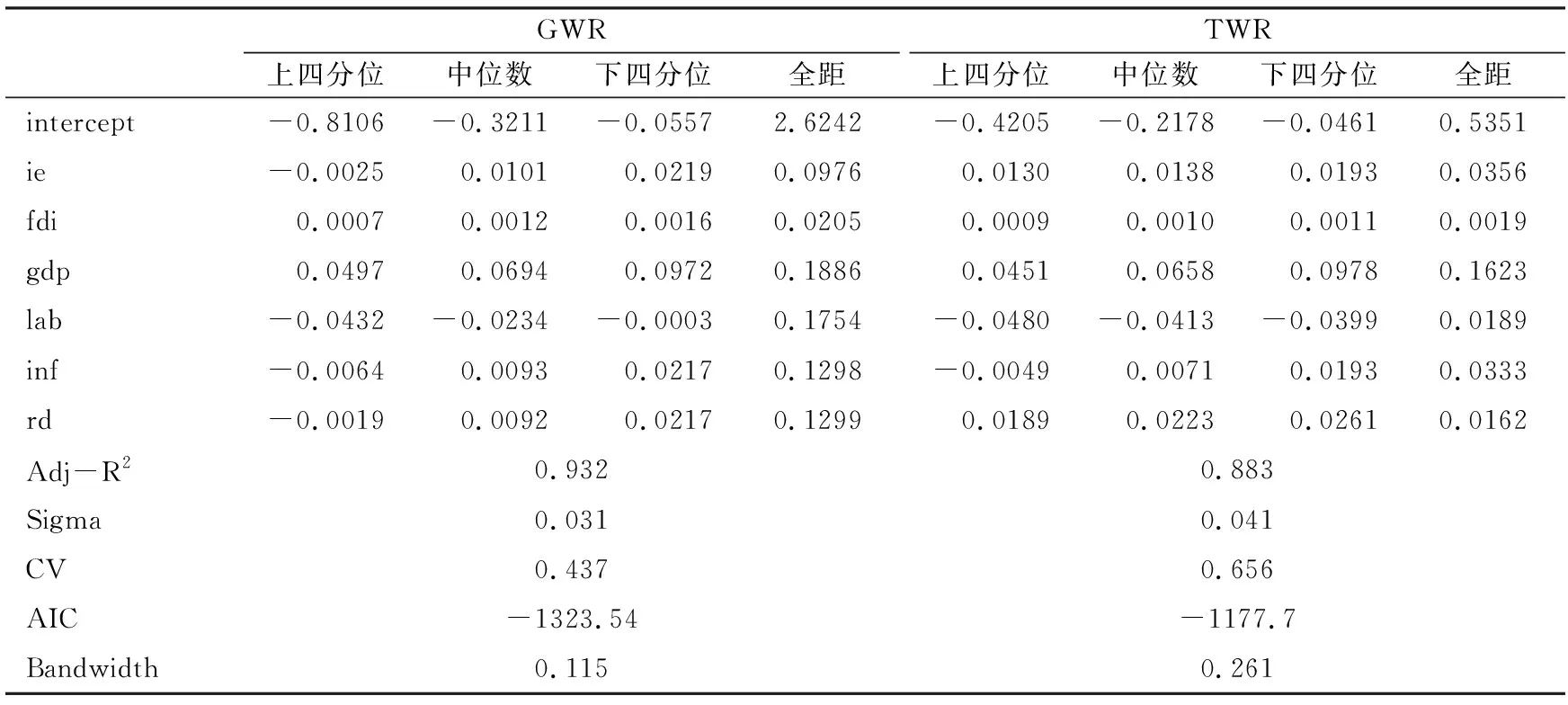
表7 2005—2015年各要素的GWR及TWR估計結果

注：回歸結果由Arcgis10.3.1軟件結合GTWR Beta1.0工具箱計算得到，該工具箱由香港中文大學開發提供。

普通面板回歸一定程度上反映了各要素的作用強度，但并未考慮空間距離因素，因此不同觀察值間的差異被平均了，只能得到一個整體的相互依賴關系，不能反映參數在不同空間的非穩定性(齊亞偉 等，2014)。因此，本文從時間、空間角度構建局部加權回歸模型進行參數估計，并利用高斯核函數法構建權重矩陣，同時結合交叉驗證法CV、AIC測算最優帶寬[注]在GWR模型中，若帶寬趨于無窮大，任意兩點的權重將趨于1，則被估計的參數變成一致時，GWR就等于經典的OLS線性回歸；反之當帶寬變得很小時，參數估計將會更加依賴于鄰近的觀測值。，最終得到GWR、TWR模型的估計結果(具體見表7)。

表7呈現了GWR和TWR的回歸結果，根據CV、AIC及調整的R2進行綜合判斷，GWR的解釋力強于全局線性回歸結果，也強于TWR的估計結果(AIC、CV值越小，表示模型的解釋力越強)。在GWR模型中加入時間因素構建GTWR模型，從而得到參數估計結果，具體見表8所示。

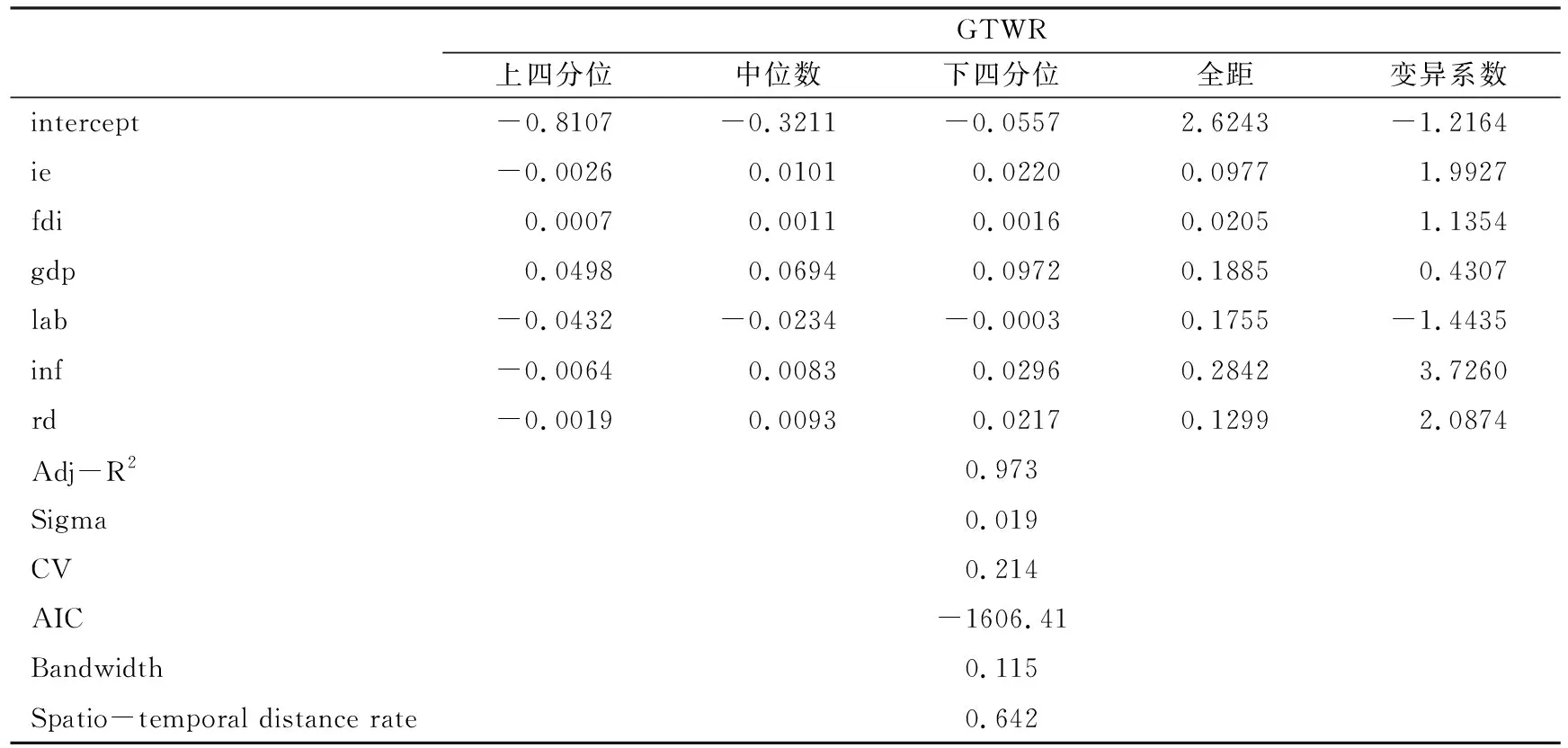
表8 2005—2015年各要素的GTWR估計結果

注：相對于GWR和TWR模型，GTWR模型從時間、空間兩個維度同時進行考察，故表中提供了Spatio-temporal distance rate的數值；變異系數反映了系數的波動幅度，其計算公式為：變異系數(CV)=標準偏差(SD)/平均值(Mean)。

表8報告了GTWR模型的估計結果。對比表7可知，三種局部回歸模型的估計結果都在相應區間內波動，波動強度存在一定的差異。這可能是因為不同的模型關注了不同方面的非平穩性。從擬合度、CV和AIC等結果來看，GTWR模型調整的R2值達到0.973，CV、AIC值分別為0.214、-1606.41，表明該模型的擬合優良性全面優于GWR、TWR模型，因而綜合考慮時間和空間因素的GTWR模型為最優選擇。

為了更加清楚地揭示驅動要素的波動情況，接下來從回歸系數總體分布、空間差異、時序波動三個方面進行探討。

(1)系數的總體分布。基于GTWR回歸結果，繪制出各變量系數的密度圖[注]GTWR模型綜合考慮時間和空間信息進行參數估計。N×T的回歸樣本可得到N×T個系數，本文樣本數量31×11，可得到341個估計系數。限于文章篇幅，各年不同地區的參數估計值不再一一列出，具體結果在圖3中進行展示。，具體如圖3所示。

由圖3可知，不同變量系數的分布存在較大差異。其中，ie的系數分布較為對稱，高峰位于0.01左右，說明進出口貿易作用于產業發展呈現出較為顯著的梯度特征，即對于不同地區的驅動力存在較大差異，對部分地區的產業發展甚至存在抑制作用；fdi的系數呈現明顯的右偏尖峰分布，峰值位于0.001前后，表明外商直接投資對各地區產業發展存在正向驅動作用，呈現出強度小、穩健性高、變異性低的特征；gdp的系數均為正值，且總體呈右偏分布，峰值約為0.05，表明經濟發展能有力推動地區物流產業發展；lab的系數值正負不一，峰值位于-0.025左右，說明勞動力數量對于多數物流產業發展的作用為負，且地區間系數也存在較大差異；inf的系數呈現明顯的左偏分布，峰值接近于0，說明基礎設施建設對于區域產業發展的促進作用較小，甚至存在一定程度的抑制作用；rd的系數呈多峰分布態勢，主峰值約為0.01，表明研發投入對于大部分地區的產業發展具有明顯促進作用，對部分地區的驅動作用較強。

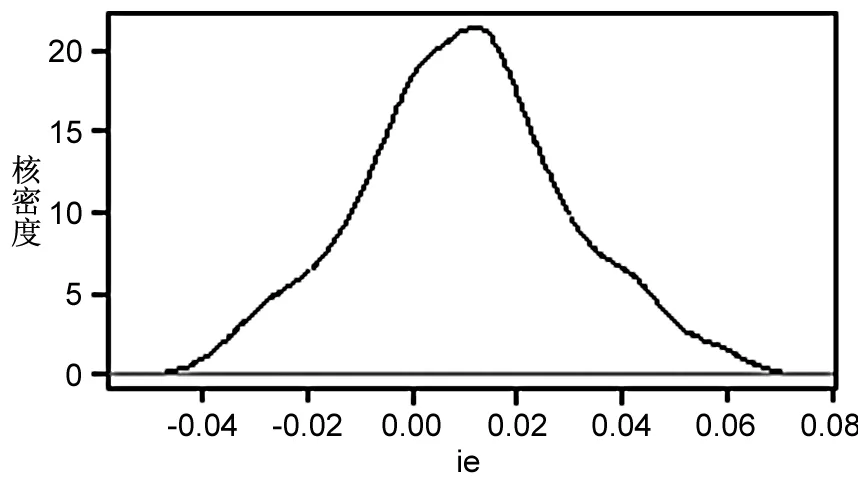
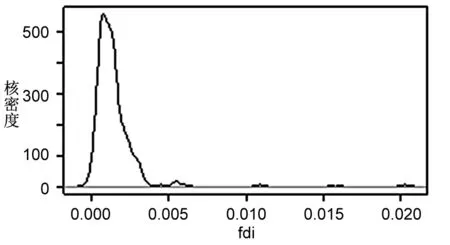
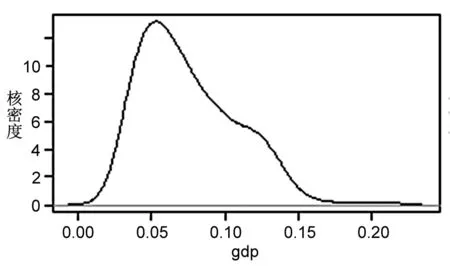
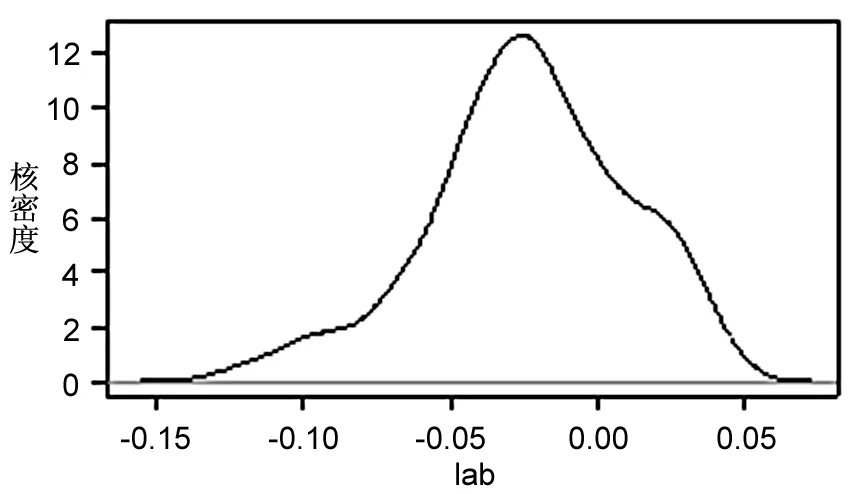
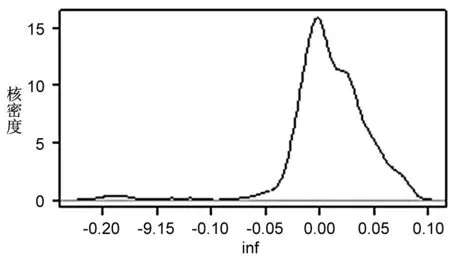
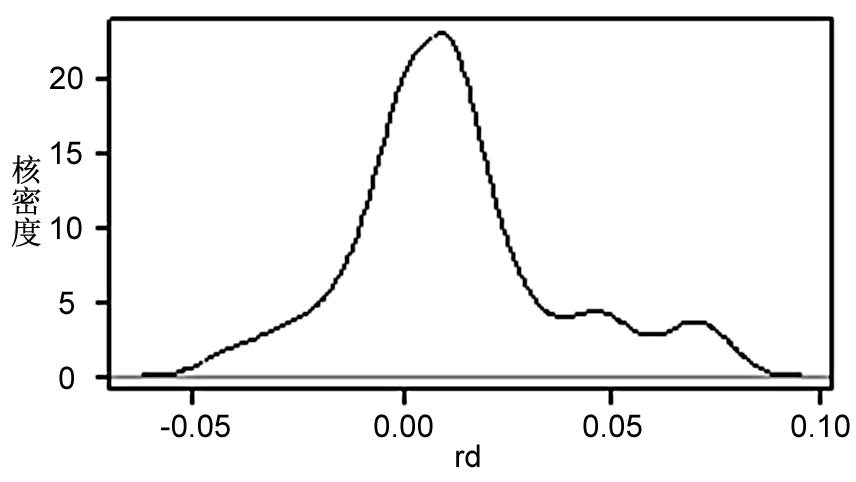
圖3 各要素回歸系數的分布密度圖

(2)系數的空間差異。利用GTWR模型年均局域估計結果，結合Arcgis10.3.1軟件對各要素系數的地區分布情況進行可視化處理，采用自然斷點分類法(Natural Breaks Jenks)將相似性最大的數據分在同一級(劉華軍 等，2016)，差異性最大的數據分在不同級，從而可以在空間上分析各驅動要素的差異性，具體結果如圖4、圖5、圖6所示。

由圖4—圖6可知，對于不同區域而言，各變量的分布存在明顯差異：

關于ie系數的空間分布。由圖4(左)可知，ie系數的空間分布總體呈現東低、中高、西低的格局。東部地區尤其是長三角地區處于貿易活躍區，港口物流貿易較為發達，進出口貿易已達到一定規模，繼續通過進出口貿易促進產業發展的收益有限，甚至會出現邊際效應遞減現象；中部地區地處交通要塞，擁有物流網絡核心的地位，該地區ie系數較高，其貿易規模仍有進一步提升的空間；西部地區經濟活力較低，貿易規模較小，其作用系數也較低。

關于fdi系數的空間分布。由圖4(右)可知，外商直接投資系數的空間分布總體呈現“東中部地區低、西部地區高”的特點。擴大外商直接投資規模可以拓展經濟范圍，減少交易成本，提高中國整體物流從業者的相對工資水平。相對于東部地區等產業“富饒區”而言，西部地區外商直接投資能夠更好地促進勞動力、資本等要素的流入，增強地區經濟活力，促進產業的發展；同時，還能顯著提高工農業領域的貨物周轉水平(姚娟 等，2012)。西部地區制造業基礎較好，因此外商直接投資在該地區的作用系數也較高。

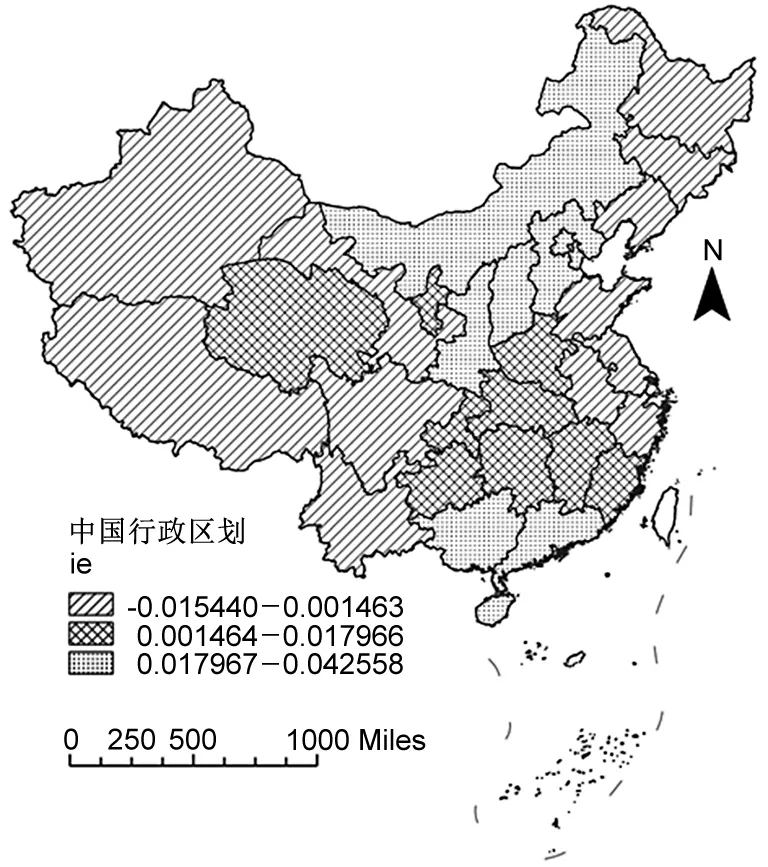
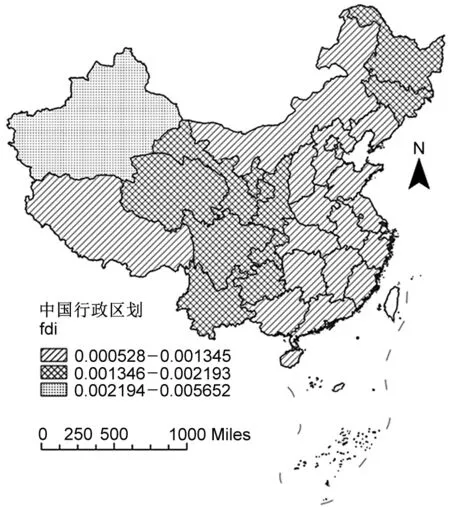
圖4 ie和fdi平均作用的空間分布圖

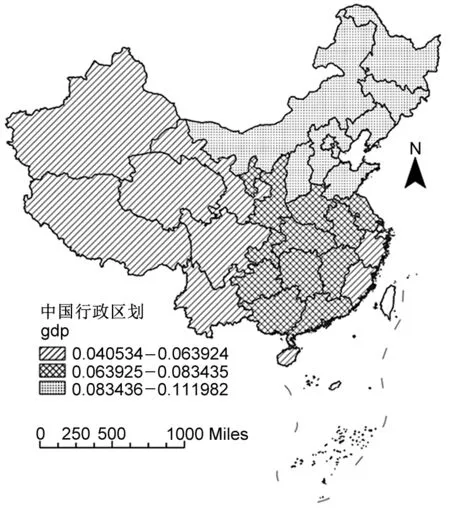
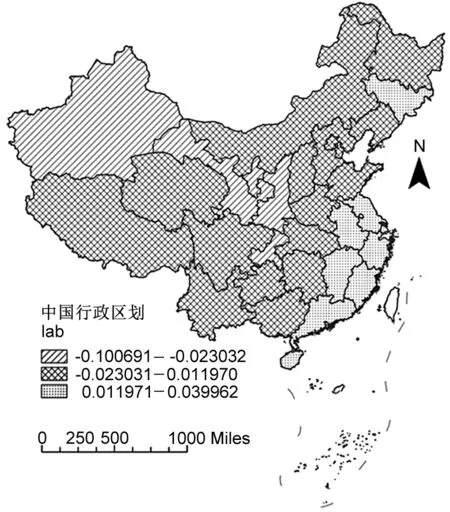
圖5 gdp和lab平均作用的空間分布圖

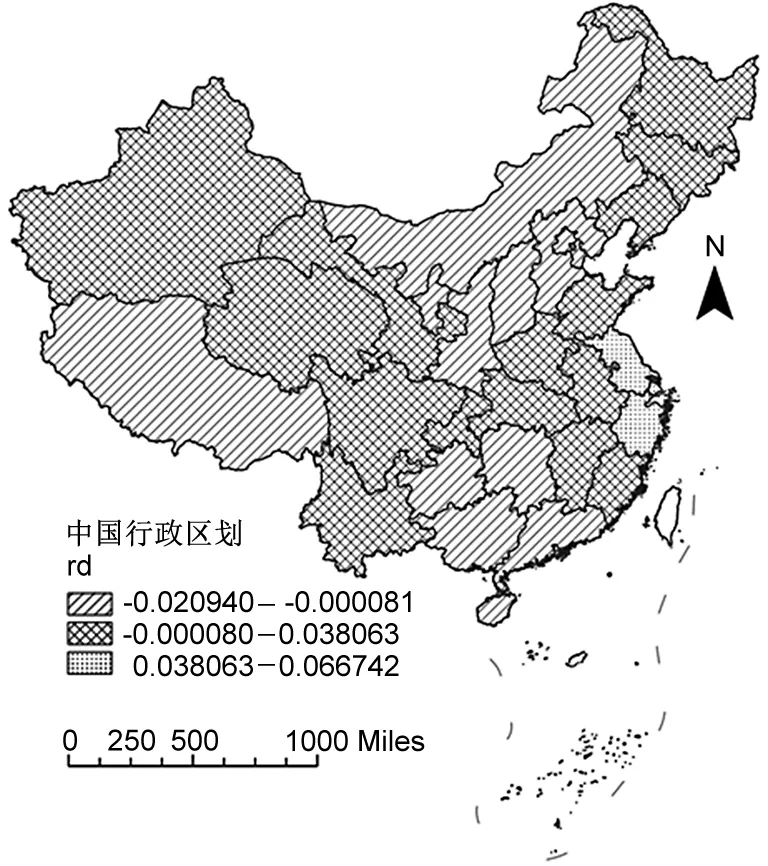
圖6 inf和rd平均作用的空間分布圖

關于gdp系數的空間分布。由圖5(左)可知，gdp對各地區物流業發展均具有正向作用，物流業的需求量依賴于地區經濟的發展。gdp對中部地區物流產業的作用系數較高，對西部地區的作用強度較低，表明區域經濟發展存在不均衡的現象：即區域間經濟發展差距過大，缺乏聯動性，使得資源要素產生集聚，從而導致產業發展存在“馬太效應”；區域內經濟與基礎建設、科技研發等要素發展的“不配套”，協同度較低，從而導致部分地區經濟驅動力較弱。

關于lab系數的空間分布。由圖5(右)可知，勞動力投入系數呈現出“東部-中部-西部”的梯度遞減分布。這表明勞動力投入對于東部地區物流產業發展具有較強促進作用，對西部地區的促進作用較小，甚至存在反向抑制作用。隨著物流產業的快速發展，物流從業人員的工作范圍已從過去的運輸和倉儲等低端領域向物流信息系統開發、物流系統規劃、第四方物流管理等領域拓展(鄔躍 等，2007)。物流產業勞動密集型的特征正在變弱，技術密集型的特點開始凸顯。在此背景下，市場對勞動力的要求逐漸由“量”轉為“質”。東部地區作為人才的聚集地，高端人才較多，可以較好地滿足產業發展需求；西部地區物流人才缺乏，勞動力“量”的提升并不能滿足產業發展需要，反而會因惡性競爭抑制產業發展。

關于inf系數的空間分布。由圖6(左)可知，基礎設施建設的系數呈現出由南向北梯度遞減的規律，表明隨著區位的北移，基礎設施建設的促進效果減弱，甚至出現系數為負的情況。在GTWR模型中，特定區域的回歸參數不再是利用所有樣本估計的假定常數，而是利用其鄰近區域的子樣本信息進行局域回歸估計，并隨時空位置的變化而對參數進行調整。區域物流產業的發展同時受到該地區及鄰近地區基礎設施建設的影響，跨地區交通基礎設施的建設往往會擴大發達地區對落后地區各類生產要素的“虹吸效應”，進而導致基礎設施建設的負向溢出(張學良，2012)。當這種負向溢出效應大于其鄰近地區基礎設施建設的正向擴散效應時，則會出現系數為負的情況。歸根到底，這是由于鄰近地區間產業發展協同度不高，地區差異過大所導致的。

關于rd系數的空間分布。由圖6(右)可知，東部沿海地區的研發投入系數較高，南部地區、北部地區的系數相對較低，部分地區的系數為負，從而產生了“創新悖論”的現象[注]創新悖論指創新不一定能有效地轉化為增長(Pessoa et al.，2010)。(Pessoa et al.,2010)。從“社會過濾”[注]社會過濾用于描述本地經濟社會條件對創新轉化為增長所產生的“過濾”作用，本地經濟社會條件就好比創新與增長中間的“介質層”，“介質層”的不同導致創新轉化率也不同(Rodriguez-pose et al.，1999)。的角度來看，各地區的產業基礎、經濟條件并不相同，導致其社會過濾能力也不盡相同。而社會過濾對于創新的有效轉化兼具促進和抑制兩種作用，這兩種作用的對沖及消長可能是科技投入轉化物流產業增長之間的黑箱。從區域協調發展的角度來看，鄰近地區之間科技水平或者產業發展差距過大，可能導致科技創新系數為負的情況。因此，系數較高的地區，表明其社會過濾能力較強，創新轉化效率較高；系數較低的地區，表明其社會過濾能力較差。值得注意的是，系數為負不一定是要求地區減少相應的科技投入，而是在政策含義上意味著注重區域投資實踐中效率與數量的均衡。

(3)系數的時序變動。為展現各要素的時序波動情況，本文繪制出各要素驅動系數時序波動圖，橫軸代表不同年份(2005—2015年)，縱軸表示變量的系數大小，具體見圖7—12所示。

由圖7可知，ie系數的時序波動大致可分為上升型和波動型。其中，波動型的地區包括黑龍江、遼寧、吉林、廣西、重慶、四川、貴州、云南、西藏、陜西、甘肅、青海、寧夏、新疆等省區，其余省區為上升型。波動型區域應根據不同階段的實際市場需求來確定進出口貿易目標，使得進出口貿易規模與物流產業發展實力相匹配；上升型區域由于市場需求尚未飽和，可以加強進出口貿易以帶動當地物流業的進一步發展。

由圖8可知，fdi系數的時序波動大致可劃分為三類：上升型、下降型、波動型。其中，上升型的地區包括湖南、廣東、廣西、海南、重慶、四川、貴州、云南等南方省區；波動型地區的有西藏、陜西、甘肅、寧夏、新疆等西北部省區，其余省區為下降型。上升型區域應繼續加大外商投資力度；下降型地區應適度把握外商直接投資規模，基于地區發展潛力和償債能力合理引進外資；波動型區域應強化外商直接投資的“利用效率”和溢出效應。

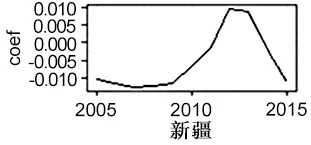
圖7 ie系數的時序波動情況

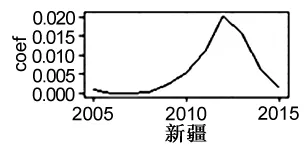
圖8 fdi系數的時序波動情況

由圖9可知，gdp系數的時序波動基本呈現出逐年增長態勢，不同地區的增長速度略有不同，這表明經濟發展水平是區域物流業發展的核心驅動力，且驅動作用日益增強，但地區間動力演化存在顯著的差異性。

由圖10可知，lab系數的時序波動可分為三種類型：“下降-上升型”、“上升-下降-上升”型、下降型。其中，“下降-上升”型包括北京、天津、河北、山西、內蒙古等省區；“上升-下降-上升”型包括遼寧、吉林、黑龍江、上海、江蘇、浙江、安徽等省區；其余省區為下降型。值得注意的是，2008—2009年間三種類型地區勞動力系數都呈現出明顯的下降趨勢。這是由于2008年經濟危機先影響到中國進出口貿易，進而導致物流產業發展出現停滯，多數地區物流業勞動力供求出現失衡，從而表現出其作用系數呈現顯著衰減的特征。

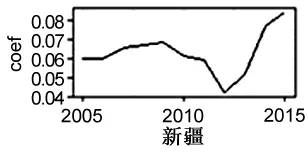
圖9 gdp系數的時序波動情況

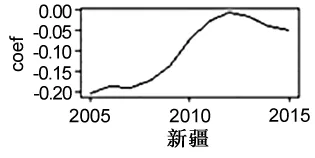
圖10 lab系數的時序波動情況

由圖11可知，inf系數的時序波動呈現出“兩極分化”的現象：華東地區、華北地區(包括北京、天津、河北、山西、內蒙古、遼寧、吉林、黑龍江、上海、江蘇、浙江、安徽、福建、江西、山東、河南等省區)的系數呈持續上升的態勢，并逐漸由負數轉變為正數；華南、西北等地區的系數表現為逐漸下降或先上升后下降的態勢。說明華東、華北等地區物流基礎設施建設的協同度和聯動性較好，跨地區基礎設施的“虹吸效應”出現逐漸減弱趨勢。

由圖12可知，rd系數的時序波動可分為三種類型：上升型、下降型、上升-下降型。其中，上升型包括重慶、四川、云南、甘肅、青海、新疆等省區；下降型包括北京、天津、河北、山西、內蒙古、山東、河南、湖北、湖南、廣西、海南、貴州、西藏、陜西、寧夏等省區；其余省區屬于先上升后下降型。上升型地區的科研投入可以較好地促進該地物流產業的進步；下降型地區的研發投入對于當地產業促進作用呈現逐漸減弱態勢，可能是由于當地社會過濾能力較弱或邊際效應遞減所致；先上升后下降型地區的研發驅動系數也呈現出一定的邊際遞減效應。

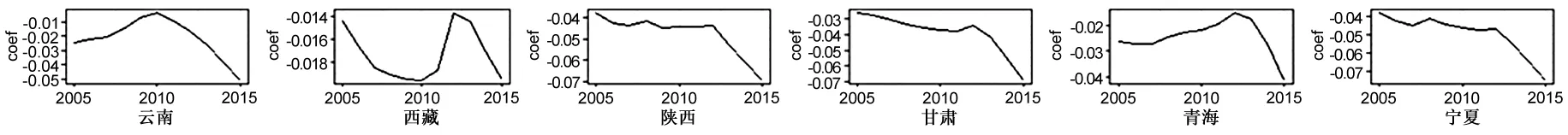
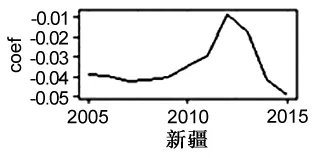
圖11 inf系數的時序波動情況

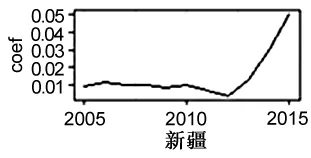
圖12 rd系數的時序波動情況

五、結論與建議

基于2005—2015年中國省級面板數據，運用TOPSIS模型測度省區物流業發展水平，并結合核密度估計、探索性數據分析研究物流產業演化規律，通過構建GTWR模型考察物流產業發展的驅動因素及其時空異質性。研究結果表明：中國省域物流業發展差異性與相關性并存；物流產業多維驅動要素呈現出明顯的時空非平穩性，不同時點、不同地區各驅動要素的波動方向和作用強度并不相同；不同驅動要素分別呈現出左偏、右偏、對稱、多峰等分布態勢；各要素均呈現出一定的東、中、西梯度分布格局；不同地區各驅動要素的時變形態不同。

為了促進區域物流業的協同健康發展，接下來從區位差異、驅動異質、動力演化三個層面提出對策建議，以破解中國物流業發展區域失衡的困境：

(1)區域協同，穩健驅動。地區產業發展差距過大是造成驅動要素波動的重要原因。因而，應首先在政策導向上建立跨區域協調機制，加大對物流產業發展弱勢區的扶持力度，加強跨區域產業協作，促進區域流通資源優勢互補，縮小地區間產業發展差距。此外，要從各要素本身出發，提高其驅動力的穩健性。比如提高創新轉化效率，加速區域間的知識溢出、技術擴散；完善交通樞紐設施的共建共享，加強支線與干線的互聯互通，優化運輸方式連接路徑，弱化基礎建設的負向溢出效應；合理分配區域勞動力投入，提升勞動力效率；縮小地區經濟貧富差距，建立區域間經濟聯動機制。

(2)因地制宜，精準驅動。針對不同地區要素驅動效應的異質性，應根據各區域在空間關聯中的不同地位和作用以及產業增長板塊的不同功能，選擇有針對性的區域產業政策，進行定向調控和精準調控，以優化產業發展的空間配置效率、提升區域物流產業發展的空間協同性。要因地制宜地走集約化、錯位化的產業發展道路，形成各地區優勢互補、產業錯位、合理分工、聯動發展的產業發展新格局。依托相對優勢，提升產業發展水平和綜合實力，進一步實現中國物流業的跨越式發展。

(3)動態迭代，多元驅動。不同時期，各地區物流產業驅動力會產生迭代和遷移。因此，要結合各地區產業發展的動力轉換機制，實時調整產業驅動策略，以適應不同時點各區位產業發展的獨特要求；要實現不同驅動力之間的動態、多元組合，并形成合力，以提升要素驅動效率。同時，應在科技水平、經濟發展、基礎建設和勞動力等要素驅動的基礎上，繼續探尋產業發展的新驅動，構建全新的多維度、立體式驅動網絡，進一步釋放產業活力，推動物流產業持續健康發展。