從高考試題例說課本的教學
2019-02-19 08:05:18徐建平
數理化解題研究 2019年6期
徐建平
(陜西省西安市第八中學 710000)
一、例說課本中概念、法則、定理的教學
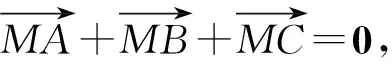
A. 2 B. 3 C.4 D. 5
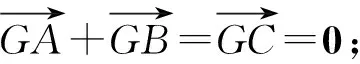
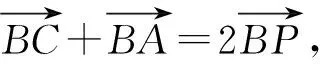

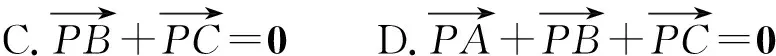
解析若對結論2很熟悉,逆用結論2直接選B.下面給出一組試題,請同學們一試.
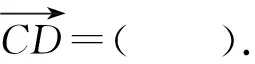


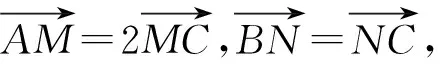
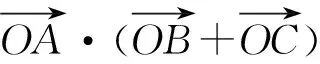
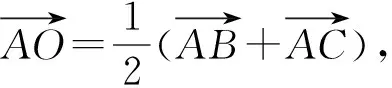
二、例說課本中例題的教學
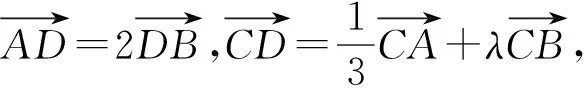
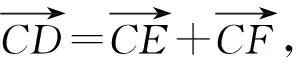
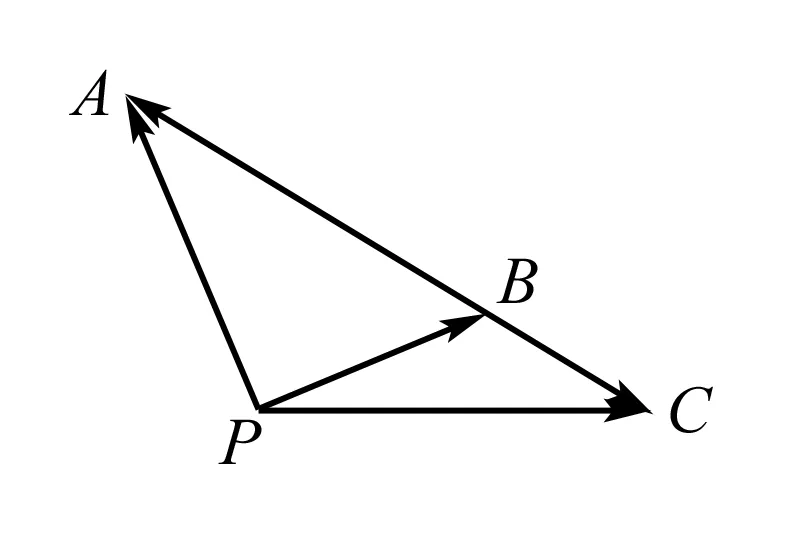
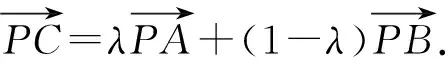
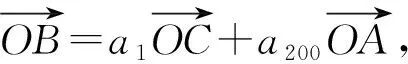
A.100 B.101 C.200 D.201
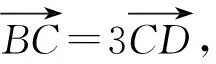
A.x+y-2=0 B.2x+y-1=0
C.x+2y-2=0 D.2x+y-2=0
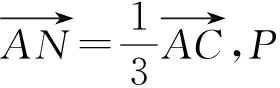
(以上各題的答案為:1.A;2.A;3.A;4.B)
三、例說課本中習題的教學
課本是我們學習的根本,對課本中的習題,我們不能只要求學生會解,更要培養學生的探索意識、創新能力,要能挖掘習題所蘊含的一些重要結論、方法、技巧,并能將這些結論、方法、技巧用于解題中,讓學生從中領略數學的魅力,體會數學學習的樂趣.下面僅舉一例說明之.
高中數學必修4(北師大版)習題1-6 B組1.在同一直角坐標系內畫正弦函數y=sinx和余弦函數y=cosx在區間]0,2π]上的圖象,并回答下列問題:(1)寫出滿足sinx=cosx的x的值;(2)寫出滿足sinx>cosx的x的取值范圍;(3)寫出滿足sinx 若能對該題的結論結合圖象理解到位,熟記于心,那么相關的一些三角不等式題就迎刃而解. 例4 (1998年全國卷.6)已知點P(sinx-cosx,tanx在第一象限,則在]0,2π]內,x的取值范圍是( ). 當然該題有多種計算方法予以解答,本文解法如下: 在課堂教學改革的今天,應該怎樣進行課堂教學是我們教育工作者的首要任務.然而培養學生的創新精神不是一蹴而就的,它是一個長期的過程,在教學中必須循序漸進,長期堅持,并不斷總結經驗教訓,多與同行討論取長補短,多為我國培養創新人才. 以上是自己在教學中的點滴體會,不妥之處望批評指正.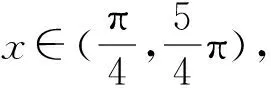
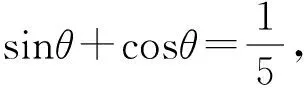
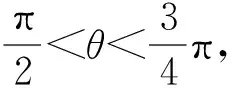
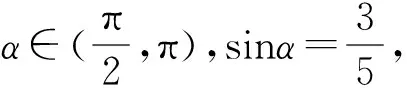
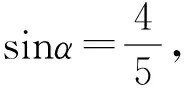
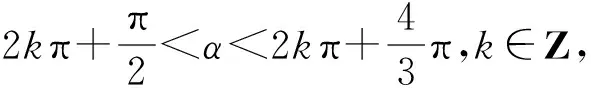
猜你喜歡
今日農業(2021年1期)2021-11-26 07:00:56
甘肅教育(2020年14期)2020-09-11 07:57:50
甘肅教育(2020年12期)2020-04-13 06:24:46
作文周刊·小學一年級版(2018年17期)2018-09-10 02:39:46
東方教育(2017年19期)2017-12-05 15:14:48
小天使·一年級語數英綜合(2017年4期)2017-04-18 17:47:11
唐山文學(2016年2期)2017-01-15 14:03:59
作文教學研究(2016年1期)2016-07-05 12:22:32
散文百家(2014年11期)2014-08-21 07:17:04
散文百家(2014年11期)2014-08-21 07:16:56

