初中數(shù)學(xué)課堂教師“追問”的策略探究

王 霞

(江蘇省如皋市搬經(jīng)鎮(zhèn)高明學(xué)校 226564)

一、在錯誤之處追問，提升學(xué)生的反思能力

學(xué)生在探索數(shù)學(xué)問題、研究數(shù)學(xué)理論時，必然會發(fā)生錯誤.在教學(xué)過程中，教師要踩準節(jié)點，展開追問，以此來引領(lǐng)學(xué)生對錯誤展開分析，進而激發(fā)學(xué)生的創(chuàng)新意識和思維，在對錯誤的剖析中獲得探索的成功.

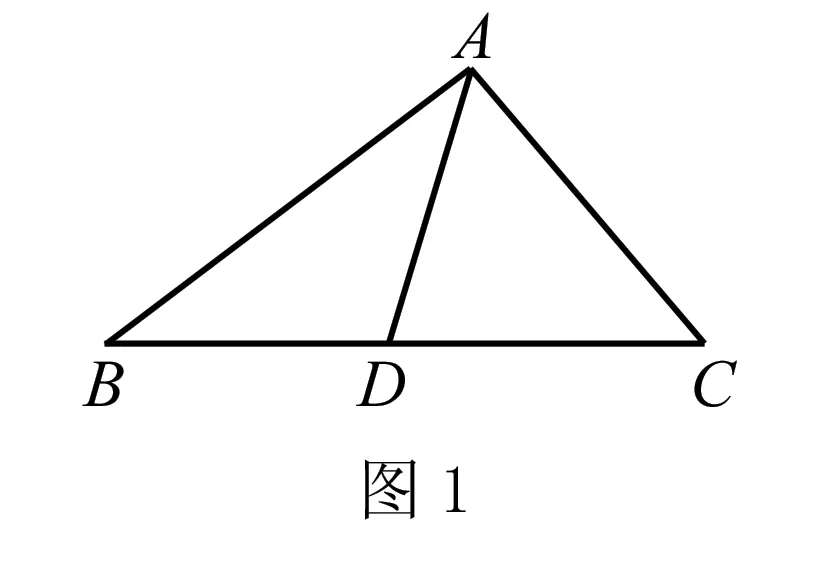
比如在引導(dǎo)學(xué)生研究三角形中線的有關(guān)性質(zhì)時，教師提供了這樣一個問題：如圖1所示的△ABC中，中線AD將其劃分成兩個小三角形，請問兩個小三角形的面積大小關(guān)系如何？很多同學(xué)在處理這個問題時，沒有經(jīng)過理性的分析，僅憑肉眼觀察大致估算圖形面積，最后得出了錯誤的答案.面對學(xué)生的錯誤，首要任務(wù)是糾錯，其次是在糾錯的基礎(chǔ)上，引領(lǐng)學(xué)生向更深層次展開研究，因此有以下一系列的追問.

師：怎樣求三角形的面積？

生：底乘以高再除以二.

師：請觀察現(xiàn)有兩個小三角形的底和高各有怎樣的特點？

生：中線AD將原有底邊分成兩個相等的部分BD和DC，如果將這兩段視為底邊，則對應(yīng)的高也是相等的，據(jù)此可確認兩個小三角形的面積相等.

師：很好，這里我們可以總結(jié)一下，有“等底等高等面積”.如果我們在另外一個底邊上構(gòu)建中線，所得到的兩個小三角形面積有何關(guān)系？

生：這兩個小三角形面積相等.

師：這兩個小三角形面積與原先的兩個小三角形面積有什么關(guān)系嗎？

生：這兩個小三角形面積與原先的兩個小三角形面積有相等的關(guān)系.

師：你們能對此進行總結(jié)嗎？

生：三角形任意一條邊上的中線將原有三角形分成兩個三角形，所得的新的兩個小三角形的面積相等，它們都等于原先三角形面積的一半.

在上述的追問過程中，教師引領(lǐng)學(xué)生對方法進行歸納，最后還通過變式問題引領(lǐng)學(xué)生進行拓展，這樣的處理可以讓學(xué)生對原有情境產(chǎn)生更加深刻的認識.

二、在粗淺處追問，讓學(xué)生探求最本質(zhì)的知識

數(shù)學(xué)的學(xué)習(xí)應(yīng)該是一個由淺入深的過程.教師的關(guān)鍵性作用在于當(dāng)學(xué)生止步于探究過程中的粗淺之處時，施以巧妙的引導(dǎo)和追問，讓學(xué)生不再停留在知識的簡單重組中，讓學(xué)生以更加靈活而深刻的思維來處理問題.

比如在指導(dǎo)學(xué)生認識整式的加減時，相關(guān)知識都比較簡單，但是教師切不可讓學(xué)生局限于那些粗淺的分析和認識，教師應(yīng)該對學(xué)生展開更深層次的追問.

師：請大家嘗試對去括號的法則進行歸納.

生：如果括號前是加號，去掉括號后，里面各項都不改變符號；如果括號前是減號，去掉括號后，里面各項都必須要改變符號.

師：如果括號前是一個數(shù)字因數(shù)，比如是3(5a+3b)，該如何處理呢？

這個問題教者提出后，要留給學(xué)生足夠的時間讓學(xué)生進行思考和小組討論，并鼓勵學(xué)生展示自己觀點.

生：如果存在數(shù)字的因數(shù)，我們首先應(yīng)該認識到這一形式的本質(zhì)其實是乘法，因此可按照乘法的分配律來去掉括號，有3(5a+3b)=15a+9b.

在上述過程中，教師果斷進行追問，以此來提出更加復(fù)雜的問題，引領(lǐng)學(xué)生獲取更好的理解.

三、在發(fā)散之處追問，提升學(xué)生思維的靈活性

初中數(shù)學(xué)為什么難？筆者認為，對初中生而言，思維的靈活性往往是他們發(fā)展數(shù)學(xué)能力的最大難點.因此在教學(xué)過程中，教師要關(guān)注學(xué)生求異思維和發(fā)展思維的發(fā)展，有效進行追問，以便讓學(xué)生以更加靈活的視角來分析和研究問題.

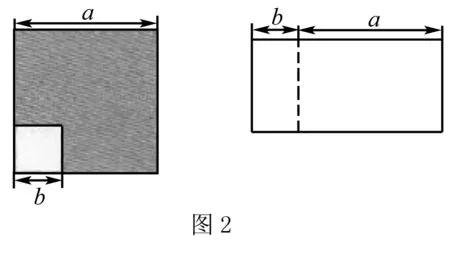
比如有這樣一個問題：如圖2所示，從一個大正方形紙片上剪下一個小正方形，兩正方形的邊長分別為a和b(a>b).(1)請用含ab的式子表示出圖中陰影部分的面積；(2)試將陰影部分拼出一個如圖2所示的長方形，你是否能求出這兩個長方形的長和寬，并寫出對應(yīng)長方形的面積?(3)結(jié)合前兩個問題的思考，你能得出平方差公式嗎？

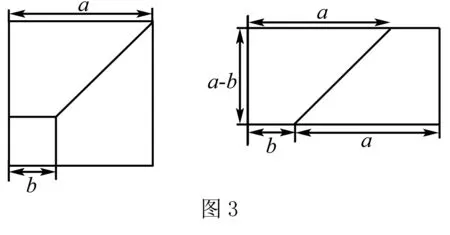
教師安排學(xué)生結(jié)合實際操作來探索，最終在觀察、比較和討論中，完成了問題的解決.學(xué)習(xí)并沒有在此結(jié)束，追問即將開始.

師：請思考，是否還有其他的拼法來完成平方差公式的驗證？

生1：我可以采用如圖3所示的方法來拼湊和驗證.

生2：我還可以拼成一個平行四邊形，可以…….

生3：我能夠拼出一個梯形，可以…….

……

進一步的追問激起了學(xué)生的思維，學(xué)生采用多樣化的手段促成了問題的解決，對他們本身也是一種鼓勵.

作為一名初中數(shù)學(xué)教師應(yīng)該在實踐中時刻強化“追問”策略的積累，這不僅能提升教師思維能力，也有助于教師自身發(fā)展能力的提高.