弧形濾毒罐氣動特性3D數值模擬研究

司芳芳，葉平偉,2，皇甫喜樂，王泠沄，楊德瑞

(1.防化研究院， 北京 100191； 2.國民核生化災害防護國家重點實驗室， 北京 102205)

防毒面具濾毒罐是呼吸道個人防護裝備中最核心的部件之一。濾毒罐主要由濾煙層(過濾層)、吸附層(吸收層)組成，以確保對灰塵、氣溶膠的過濾和毒劑的吸收。

西方國家在濾毒罐產品的研制和生產方面主要由3M、AVON、BACOU和North等幾家大公司壟斷。英國AVON protection公司在軍用防毒面具和濾毒罐開發中占有重要的地位，由其開發的濾毒罐系列產品在國際上具有代表性，在美國、英國和北約其它國家得到了大量的應用。

因為傳統圓柱形濾毒罐結構(非異形結構)重心偏下移，離面部較遠，扭矩偏大，劇烈運動時由于濾毒罐的擺動易造成防毒面具漏氣；此外，呼吸阻力過大，生理負荷較重。因此，從2000年開始，英國AVON protection公司歷時5年成功開發出了FM50系列(含FM50、FM52、FM53)濾毒罐。其中FM50是為美軍研制的JSGPM濾毒罐，該型濾毒罐采取異性結構，罐蓋設計有導流槽，使得氣流分布更均勻。FM53面具濾毒罐采用弧形結構，濾毒罐和面罩能更有效的貼合，從而在一定程度上提高了面具佩戴的動氣密性，且濾毒罐采用弧形設計，有效提高了過濾面積，降低了通氣阻力。

開發高效、低阻力的新型防毒面具濾毒罐，可以通過以下兩方面來進行：一是提升裝填材料的濾毒性能；二是優化濾毒罐內部結構。優化濾毒罐結構必須考慮濾毒罐空氣動力學特性，包括通氣阻力和流場結構。

隨著計算機和數值計算方法的快速發展，計算流體動力學 (CFD) 方法可以克服傳統實驗方法無法觀察多孔介質內氣流場分布的難點[1～4]，通過數值模擬來確定吸附層和濾煙層內流場結構。Yin Chia Su和Chun Chi Li等采用CFD方法對濾毒罐進行3D數值模擬，他們主要研究了62A濾毒罐上網板和下網板上開孔方式、吸附層厚度對濾毒罐通氣阻力和死區范圍的影響[5～7]。

目前國內常用濾毒罐仍為傳統的圓柱形結構，為了在不降低防護能力基礎上減小濾毒罐的通氣阻力，提高使用人員的舒適性和安全性，本文采用CFD數值分析方法，參考FM53弧形濾毒罐結構，研究了多種弧形濾毒罐結構形式，數值模擬分析其內部氣動特性，重點研究吸附層氣流分布情況；并研究了導流槽結構對濾毒罐氣動特性影響，從理論上深入剖析，為濾毒罐結構優化提供了理論依據。

1 弧形罐結構

目前國內常用的濾毒罐結構如圖1所示。本文研究濾毒罐模型的殼體參考M53面具弧形罐的殼體弧度，通過改變上網板弧度，設計研究了三種濾毒罐結構形式，如圖2、圖3、圖4所示。

圖1 通用的濾毒罐(模型A)

圖2 單面弧結構濾毒罐(模型B)

圖3 雙面弧結構濾毒罐(模型C)

圖4 導流槽結構濾毒罐(模型D)

模型B炭層進氣一端為平面結構，出氣口(與面罩相連接的一端)為弧形結構；模型C炭層兩端均為弧形；模型D無下網板，出氣口附近殼體為導流槽結構。對比圓柱形濾毒罐和弧形濾毒罐可以看出，弧形濾毒罐和面罩能更有效貼合，從而在一定程度上提高了面具佩戴的動氣密性；雙面弧結構濾毒罐吸附層是弧形設計，能有效提高過濾面積。

同時設計了兩種網板開孔方式，如圖5所示，其中圖5(a)與目前通用的某型號罐模型A(圖1)的網板開孔方式一致，該網板定義為a網板，另一個定義為b網板。具體模型參見表1。

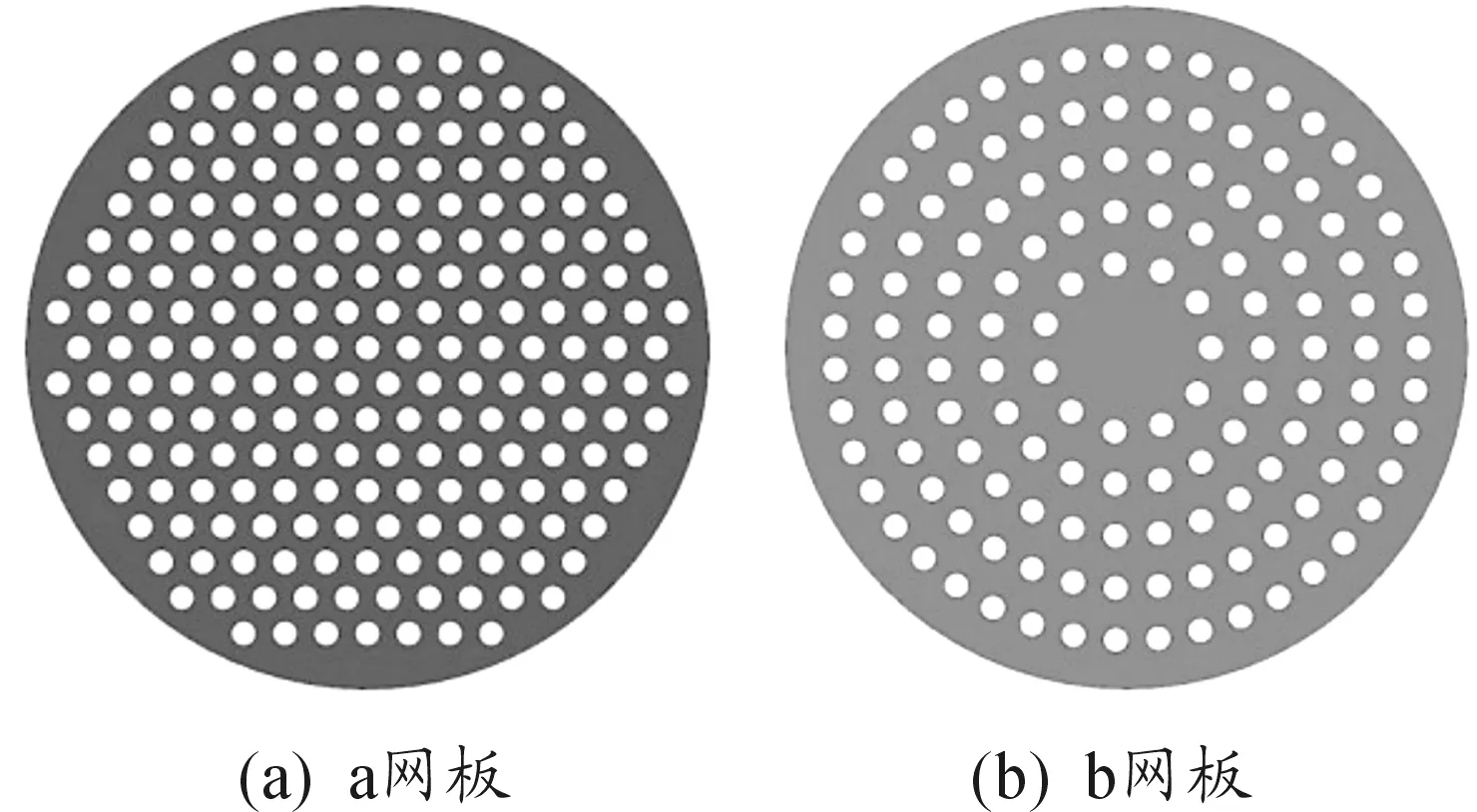
圖5 網板開孔示意圖

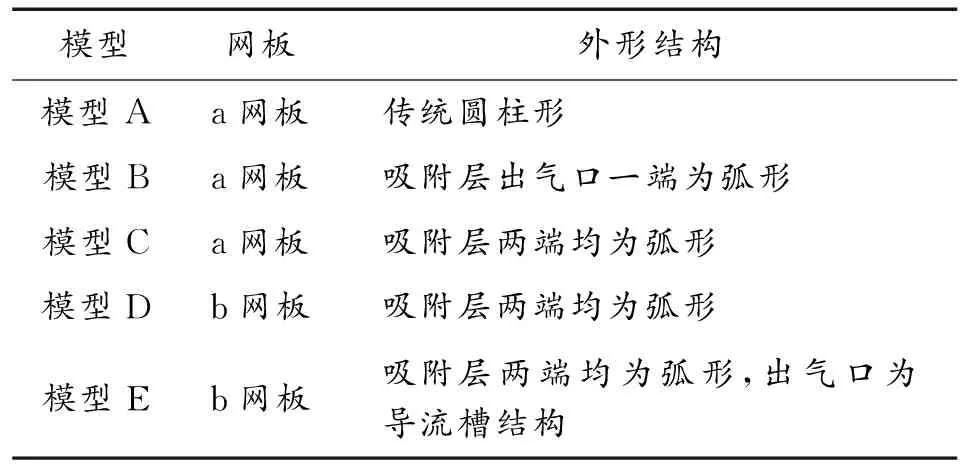
模型網板外形結構模型Aa網板傳統圓柱形模型Ba網板吸附層出氣口一端為弧形模型Ca網板吸附層兩端均為弧形模型Db網板吸附層兩端均為弧形模型Eb網板吸附層兩端均為弧形,出氣口為導流槽結構

2 數值模擬方法

2.1 控制方程

控制方程采用三維雷諾平均納維-斯托克斯(Navier-Stokes)方程。本文引入滯留時間來確定濾毒罐防護能力的保持情況。滯留時間是指：空間中某一點，空氣在空間內已停留的時間，滯留時間越大表明空氣停留時間越長。滯留時間指數取代吸附時間的優點是復雜的瞬態吸附模式不再求解，大大縮短了計算時間。滯留時間方程[3]是：

(1)

式(1)中，ρ是氣體密度；τ是當地平均滯留時間；μeff/στ是湍流模型中的當地實際擴散系數；μeff=μl+μt(μeff是有效粘度、μl是分子粘度，μt是紊動粘度)；στ= 1。

本文所有模擬中濾毒罐入口氣流流量是恒定的，因此入口邊界定義為速度入口。在入口處，參考壓力值為 101 325 Pa。出口邊界條件是壓力出口邊界。壁面為無滑移邊界。

本研究使用 FLUENT 求解器。對流項離散采用二階迎風格式，粘性項離散采用二階中心差分格式。壓力-速度耦合采用COUPLE算法。

為了簡化計算，本文研究省略多褶濾紙的影響，把過濾層視為單一層，且假定兩個多孔介質層為各向均勻的。由于所有模型都是左右對稱的，所以僅模擬1/2結構。對于異形結構濾煙層而言，弧形狀濾煙層折疊過程中容易造成過濾紙的損壞，降低過濾效率，故實驗仍采用平面結構濾煙層，因此計算中濾煙層也采用平面結構。本文重點研究濾毒罐弧形結構對吸附層氣動特性影響，因此所有模型濾紙高度和褶數一樣。所有模型的數值模擬均采用非結構網格。由于5個模型的網格結構類似，本文僅給出模型A和模型C的網格示意圖，如圖6、圖7所示。

圖6 模型A網格圖7 模型C網格

2.2 多孔介質參數

濾毒罐的通氣阻力主要來自濾紙和活性炭，濾紙和活性炭都是多孔介質。達西首先推導出描述流體流經多孔介質 的動量耗散方程，即達西方程：

(2)

式(2)中，ΔP是多孔介質區域的通氣阻力；L是流經方向的長度；κ是滲透率；μ是流體粘度，Vs表示進入多孔介質區流體的表面速度。達西方程只考慮粘度的影響，當雷諾數增加時，必須增加對流項以考慮慣性效應，這就產生了Forchheimer方程。 Forchheimer方程描述了在多孔介質區域的通氣阻力和表面速度之間的關系。

(3)

式(3)中，α是多孔材料或粘度參數的滲透率倒數；β通常稱為慣性參數。 當Vs很低或雷諾數很小時，慣性效應遠遠小于粘效應。隨著雷諾數的增加，多孔介質的流動特性逐漸從線性 (Darcy方程) 變為非線性(Forchheimer方程)，該流動行為包括從層流到湍流流動的瞬時變化[6]。

通過實驗測得玻纖濾紙和活性炭不同入流流量下的通氣阻力，利用曲線擬合獲取濾煙層及吸附層Forchheimer方程中的參數。 濾煙層的多項式是：

(4)

吸附層的多項式是：

(5)

濾煙層系數為：

α1=2.19×109m-2，β1=7.5×104m-1

吸附層系數為：

α2=2.03×109m-2，β2=7.5×104m-1

3 結果分析

3.1 外形結構影響

首先數值模擬了無濾紙和活性炭的空罐，入口氣流流量為 30 L/min。圖8、圖9給出了模型A、模型B和模型C對稱截面上速度矢量分布圖。

圖8 模型A(空罐)吸附層x=0截面處速度矢量

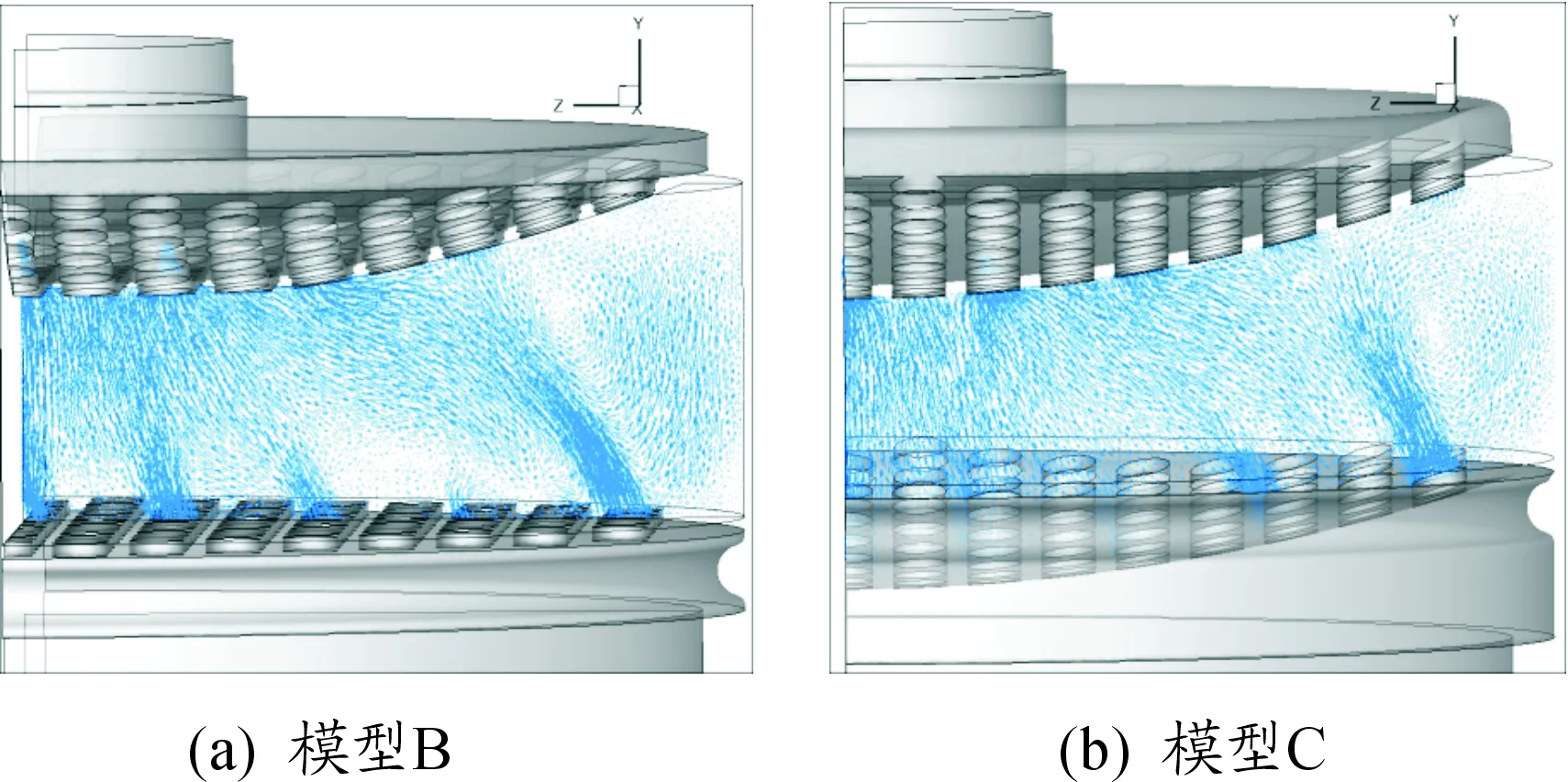
圖9 空罐吸附層x=0截面處速度矢量

從圖8、圖9中可以看出，吸附層最外側都有回流區。當流體流經吸附層時，多孔流不會造成周邊區域的回流。但是，如果流體不易流入該區域，容易形成死區，減少了流動區域，進而增加了流經區域的表面速度和通氣阻力。

考察了入流流量Q=15、20、30、45、60、85、110 L/min時，模型A、模型B和模型C僅吸附層、僅濾煙層和包含濾煙層和吸附層兩種多孔介質的通氣阻力，如圖10所示。

圖10 不同Q時模型A、B、C通氣阻力比較

對比模型A數值模擬與實驗結果可以看出，相差不到3%，表明本文采用的數值方法模擬精度較高。從圖10中可以看出，隨著流量增加，濾毒罐通氣阻力增加；Q≤30 L/min時，吸附層與濾煙層通氣阻力相差很小，隨著Q增大，吸附層通氣阻力與濾煙層通氣阻力差值越來越大。

為了具體分析三個模型對濾毒罐氣動特性的影響，重點研究了Q=30 L/min時數值模擬結果。模型C的通氣阻力為108 Pa，相比模型A減小4.6%，相比模型B減小2.7%，由此可見，弧形結構能減小濾毒罐通氣阻力，且雙弧形罐的通氣阻力最小。圖11給出了吸附層對稱截面上氣流停滯時間等值線分布。

圖11 吸附層對稱截面上氣流停滯時間等值線(UDS0代表停滯時間；Q=30 L/min)

從圖11可以看出，模型B在吸附層外側出口附近大片區域氣體停留時間較長，在中間區域停留時間較短，氣流停留時間不均勻，而模型A和模型C的氣流停留時間相對均勻，僅在吸附層外側出氣口區域停留時間相對較長。結合圖12、圖13可以看出，模型A和C的氣流滯留時間在活性炭外側1/5區域開始明顯增加，而模型B在吸附層外側2/5區域開始明顯增加；氣流滯留時間短表明氣流通過該區域的速度值高，而氣流滯留時間長表明氣流通過該區域的速度值低；局部高速流快速通過出口，導致氣體不易流經外側區域，會增加死區范圍，且造成高速區吸附不充分，進而降低整個炭層的利用效率。模型A和模型C的滯留時間曲線分布趨勢類似，但模型C氣流在炭層停留時間較長，速度較小，這表明雙弧形濾毒罐吸附層能提高氣流的接觸面積，整體氣流流速變慢，氣體與吸附層的接觸時間變長，炭層的利用率有一定程度的提高。

圖12 吸附層x=0截面上不同吸附層高度氣流滯留時間分布(h代表活性炭高度；Q=30 L/min)

3.2 導流槽影響

主要考察了入流流量Q=15、20、30、45、60 L/min時模型D、E的通氣阻力，通過對比Q=30 L/min時模型D與模型E吸附層氣流滯留時間和速度，研究去掉下網板，出氣口殼體改為導流槽結構對濾毒罐氣動特性影響。

首先研究了模型D和模型E在不裝填濾紙和活性炭時內部流場分布，重點研究了吸附層氣流分布。圖14給出了模型D、模型E對稱截面上速度矢量分布圖。

從圖14可以看出，模型D吸附層最外側有回流區，而模型E在吸附層中間部分有大的回流區。圖15給出了模型D、E裝填濾紙和活性炭時通氣阻力隨氣流流量變化。

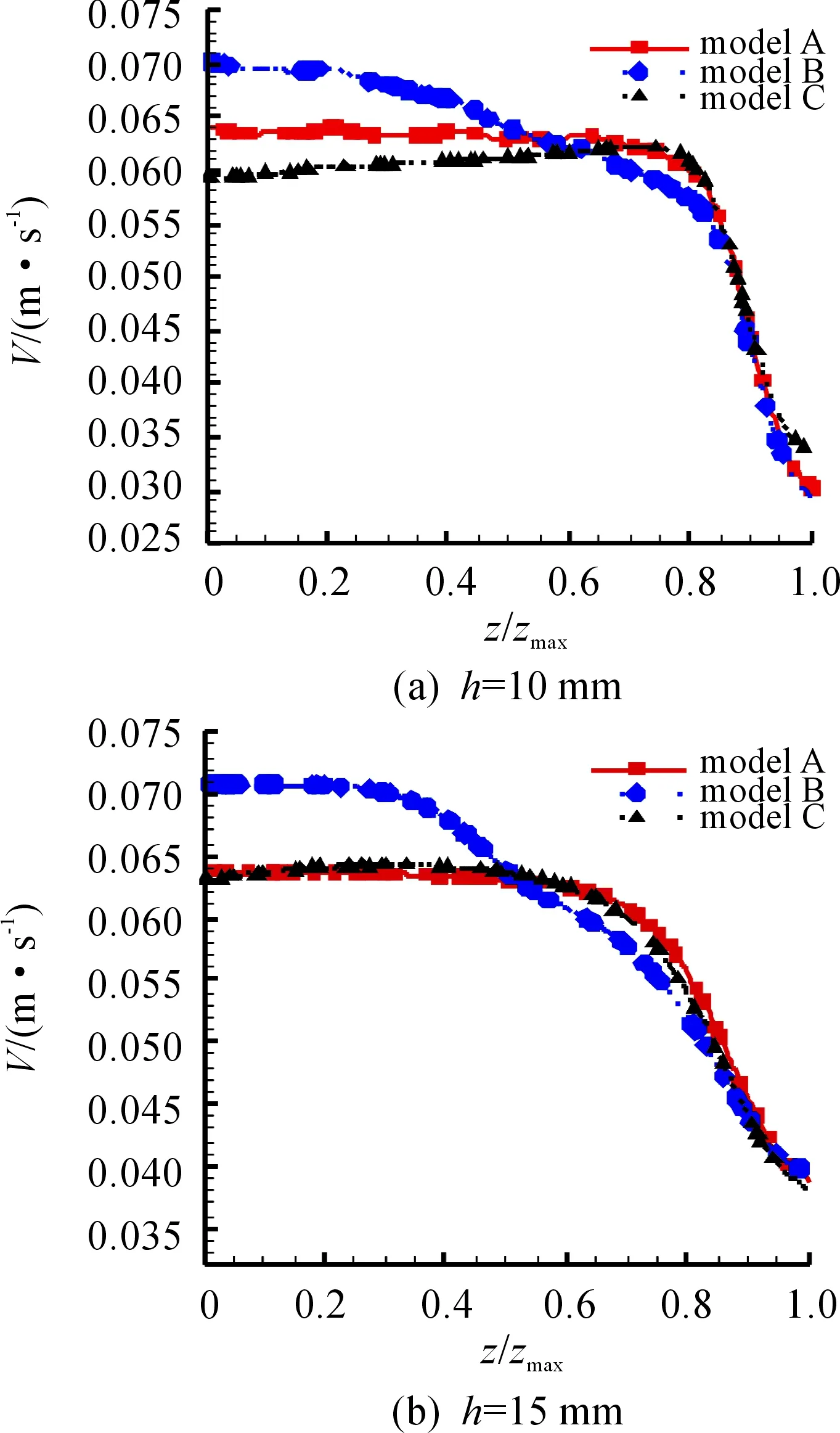
圖13 吸附層x=0截面上不同吸附層高度氣流速度分布(Q=30 L/min)

圖14 空罐吸附層x=0截面處速度矢量

從圖15可以看出，模型D的通氣阻力略大于模型E的通氣阻力，隨著氣流增大，二者差值增大，Q=30L/min時相差約2.4%。這表明導流槽結構可以減小濾毒罐通氣阻力。

模型D和模型E吸附層對稱截面上氣流停滯時間等值線分布圖和不同吸附層高度滯留時間分布圖如圖16、17所示。

圖15 不同Q時模型D、E通氣阻力

圖16 吸附層對稱截面上氣流停滯時間等值線(UDS0代表停滯時間，單位s)

圖17 吸附層x=0截面上不同吸附層高度氣流滯留時間分布曲線

從圖16、圖17可以看出，模型D氣流在整個吸附層滯留時間比模型E長，且二者差距較大。模型D在吸附層外側近下網板附近區域氣體停留時間相對較長，其他區域氣流滯留時間相對均勻；而模型E氣流滯留時間分布不均勻，在吸附層內側1/5區域和外側1/5區域停留時間相對較長。吸附層不同高度氣流速度分布如圖18所示。

從圖18可以看出，在活性炭層高度為5 mm處，模型D和模型E在外側3/10區域氣流速度基本一致，而在內側區域模型E速度較大；隨著活性炭層高度增加，模型D與模型E在外側3/10區域氣流速度仍基本一致，而在內側區域氣流速度差值增大。這表明下網板對氣流產生一定的阻力，使中間區域氣流流速變慢，氣體與吸附層的接觸時間變長，而導流槽結構不能抑制中間高速氣流，使得氣體快速通過吸附層，有可能會造成毒劑吸附不充分，但導流槽結構明顯減小吸附層外側區域氣體停留時間。

圖18 吸附層x=0截面上不同吸附層高度氣流速度分布曲線

4 結論

本文采用CFD 方法研究了五種濾毒罐(一種圓柱形濾毒罐和四種弧形濾毒罐)的氣動特性，主要考察了弧形罐結構和導流槽結構對濾毒罐空氣動力學特性的影響。

數值模擬結果表明網板開孔大小、數量和位置相同時，雙弧形濾毒罐吸附層能提高氣流的接觸面積，整體氣流流速變慢，氣體與吸附層的接觸時間變長，活性炭的利用率有一定程度的提高，且通氣阻力相比目前通用的濾毒罐和單弧形罐小。導流槽結構可以減小濾毒罐通氣阻力，但不能抑制吸附層中間高速氣流，使得氣體快速通過吸附層。因此，我們將進一步研究弧形的弧度對濾毒罐氣動特性影響，優化濾毒罐結構，達到既降低濾毒罐通氣阻力，又能提高炭層利用效率的目的。