基于干擾觀測器的永磁同步電動機滑模控制

顏漸德，王 輝 ，蘭永紅，羅勝華

(1.湖南大學,長沙 410082; 2.湖南工程學院,湘潭 411101;3.湘潭大學,湘潭 411105; 4.湖南電氣職業技術學院,湘潭 411101)

0 引 言

永磁同步電動機(以下簡稱PMSM)因其具有能量密度高、效率高、可靠性高等優點，在交流驅動系統中得到廣泛的應用。然而，PMSM是典型的多變量和強耦合的非線性系統、存在參數攝動、外部干擾等不確定因素，導致PMSM控制系統的動態性能下降。如何尋求有效的控制策略，克服PMSM系統的外部干擾以提高系統的性能，引起了國內外學者的廣泛關注[1]。

近年來，許多學者在提高PMSM的速度跟蹤性能上，提出了許多控制策略，如：矢量控制[2]、反推控制[3-4]、自適應控制及無源控制等[5-7]。文獻[4,8]針對PMSM矢量控制系統，通過構造新的子系統，并選取合適的虛擬變量和虛擬控制函數，利用李雅普諾夫穩定性理論設計控制量，從而使系統具有全局穩定性，實現良好的系統跟蹤。滑模變結構控制算法簡單、魯棒性好和可靠性高，對提高動態特性效果明顯[9-11]。文獻[12]設計了一種積分時變滑模變結構的速度環控制器，解決了傳統PID控制器魯棒性差、系統抗擾能力弱和動態響應性能不佳的問題。文獻[13]對PMSM的無速度傳感器控制進行研究，對滑模速度觀測器進行了改進。為了減小延時并提高伺服系統電流環控制性能，文獻[14]提出了一種基于無差拍控制原理的PMSM魯棒預測電流控制算法。文獻[15]為了增強系統的抗干擾性，提出了一種用于表面式PMSM的上下界滑模變結構速度控制方法。文獻[16]提出一種擾動補償控制方法。總之，以上方法具有較高的跟蹤精度和魯棒性，由于設計過程中沒有對外部干擾進行估計，系統中參數微小變化或存在外部干擾時，系統的速度會存在一個較大的過沖，從而使得系統跟蹤性能下降。

受以上文獻啟發，本文提出一種基于干擾觀測器和滑模控制器相結合的PMSM速度控制方法。設計基于指數趨近律的滑模控制器，以提高電機系統的靜態和動態跟蹤性能。為了補償負載干擾，進一步設計基于干擾觀測器(以下簡稱DOB)的反饋控制特性。仿真與實驗表明，本文的方法提高了PMSM控制系統速度跟蹤精度，對負載干擾具有較好的抑制效果。

1 PMSM的數學模型及問題描述

為了簡化分析，首先做如下假設：氣隙中轉子永磁磁場為正弦波；定子鐵心不飽和，忽略渦流和磁滯損耗；轉子上無阻尼繞組。在以上假設下，得到PMSM在d,q坐標系下的數學模型，其電壓方程[3]：

(1)

式中：Ld,Lq分別為交、直軸電感；Rs為PMSM的定子電阻；ω為PMSM的角速度；ψf為交鏈磁鏈；uq,iq為PMSMq軸上的電壓與電流分量；ud,id為PMSMd軸上的電壓與電流分量。

PMSM的轉矩方程：

(2)

式中：Te為PMSM的轉矩；p為PMSM的極對數。對于隱極式PMSM,有Ld=Lq，因此可將PMSM的轉矩方程簡化：

(3)

PMSM的運動方程[3]：

(4)

式中：J,B分別為系統的轉動慣量和摩擦系數；TL為系統的負載轉矩。

將式(4)代入式(3)，可得：

(5)

式中：J=J0+ΔJ，TL=TL0+ΔTL，J0和TL0是系統參數的確定值，ΔJ和ΔTL表示系統參數的不確定性。

考慮到電機參數變化及未建模不確定性，式(5)可以進一步表示：

(6)

式中：Δa，Δb，Δc為系統參數不確定性攝動。

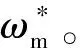
(7)

式中：d為不確定性干擾。

PMSM系統要求輸出速度響應快、運行平穩，具有較高的速度跟蹤精度。然而實際運用中，沒有考慮外界干擾(如式(7)中的d)，會導致系統速度跟蹤精度下降，從而影響PMSM控制系統性能。為了保證系統具有良好的穩定性和魯棒性。本文提出一種基于DOB的滑模控制器，以提高PMSM控制系統的跟蹤精度及外部干擾抑制能力。其控制系統結構框圖如圖1所示，圖1中，ω*為給定轉速，e為速度誤差，SMC為滑模控制器。

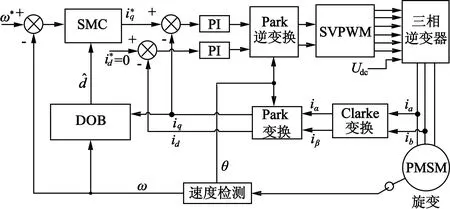
圖1 基于DOB與SMC的結構框圖

2 控制系統設計

2.1 滑模控制器設計

針對標稱系統式(7)，即d=0，定義滑模面：

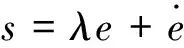
(8)

式中：λ為正常數。

對式(8)求導，可得：

(9)

趨近律函數采用指數趨近律：

(10)

式中：sat(·)為削弱抖振的飽和函數：

(11)

選取李雅普諾夫函數：

(12)

為抑制不確定的干擾，將DOB觀測到的干擾估計引入控制器，由式(9)和式(10)，基于干擾補償的滑模變結構控制律,q軸參考電流可設計：

(13)

對V2關于時間求導，根據式(9)有：

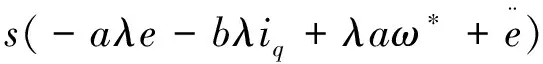
(14)

(15)

根據李雅普諾夫穩定性，閉環系統漸近穩定。因此在有限時間內，位置跟蹤誤差都將達到邊界層。由式(8)和式(11)可知，速度跟蹤誤差的邊界可以限定：

2.2 DOB的設計

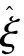
常見的DOB結構框圖如圖2所示。

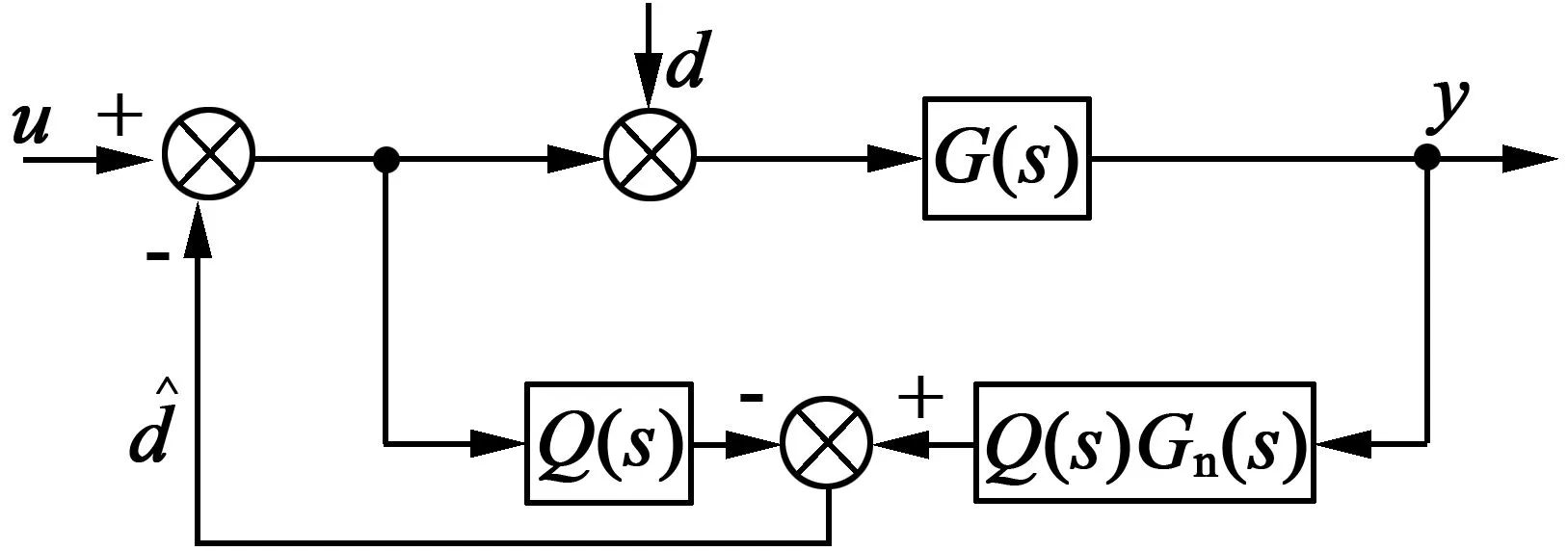
圖2 DOB結構控制框圖

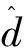
(16)

另外，由圖2可以得出如下輸入輸出關系：

y=Gny(s)u+Gdy(s)D(s)

(17)

式中：

(18)

(19)

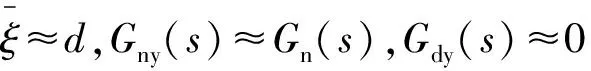
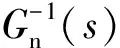
3 仿真與實驗結果

3.1 仿真結果

為驗證PMSM控制系統中，基于DOB的滑模控制器(DOB-SMC)的有效性，應用MATLAB/Simulink軟件進行了仿真。PMSM的主要參數如表1所示；控制系統其他參數：摩擦系數B=0.008 N·m·s/rad，轉動慣量J=0.000 35 kg·m2；控制器參數設置：λ=2 000，k=150，ε=500。

表1 永磁同步電動機參數

上述PMSM系統簡化后得到速度環名義模型傳遞函數[17]：

(20)

為滿足DOB設計條件，本文采用3階低通濾波器[18]：

(21)

式中：τ為時間常數，決定Q(s)的截止頻率。

初始給定轉速為1 200 r/min，在0.6 s時給定速度為1 000 r/min，在0.8 s，加入了一個負載干擾。圖3給出了SMC與DOB-SMC的速度響應波形。實線和虛線分別為采用SMC與DOB-SMC的速度跟蹤曲線，由圖3可以看出，SMC與DOB-SMC電機的轉速跟蹤性能良好，但當有負載或干擾時，DOB-SMC比SMC更快地達到穩定，且過沖更小。因此，DOB-SMC的干擾抑制效果明顯。

圖4為SMC與DOB-SMC的電磁轉矩響應波形。圖5,圖6分別為SMC與DOB-SMC的三相電流波形。當速度瞬間變化時，三相電流會有尖峰，對應的轉矩與電流成正比。

圖3 SMC與DOB-SMC的速度響應

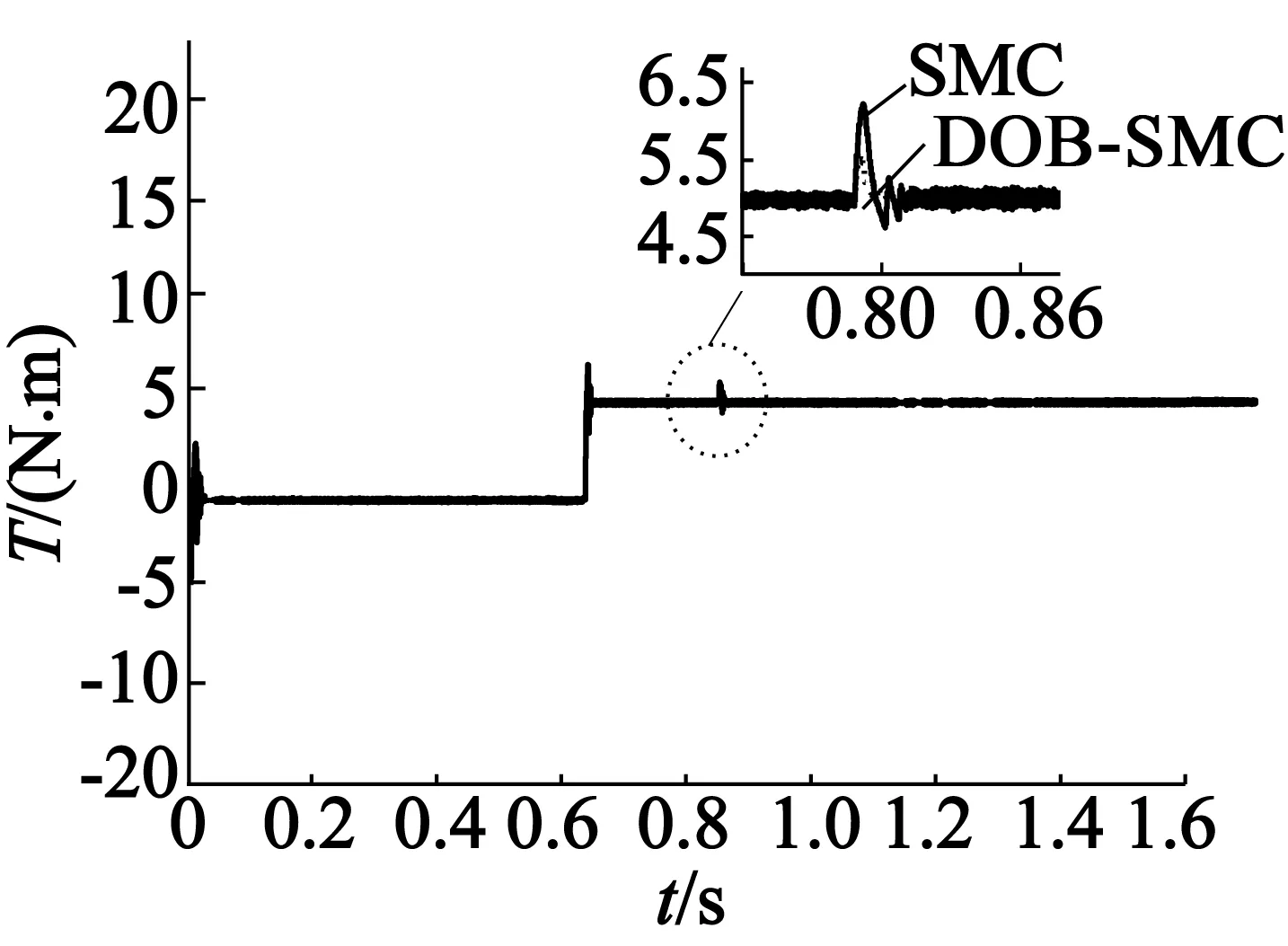
圖4 SMC與DOB-SMC的電磁轉矩響應

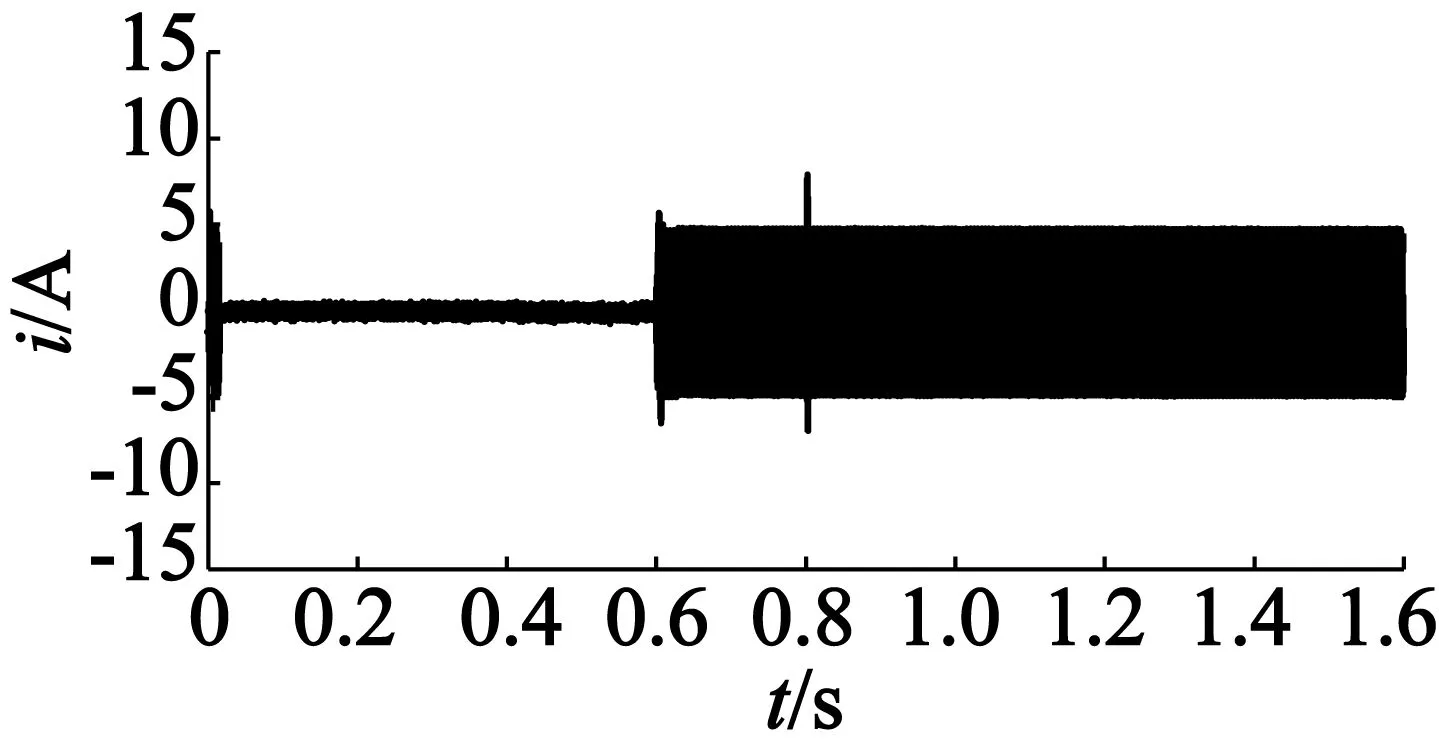
圖5 SMC的三相電流波形

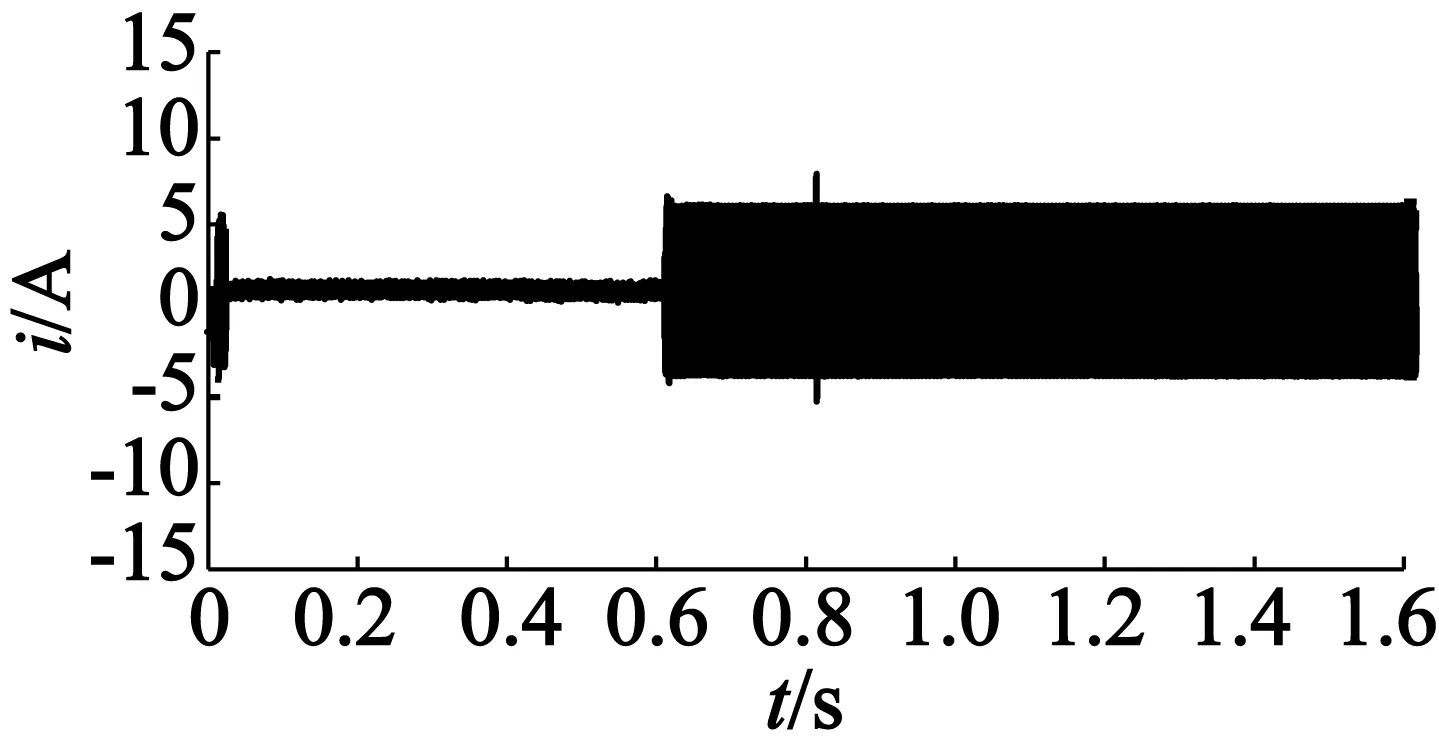
圖6 DOB-SMC的三相電流波形

綜上所述，本文的速度跟蹤控制方法，能及時跟蹤電磁轉矩和給定的轉速，使系統具有響應快，超調小，抑制負載干擾強等優點。

3.2 實驗結果

PMSM實驗平臺如圖7所示，平臺中有2臺PMSM，其中1臺PMSM工作在電動狀態，另1臺PMSM工作在發電狀態來模擬負載，負載大小由上位機軟件調節，電機參數如表1所示。采用TI公司的DSP處理器TMS320F28035，功率器件采用英飛凌智能模塊IPM。需要觀測的數據可以通過軟件設置在DSP主控板的模擬輸出。

圖7 永磁同步電動機實驗平臺

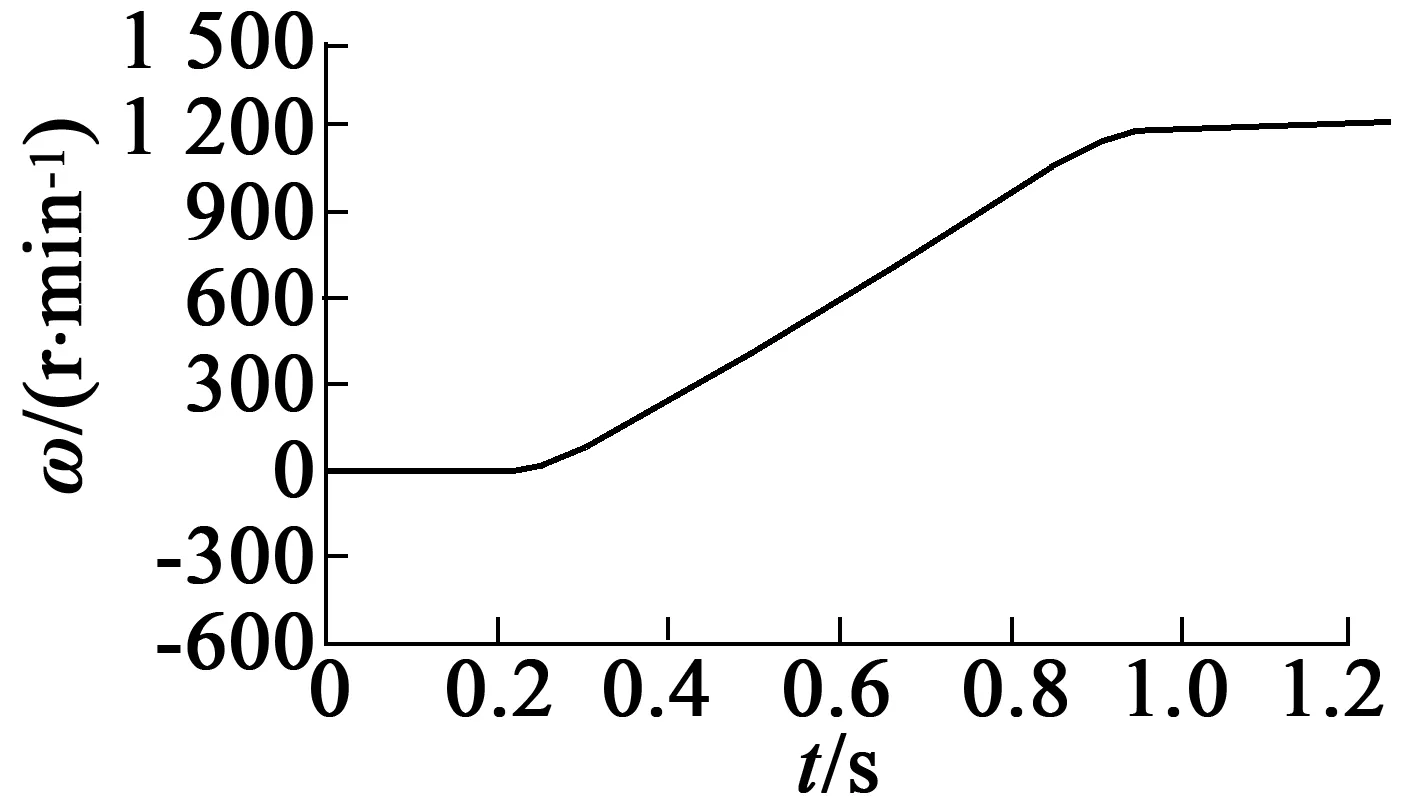
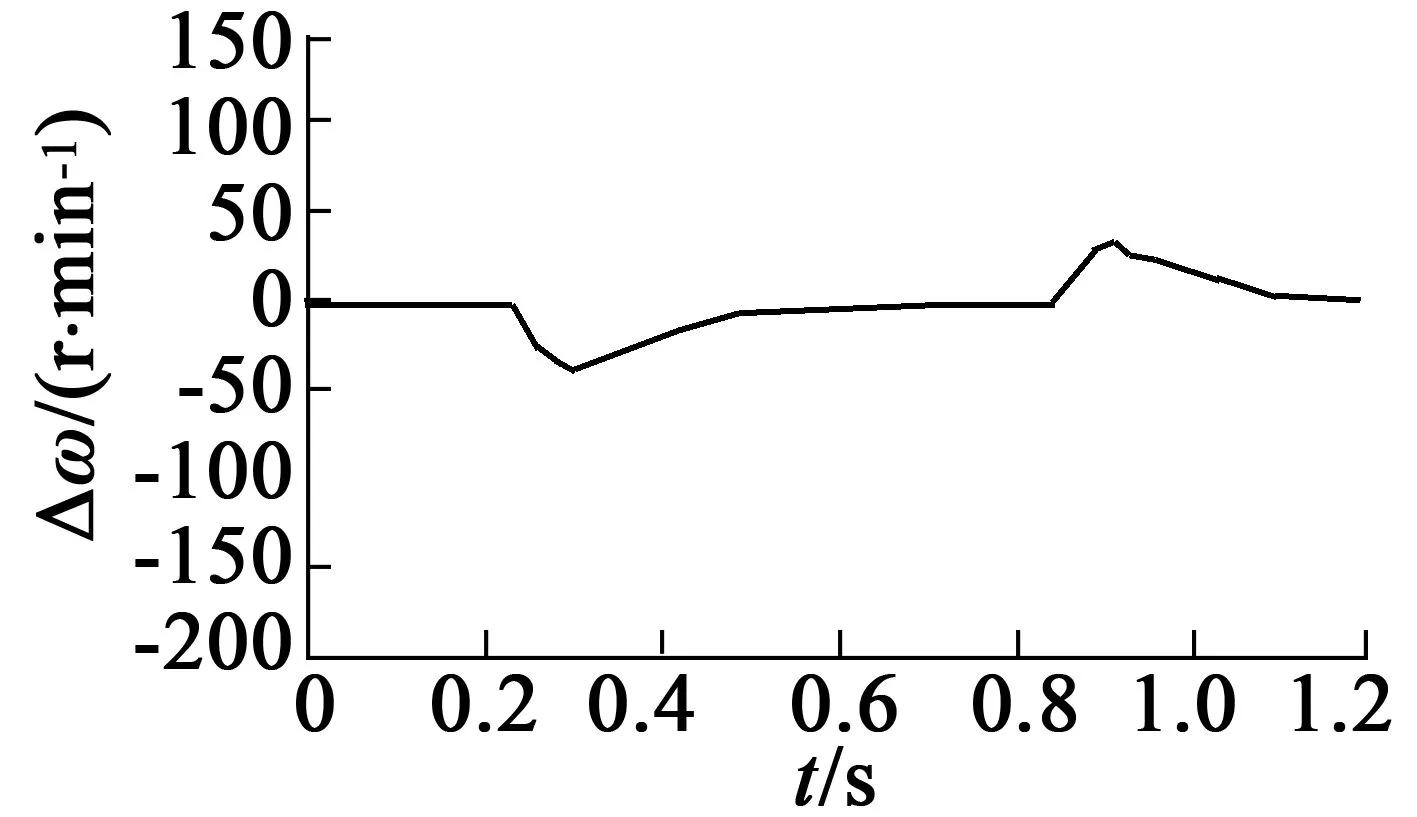
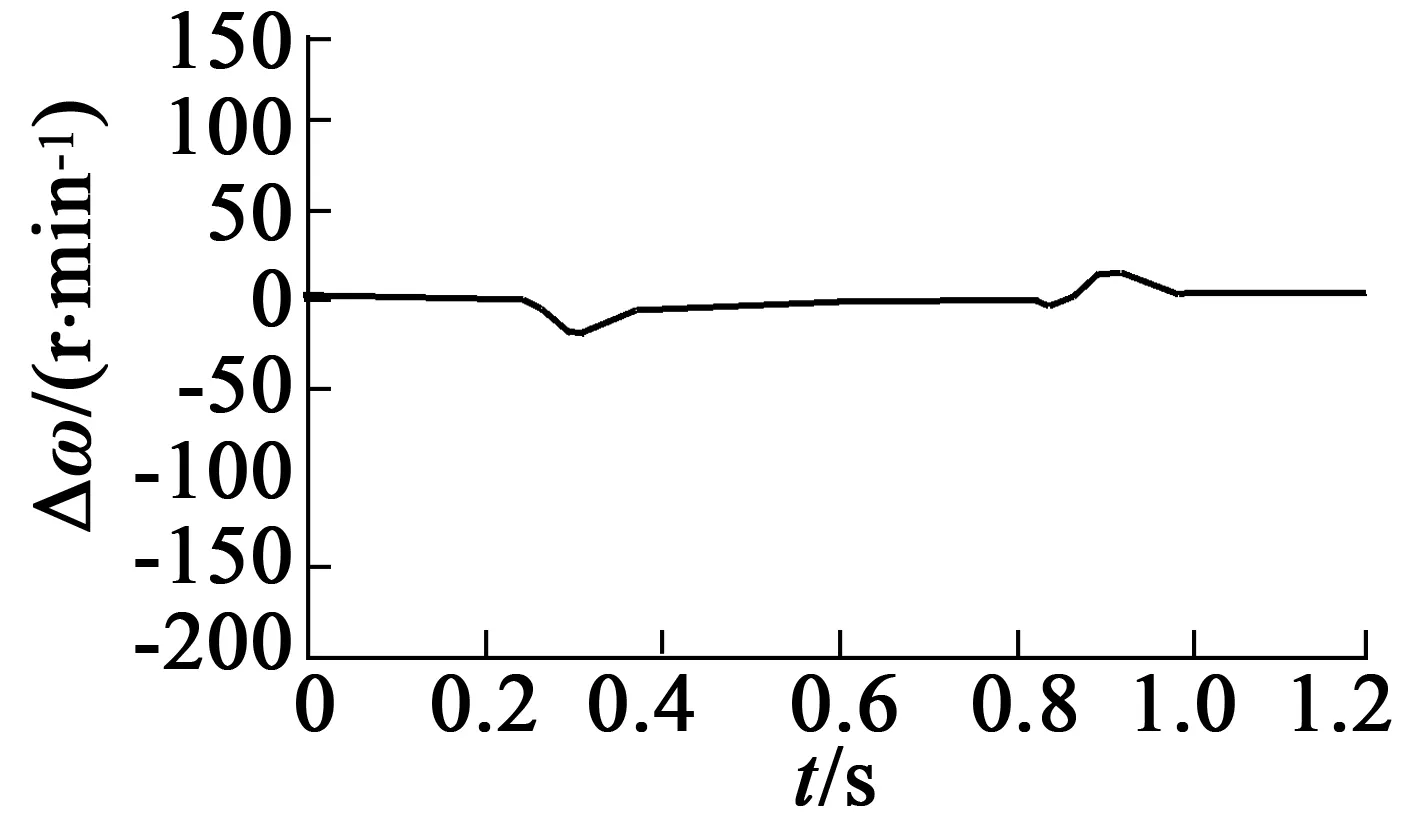
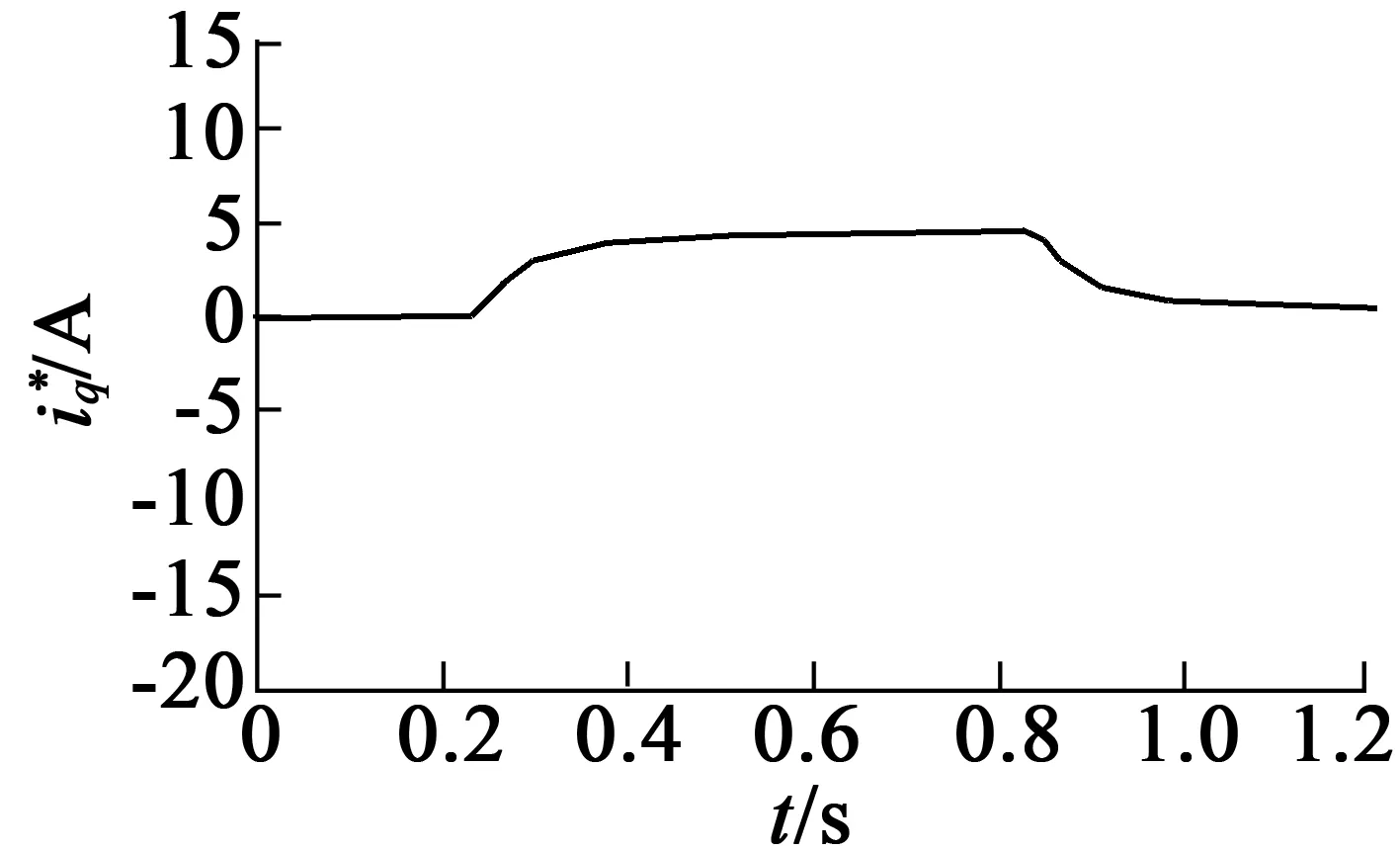
電機初始速度為0，從0.25 s開始均勻增速，到0.9 s時速度達到1 200 r/min，負載為0。圖8、圖9分別為SMC和DOB-SMC的實驗波形。由圖8的速度跟蹤誤差曲線可以看出，傳統SMC的速度跟蹤誤差從0.25～0.5 s時間內速度存在誤差，速度誤差幅度最大達到40 r/min。由圖9的DOB-SMC速度跟蹤誤差曲線可以看出，從0.2～0.35 s時間內速度也存在誤差，速度誤差幅度最大達到20 r/min。圖10(b)中DOB-SMC的q軸參考電流波形，明顯比圖10(a)中傳統SMC的電流波形平滑。

(a) SMC

(b) DOB-SMC

(a) SMC

(b) DOB-SMC

(a) SMC

(b) DOB-SMC

電機初始速度為1 000 r/min，負載為5 N·m，在0.25 s時將負載轉矩增加至10 N·m，傳統SMC與DOB-SMC速度響應與控制器輸出的q軸參考電流分別如圖11、圖12所示。圖11(a)中，在0.25 s時，負載轉矩增加到10 N·m時，傳統SMC速度最低為860 r/min，在0.48 s時達到穩定，調節時間為0.23 s;圖12(a)為傳統SMC輸出的q軸參考電流，最大為5 A。由圖11(b)為基于DOB-SMC速度最低為880 r/min，在0.35 s時達到穩定，調節時間為0.1 s，圖12(b)為基于DOB-SMC輸出的q軸參考電流，最大為4.8 A。由此可得出，本文的方法控制效果明顯，具有較高的跟蹤精度和響應速度。

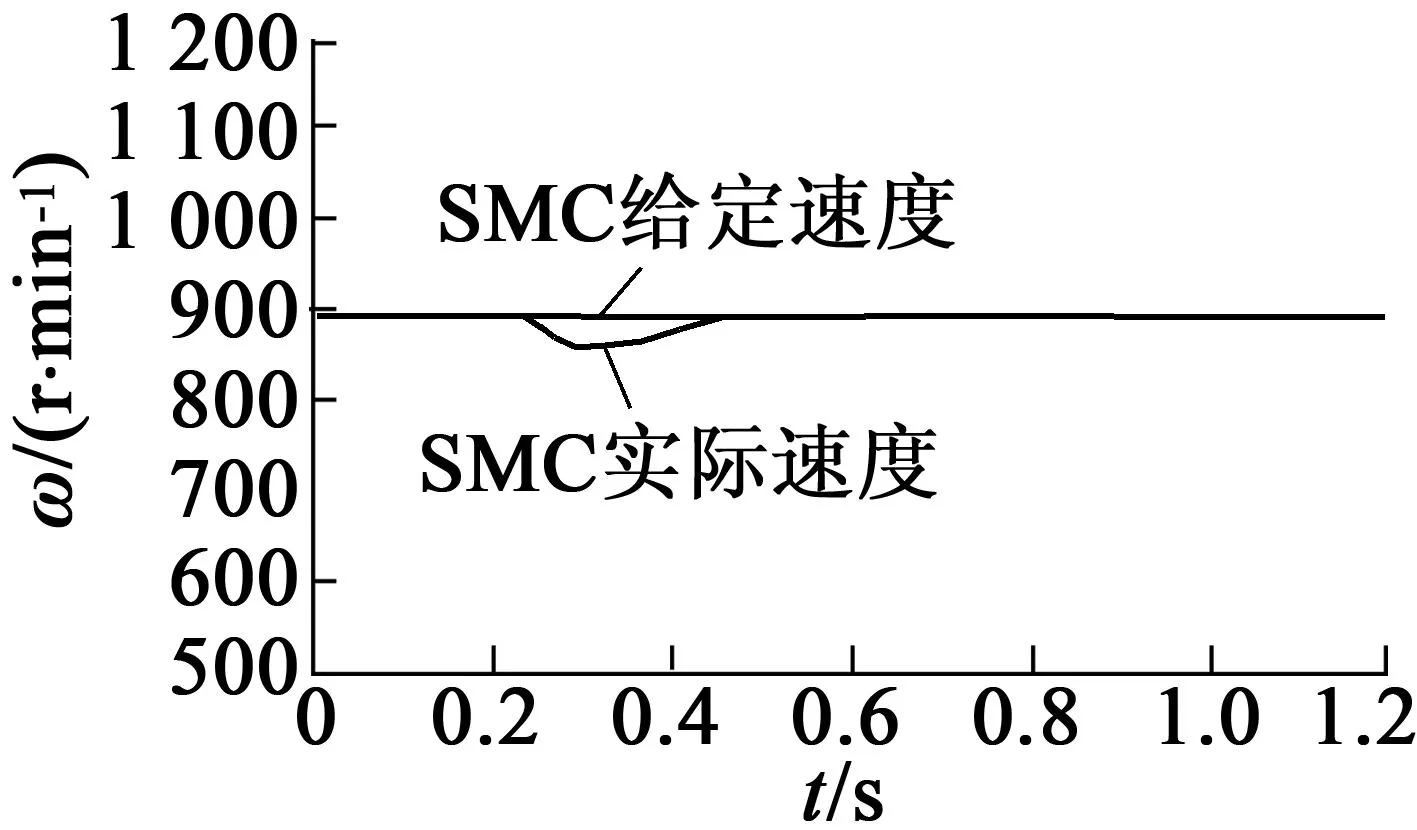
(a) SMC

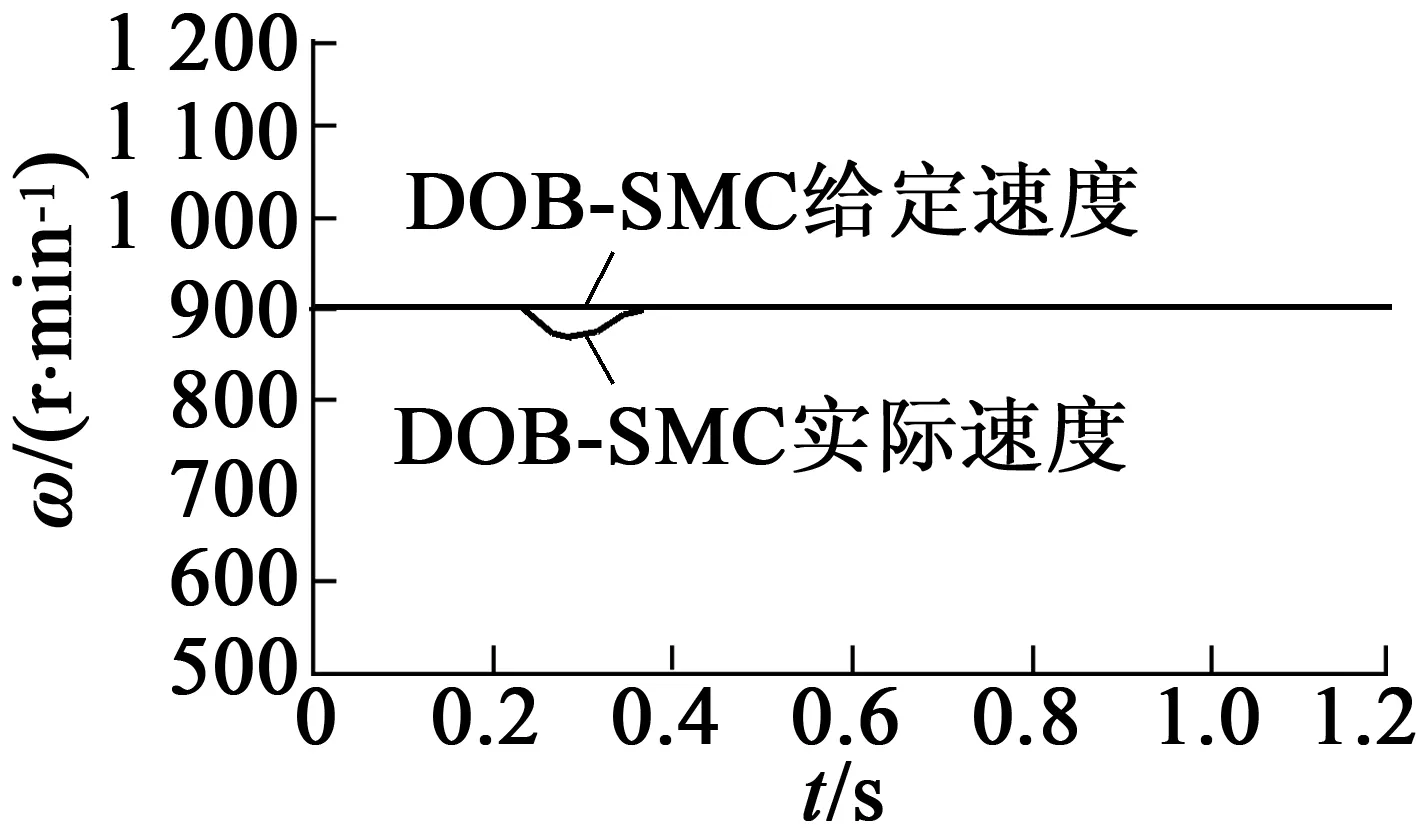
(b) DOB-SMC

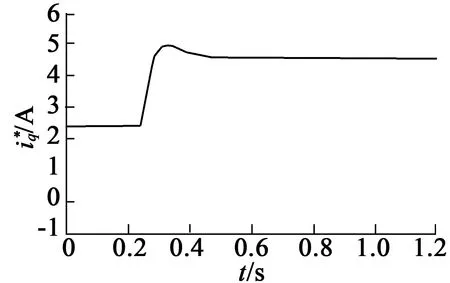
(a) SMC

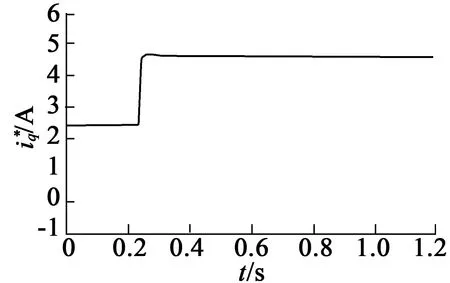
(b) DOB-SMC

4 結 語

本文采用滑模變結構控制與DOB相結合的控制方法，利用基于指數趨近律的SMC,進一步提高電機系統靜態和動態跟蹤性能，通過基于DOB的反饋控制器來補償負載干擾，提高系統的快速響應性，從而使PMSM控制系統具有更好的魯棒性。仿真與實驗結果表明，本文的方法與普通的滑模變結構控制相比，速度達到穩定的時間縮小一半，并且速度的過沖幅度進一步減小。因此本文的方法具有較高的跟蹤精度和響應速度，對參數變化和外部擾動的魯棒性強,具有較高的綜合控制性能。