基于諧波分析的永磁電機齒槽轉矩抑制

杜曉彬，黃開勝，黃 信

(廣東工業大學，廣州 510006)

0 引 言

隨著高性能永磁材料的出現，以及現代電機控制技術的發展，永磁電機在國民經濟各部門的運用越來越廣泛。永磁電機采用磁鋼產生機電能量轉換所需要的磁場，具有結構簡單、體積小、運行可靠等特點[1-2]。然而，由于電樞開槽，當定轉子產生相對運動時，磁鋼與定子齒部的相互作用會引起電機內磁場儲能的變化，從而產生齒槽轉矩，導致輸出轉矩波動，引起電機振動和噪聲，并影響電機的控制精度，因此如何有效地削弱齒槽轉矩一直以來都是專家學者研究的熱點之一。

削弱電機齒槽轉矩的方法有多種，例如采用斜極或者斜槽的方法、采用不等槽口寬度的方法、采用磁極偏移的方法、對偏心距或者極弧系數進行優化的方法等[3-7]，其中，開輔助槽削弱電機的齒槽轉矩是一種有效便捷的方法。傳統的開輔助槽的方法一般采用均勻開槽，即輔助槽在定子齒冠上均勻分布，每個電樞齒冠開1～3個輔助槽；或者采用有限元仿真的方式對輔助槽的位置、深度、寬度進行單變量參數優化掃描分析，得出最優的輔助槽參數，進行開槽。傳統的方法難以確定開槽個數和最優的開槽位置，且當采用有限元法對位置進行確定時，花費時間較長。

本文采用解析法與有限元分析相結合的方法確定輔助槽參數。通過對齒槽轉矩進行傅里葉分析，得到齒槽轉矩的各次諧波，利用解析法確定輔助槽的開槽位置和個數，使得特定位置和個數的輔助槽產生的齒槽轉矩諧波分量能有效抵消原有電機齒槽轉矩的基波和低次數諧波。輔助槽槽口寬度采用與普通槽槽口寬度一致，并利用有限元方法分析了最優的輔助槽深度，從而達到抑制齒槽轉矩的目的。以一臺12槽10極的永磁同步電機為例進行仿真分析，驗證了本文方法的有效性和正確性。

1 電機的齒槽轉矩分析及輔助槽開槽方法

根據電機學原理，當定轉子產生相對運動時，由于定子齒與磁鋼產生相互作用，磁鋼極弧中部與定子齒之間磁導基本不變，而磁鋼兩側與定子齒之間磁導變化較大，導致電機磁場儲能變化，從而產生了齒槽轉矩。齒槽轉矩被定義:

(1)

式中:W為電機磁共能;α為定轉子相對位置角。

當電機不斜槽或者斜極時，可將齒槽轉矩展開為傅里葉表達式[8-9]:

(2)

式中:Tn為齒槽轉矩的傅里葉系數;Ns為電機旋轉一周齒槽轉矩的周期數，其值為電樞槽數與極數的最小公倍數，即Ns=LCM(2p,Q)。

當電機定子齒上開輔助槽時，相當于改變了電機的極槽配合，同樣也影響了Ns的大小。由式(2)可知，齒槽轉矩的周期取決于Ns，隨著齒槽轉矩的周期數變大，則頻率越高，振幅越小，選擇合適的輔助槽數，能有效抑制齒槽轉矩的幅值。

為了簡化分析，在分析時認為輔助槽的影響與普通定子槽影響一樣，且本文只討論矩形槽。由于電機總的齒槽轉矩可以認為是每個磁鋼所對應的齒槽轉矩的疊加[10]，故本文將開輔助槽的電機分為2個次級結構進行分析。如圖1、圖2所示，以一臺12槽10極電機在齒冠上開一個輔助槽為例，第一部分為電機定子槽部分的次級結構，第二部分為電機輔助槽部分的次級結構，兩部分則可以合成一個完整的開槽電機的定子鐵心。當電機開輔助槽時，電機總齒槽轉矩為第一部分次級結構對應的齒槽轉矩與第二部分次級結構對應的齒槽轉矩的疊加。則第一、二部分次級結構對應的齒槽轉矩:

(3)

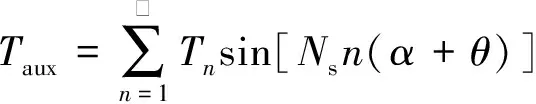
(4)

式中:θ為沿著電機旋轉方向普通槽組與輔助槽組相差的位置角。當電機開輔助槽時，電機總的齒槽轉矩:

Tcog=Tslot+Taux

(5)

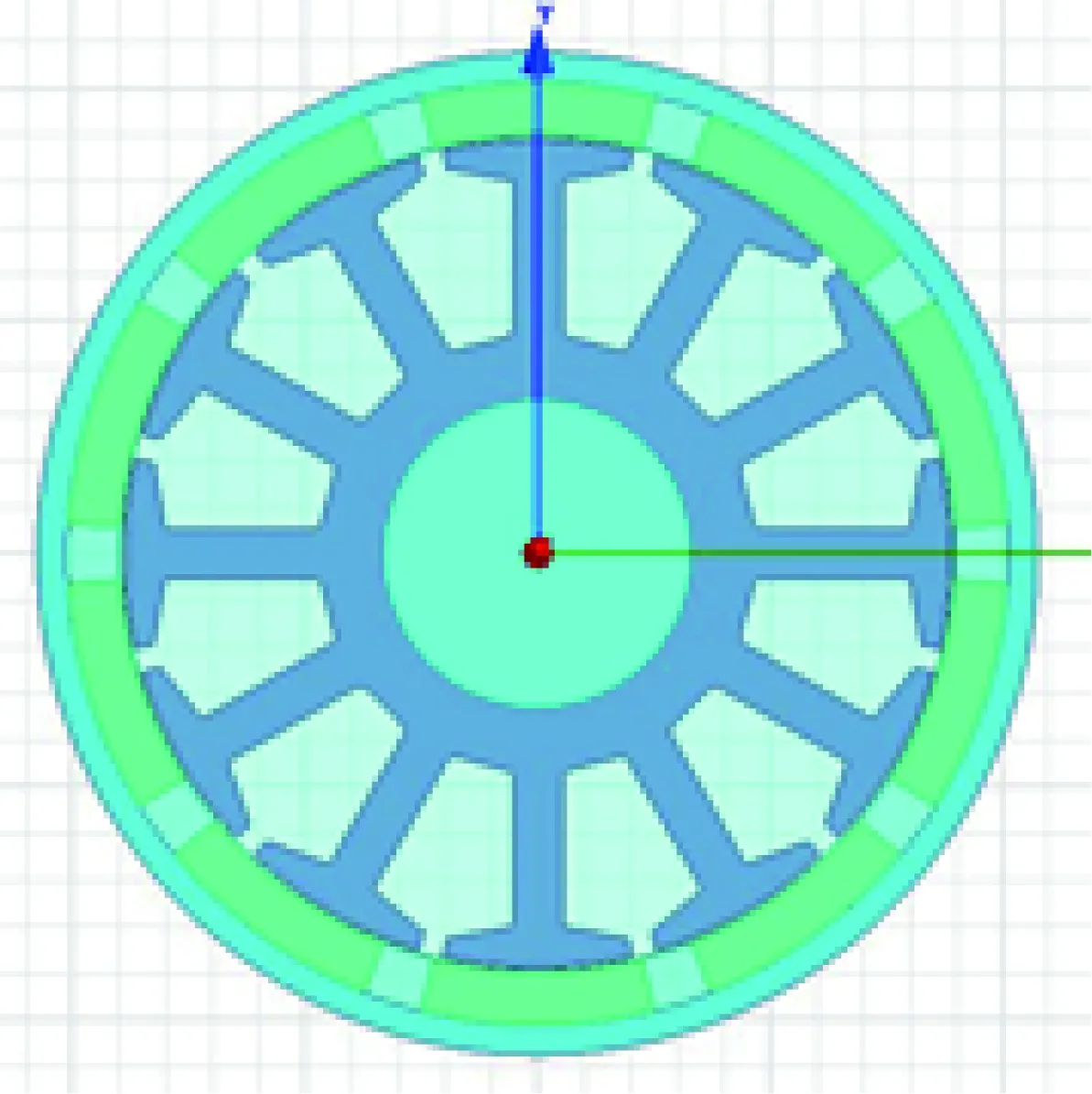
圖1 第一部分次級機構

圖2 第二部分次級機構

為了使得輔助槽對應的齒槽轉矩的一次諧波能對電機原有的齒槽轉矩的一次諧波產生抵消作用，令θ取值:

(6)

式中:k為非負整數，且由于θ1取值不能超過一個齒距，故k≤Ns/Q。則當n為1時，將式(6)代入式(5)，可得到Tcog一次諧波分量為0，電機原有齒槽轉矩的一次諧波被完全抵消，只剩下二次及以上的諧波。

為了抑制n次諧波，可選在不同的位置開一組輔助槽，令θ取值:

(7)

式中:k為小于等于nNs/Q的非負整數。則將式(7)代入式(5)，可得到Tcog的n次諧波分量為0，電機原有齒槽轉矩的n次諧波被完全抵消。

由于不均勻的槽口寬度以及不均勻的槽分布會引進新的諧波[11]。對于式(6)、式(7)，k取值有多個，即抑制n次諧波輔助槽的位置可以有多種選擇，應該按照如下原則選取：同一個齒冠上開的輔助槽，應使得輔助槽開口依齒冠中心線呈對稱；對于電機上所有的輔助槽與普通槽，應使得輔助槽槽口與普通槽開口在鐵心表面盡量均勻分布。而對于輔助槽槽口寬，應選取與普通槽槽口寬一致。為了簡化分析，分析時將輔助槽與普通槽的影響等效，而實際上，輔助槽的影響并不等同于普通槽的影響，故可以通過有限元方法對輔助槽深度進行參數優化掃描分析，選取能抑制原有齒槽轉矩的基波以及n次諧波的最優輔助槽深度。

2 有限元仿真分析

為了進一步分析和驗證本文方法的正確性與有效性，本文以一臺12槽10極的電機為例進行有限元仿真分析，通過在合適的位置上開輔助槽，抑制電機原有齒槽轉矩的基波以及二次諧波，從而抑制齒槽轉矩幅值。

2.1 永磁同步電機齒槽轉矩分析

本文采用的12槽10極電機基本參數如表1所示，采用ANSYS Maxwell 2D軟件建立電機模型，并對電機原有的齒槽轉矩進行仿真分析，由圖3可知，齒槽轉矩的幅值為52.784 4 mN·m。對齒槽轉矩進行傅里葉分析，得到各次諧波幅值分布如圖4所示，可以看出，較大的諧波分量主要集中在基波和二次諧波，第三至六次分量很小，其中，基波分量幅值為49.186 2 mN·m。

表1 電機模型基本參數

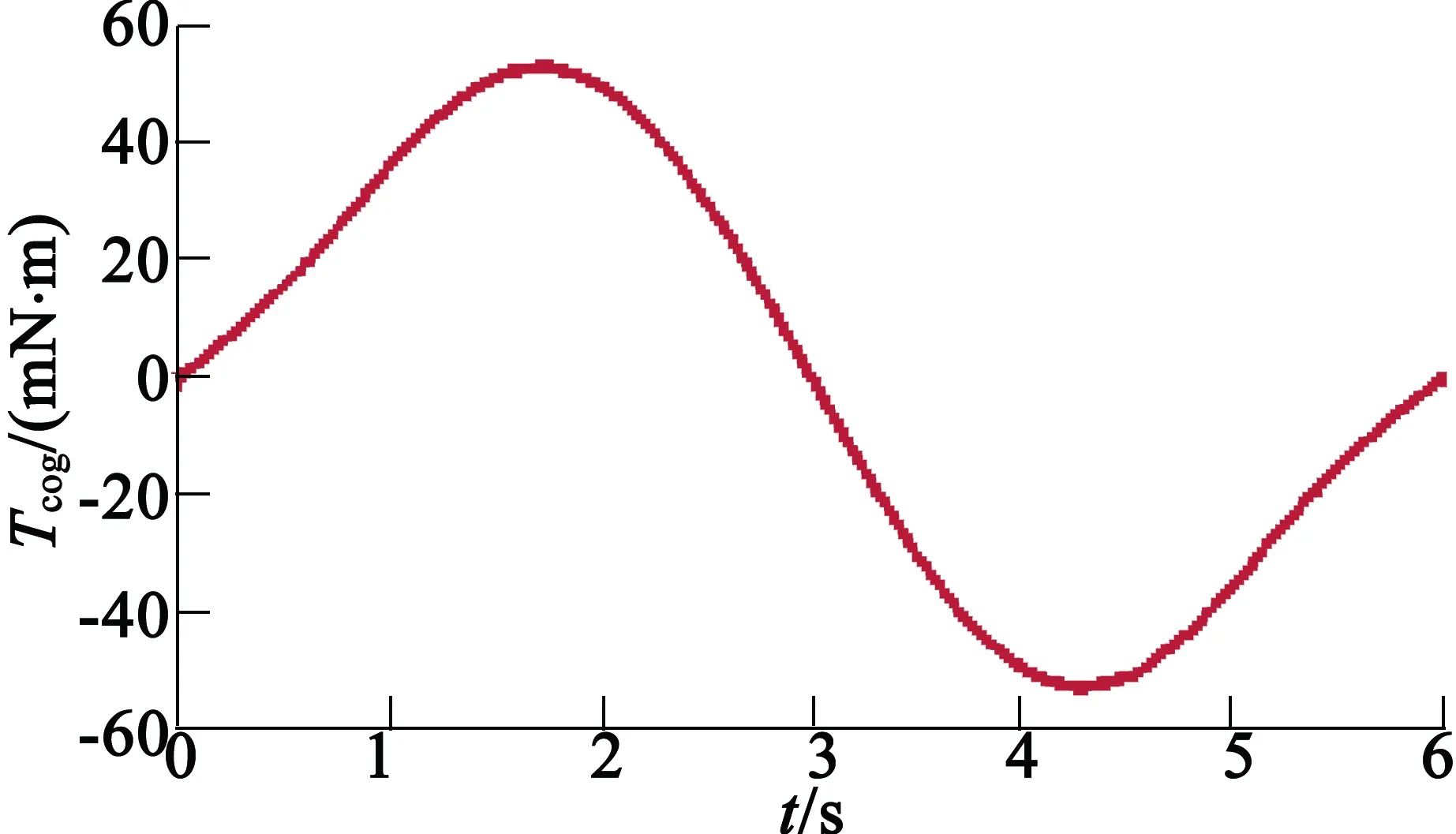
圖3 優化前電機齒槽轉矩波形

圖4 優化前電機齒槽轉矩各次諧波分量

2.2 輔助槽位置分析

采用本文的抑制方法進行分析，對于12槽10極的分數槽電機，槽數與極數的最小公倍數Ns為60，即定子旋轉一周產生的齒槽轉矩周期數為60，且每個定子齒對應的機械角度為2π/Q=30°。對于基波，采用式(6)進行計算，且注意θ取值不能超過一個齒寬，則θ取值為3°,6°,15°,21°,27°，即每一組的輔助槽開槽位置應與普通槽偏移以上計算度數。以一個齒冠為例子，如圖5所示，可以看出，開槽的位置是關于齒槽中心線呈現對稱分布的，且15°對應的輔助槽位置剛好位于齒冠中心線上。

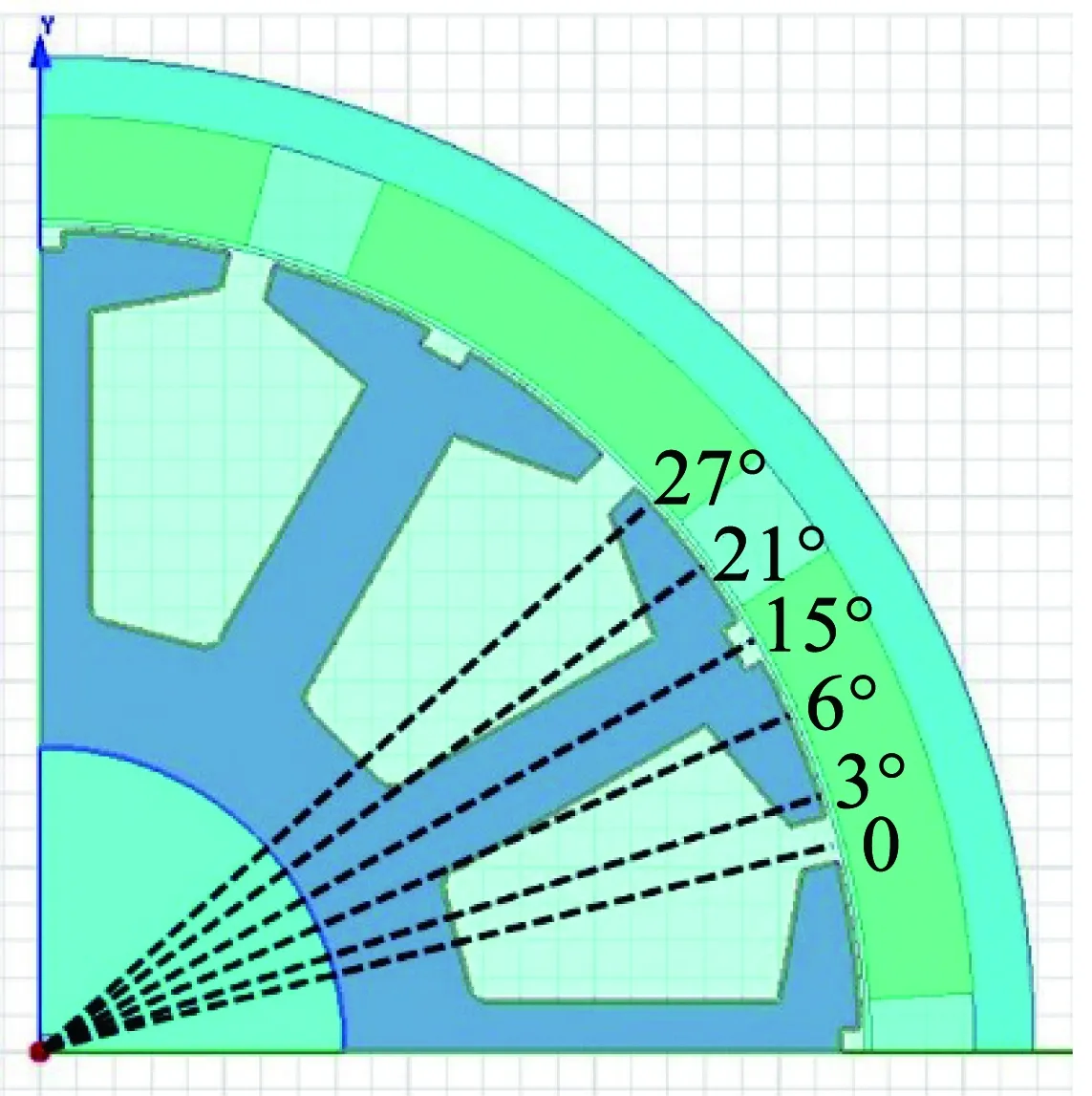
圖5 抑制基波的輔助槽開槽位置

采用輔助槽槽口寬與定子槽口寬度一致，槽深為1 mm，由于在3°,27°時輔助槽與定子槽重合，仿真分析在6°,15°,21°時3個不同位置開輔助槽時電機總齒槽轉矩，即每一組的輔助槽開槽位置與普通槽偏移以上度數，如圖6所示。可以看出，3個波形基本一致，說明開槽效果基本相同，只有細微不同。其中，15°位置的總齒槽轉矩最低，為15.870 2 mN·m。對波形進行傅里葉分析，得到各次諧波幅值分布如圖7所示。可以看出，電機原齒槽轉矩基波被明顯抑制，然而，二次諧波明顯升高，這是因為輔助槽對應齒槽轉矩的二次諧波對電機原齒槽轉矩二次諧波起到疊加作用，使其增大。對比不同開槽位置下的諧波分析結果，發現15°位置的總齒槽轉矩前三次諧波幅值皆比其他2個位置開槽時的總齒槽轉矩前三次諧波幅值低，其中，15°位置基波分量輔助為1.629 2 mN·m，比未開槽前有明顯的下降，說明比均勻開槽以及依齒冠中心線開槽效果要好。故對于齒槽轉矩的基波，當開一組槽時，可選取15°位置進行開槽；當開兩組槽時，可選取6°和21°位置同時進行開槽，但是這種開槽方式使得普通槽與輔助槽在鐵心表面分布不均勻，效果較差；當開三組槽時，可在6°,15°,21°位置同時進行開槽。

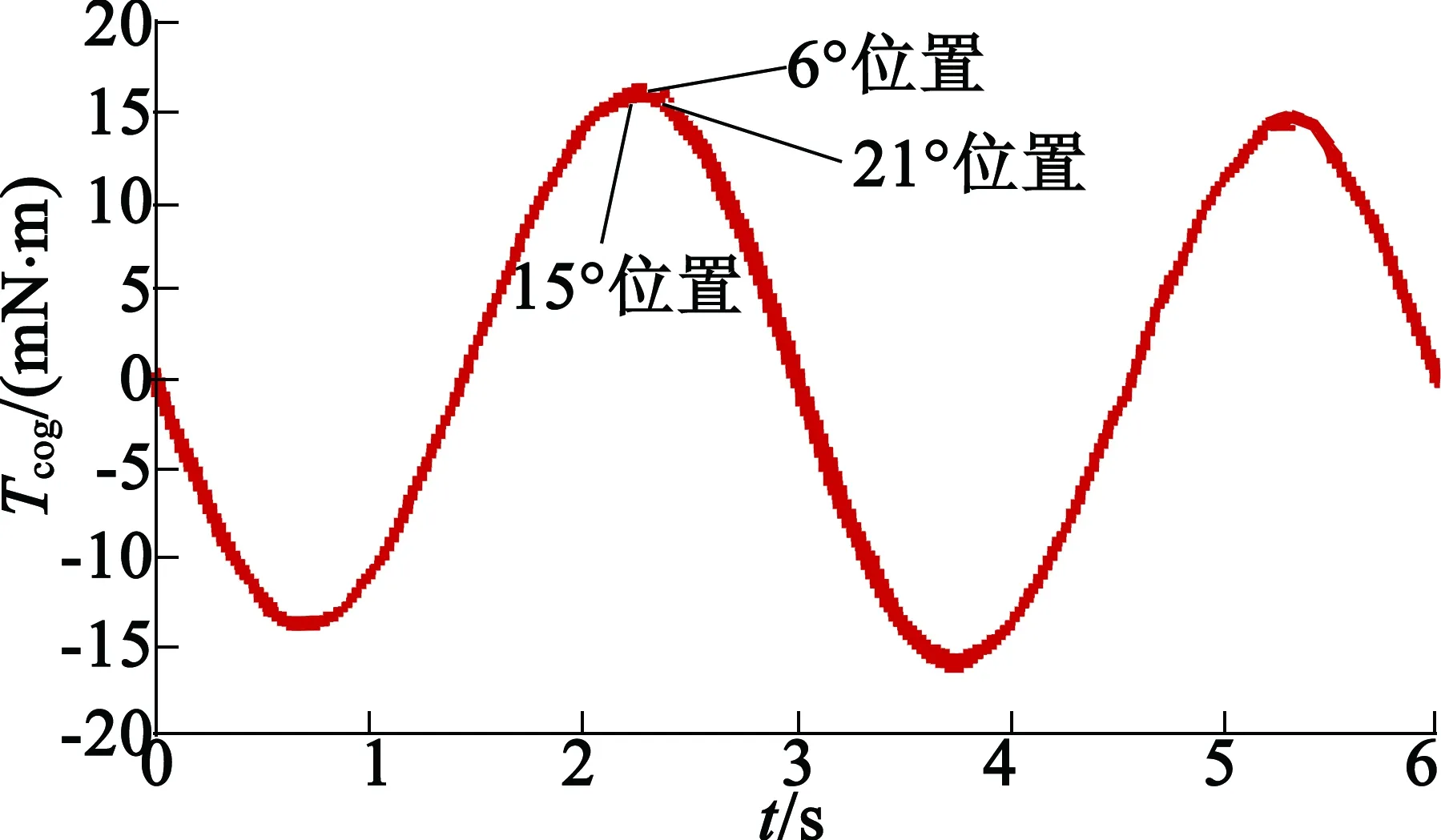
圖6 不同位置開槽的電機總齒槽轉矩波形

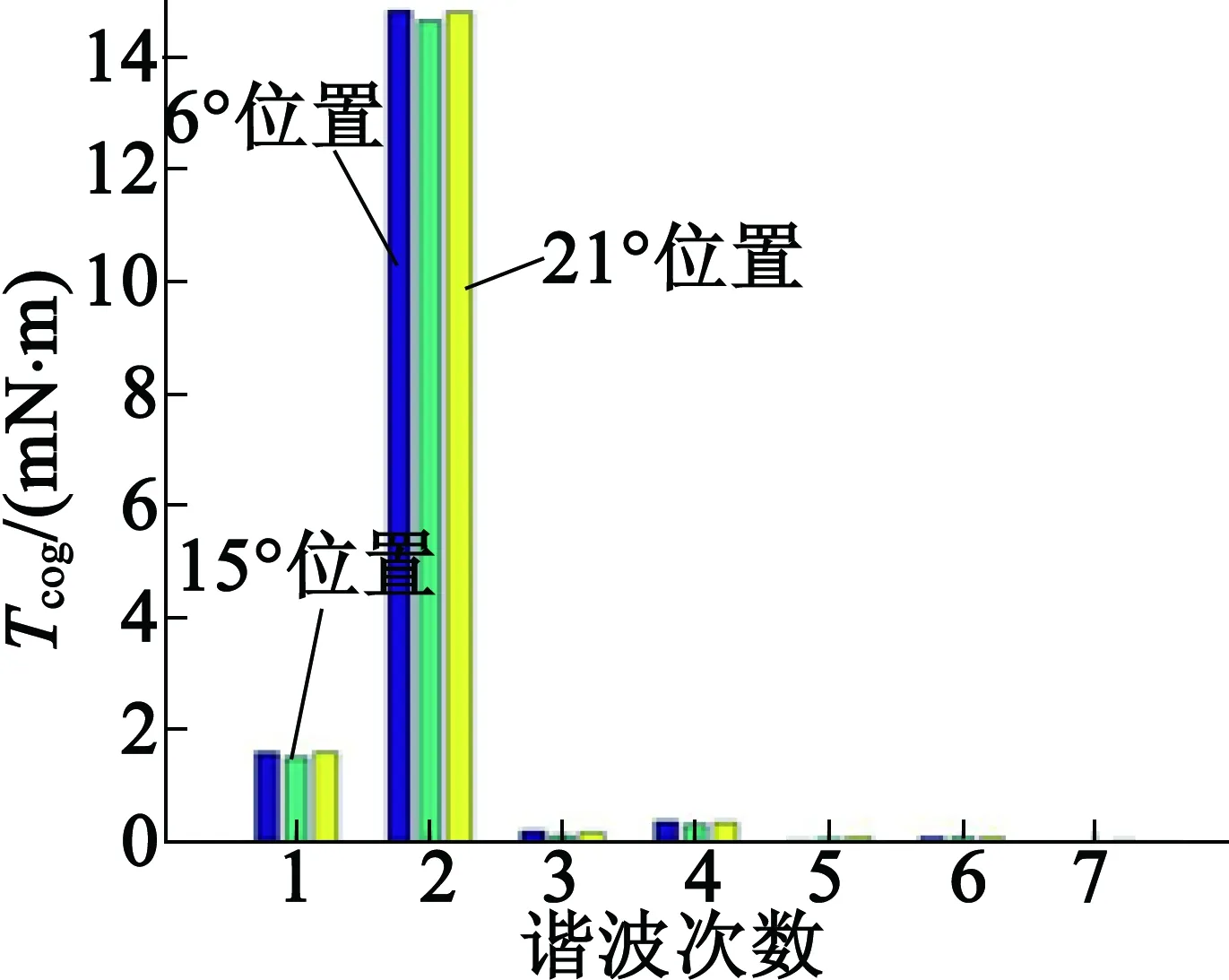
圖7 不同位置開槽的總齒槽轉矩諧波分布

2.3 齒槽轉矩基波及二次諧波抑制分析

根據上述的分析結果，為了簡單方便，選取開一組槽，且在15°位置開槽。為了進一步確定最優的輔助槽深度，采用有限元軟件參數優化分析的方法對輔助槽深度進行掃描，槽深取值范圍為0.1～1.5 mm，得出最優的輔助槽深度為1.1 mm，如圖8所示。可以看出，電機總齒槽轉矩為15.125 7 mN·m。對波形進行傅里葉分析，得到各次諧波幅值分布如圖9所示，基波分量幅值為0.031 9 mN·m，電機原齒槽轉矩基波分量基本被抵消，二次諧波分量為14.913 3 mN·m。

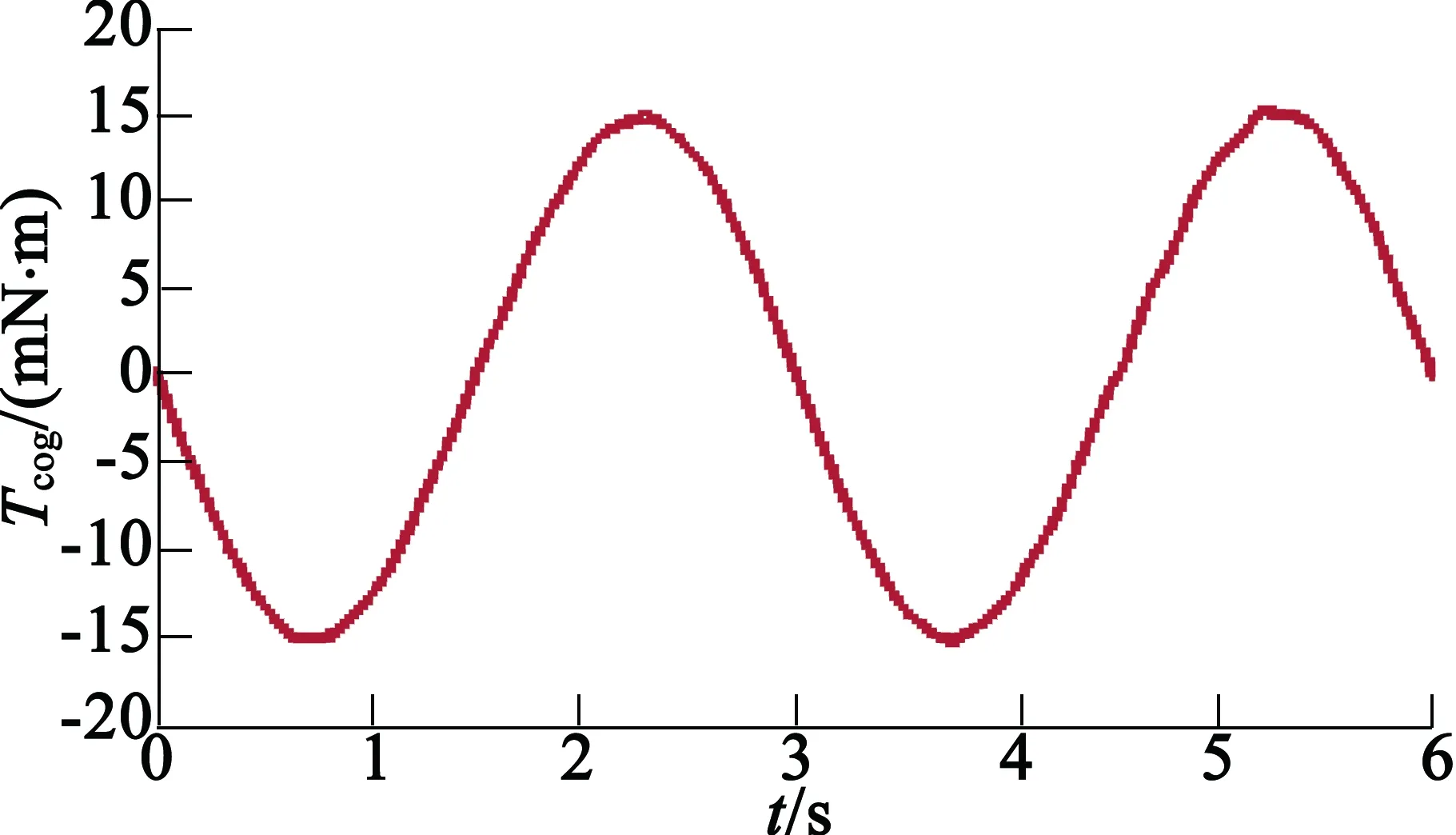
圖8 抑制基波后電機總齒槽轉矩波形

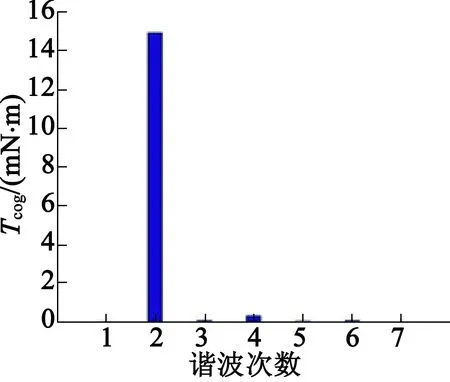
圖9 抑制基波后電機總齒槽諧波分布

為了進一步抑制電機原齒槽轉矩二次諧波，采用式(7)進行計算，n取2，且注意θ取值不能超過一個齒寬，則θ取值為1.5°,4.5°,7.5°,10.5°,13.5°,16.5°,19.5°,22.5°,25.5°,28.5°，按照盡量均勻開槽和依齒冠中心線開槽的原則，選取7.5°和22.5°位置開槽，并使新的輔助槽與15°位置輔助槽槽深一致，采用有限元分析參數優化方法對槽深重新進行掃描分析，取值范圍為0.1～1.5 mm，得出最優的輔助槽深度為1.2 mm，電機總齒槽轉矩取最低幅值為1.519 8 mN·m，比電機原齒槽轉矩幅值下降了97.12%。圖10和圖11分別為優化前后電機齒槽轉矩波形對比和傅里葉分析。從圖10可以看出，齒槽轉矩幅值明顯下降。對波形進行傅里葉分析，得到各次諧波幅值分布，如圖11所示，基波分量以及二次諧波分量幅值分別為0.011 3 mN·m,1.020 8 mN·m，相較于電機原齒槽轉矩，分別下降了99.97%,87.56%，前兩次諧波得到明顯抑制。

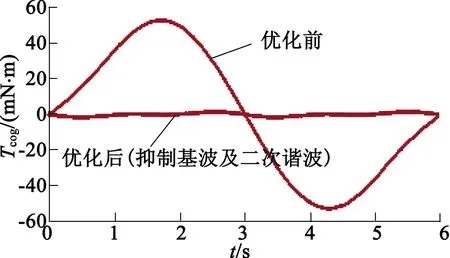
圖10 優化前后電機齒槽轉矩波形對比

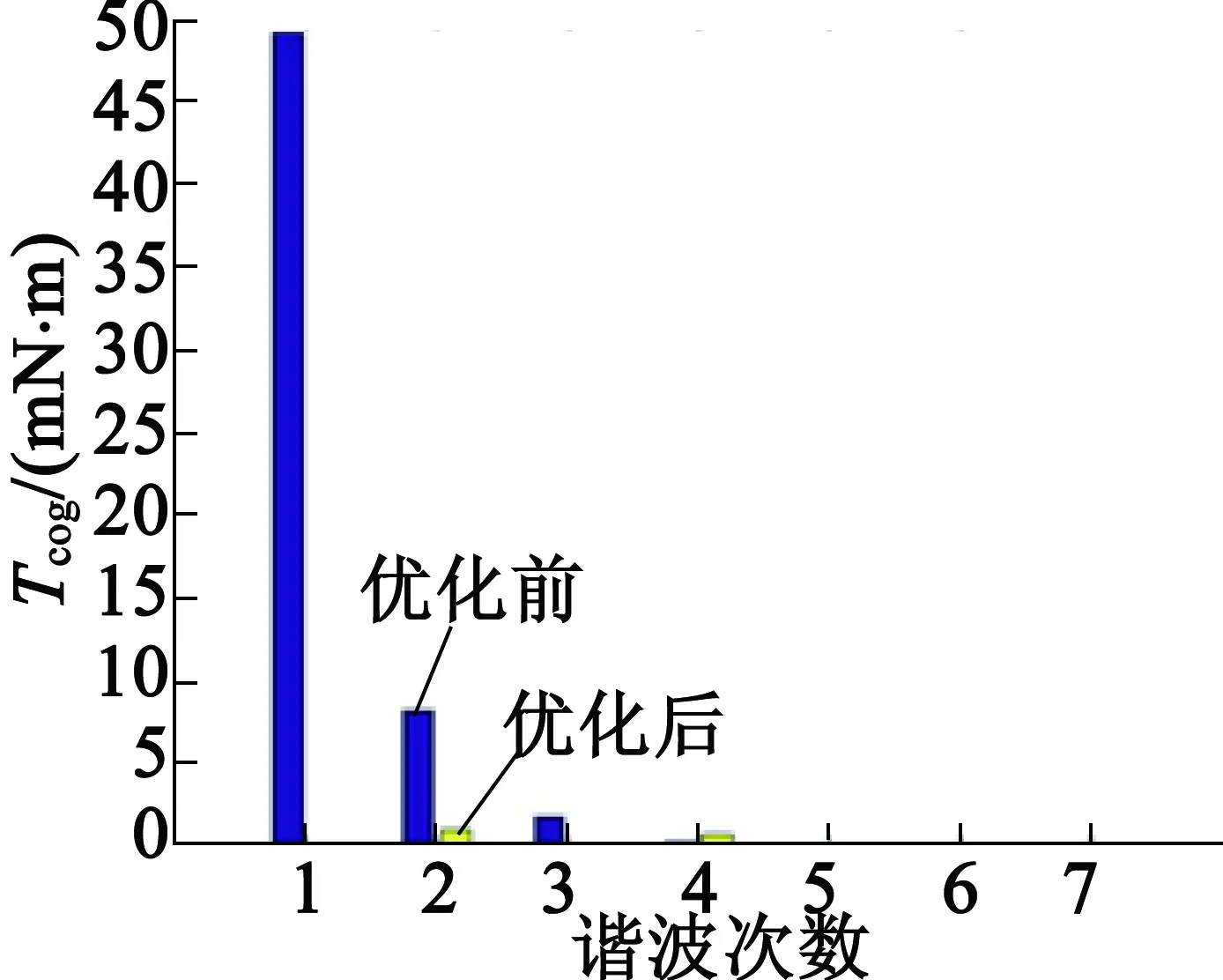
圖11 優化前后電機總齒槽轉矩波形諧波分布對比

3 結 語

本文對齒槽轉矩進行了諧波分析，采用解析法與有限元法相結合的方式，研究了一種抑制齒槽轉矩的方法：對電機原齒槽轉矩進行傅里葉分析；利用輔助槽對應的齒槽轉矩諧波分量抵消電機原齒槽轉矩的基波和低次數諧波，并給出了抵消基波和n次諧波的開槽位置的具體公式和選取原則；輔助槽槽口寬采用普通槽槽口寬度，并利用有限元法分析了最優的輔助槽深度。以一臺12槽10極電機為例進行仿真分析，結果表明，采用本文的方法能有效抑制齒槽轉矩的基波和低次數諧波，使得齒槽轉矩幅值明顯下降。