基于雷管實際延時范圍的逐孔爆破振動合成計算與應用
吳昊駿,龔 敏
(北京科技大學土木與資源工程學院,北京 100083)
近年來對城市隧道爆破振動控制趨于高安全指標,需要精確設置爆破參數。由于隧道常用多孔微差爆破,藥量、微差間隔時間與合成振速存在復雜的耦合關系,研究多段微差合成振速計算方法,對城市隧道爆破設計具有非常重要的意義。
自1985年Anderson[1]提出用單孔爆破振動數據計算微差合成振速以來,這一原理被廣泛應用。Blair和Hinzen發展了線性[2]、非線性疊加方法[3];吳從師等[4]以臺階單孔爆破振動曲線為源函數,計算兩孔時差0和25 ms的合成振動曲線,證實同段延時誤差影響合成振速和單孔爆破振動波形具有重復性。徐全軍等[5]用單孔樣本函數對某爆破工程振動峰值預報,發現若在混凝土試驗中精確控制兩孔微差時間,則計算與實測波形吻合較好;陳士海等[6]研究兩孔微差爆破不同時間的合成振動波形變化規律,指出微差時間為爆破主振1/2周期時振動降幅最大;其他學者[7-12]也進行了相關研究工作。
目前的困難是隧道實際微差爆破振動計算難以實現,以雷管段號時間計算合成振速誤差很大。由于雷管各段均有延時范圍,在此范圍內將隨機產生多種振動疊加,隨著微差孔數不斷增加形成海量的合成振動曲線。若從爆破精準控制與安全考慮,應分析全部振動組合,再按安全振速下最大振動曲線設置參數。但這涉及巨大的計算量且過程復雜,在過去不可能完成。為簡化計算龔敏等提出在最初兩孔起爆延時范圍內計算所有可能振動曲線,選其中最大振速曲線再與第3起爆孔的延時時段內各時刻進行振動合成,以此類推最終曲線可視為多孔微差最大合成振動曲線[13]。然而最大振動曲線是否是由前段峰值曲線與后段延時范圍內逐次疊加形成,仍有待進一步研究。
計算技術的發展給解決上述問題提供了可能,本文中以重慶渝中隧道工程為背景,根據各段雷管實際延時范圍設計計算程序并優化算法,成功解算出8孔微差爆破百萬種以上全部合成振動組合,分析了各段延時誤差對振速影響;在研究第二臨空面形成時間后提出城市隧道爆破藥量計算新方法。
1 方 法
1.1 各段雷管段別延時范圍的確定與振動合成曲線數量關系
如上所述,以名義段號時間進行微差振動合成計算不能滿足城市精準控制爆破需要,本文先解決各段雷管起爆延時時間的測定問題,龔敏等[14]研究發現雷管樣本的延時數據可代表批次雷管基本特性,據此以重慶渝中隧道工程為例,對各段雷管樣本進行延時起時間測試。
首先確定各段雷管延期時間Δti的取值范圍。在同一批次雷管中,每段隨機抽取數個樣本實測起爆時間,在各段實測結果中篩選出最早起爆時間Ti,earl及最遲起爆時間Ti,lat。得到第i段雷管起爆時間Δti范圍:
Δti∈(Ti,earl,Ti,lat)i=1,2,3,…
(1)
式中:Δti為第i段雷管起爆時間;Ti,earl為第i段雷管起爆時間最小(早)值;Ti,lat為第i段雷管起爆時間最大(遲)值。
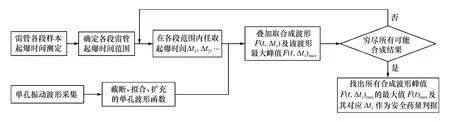
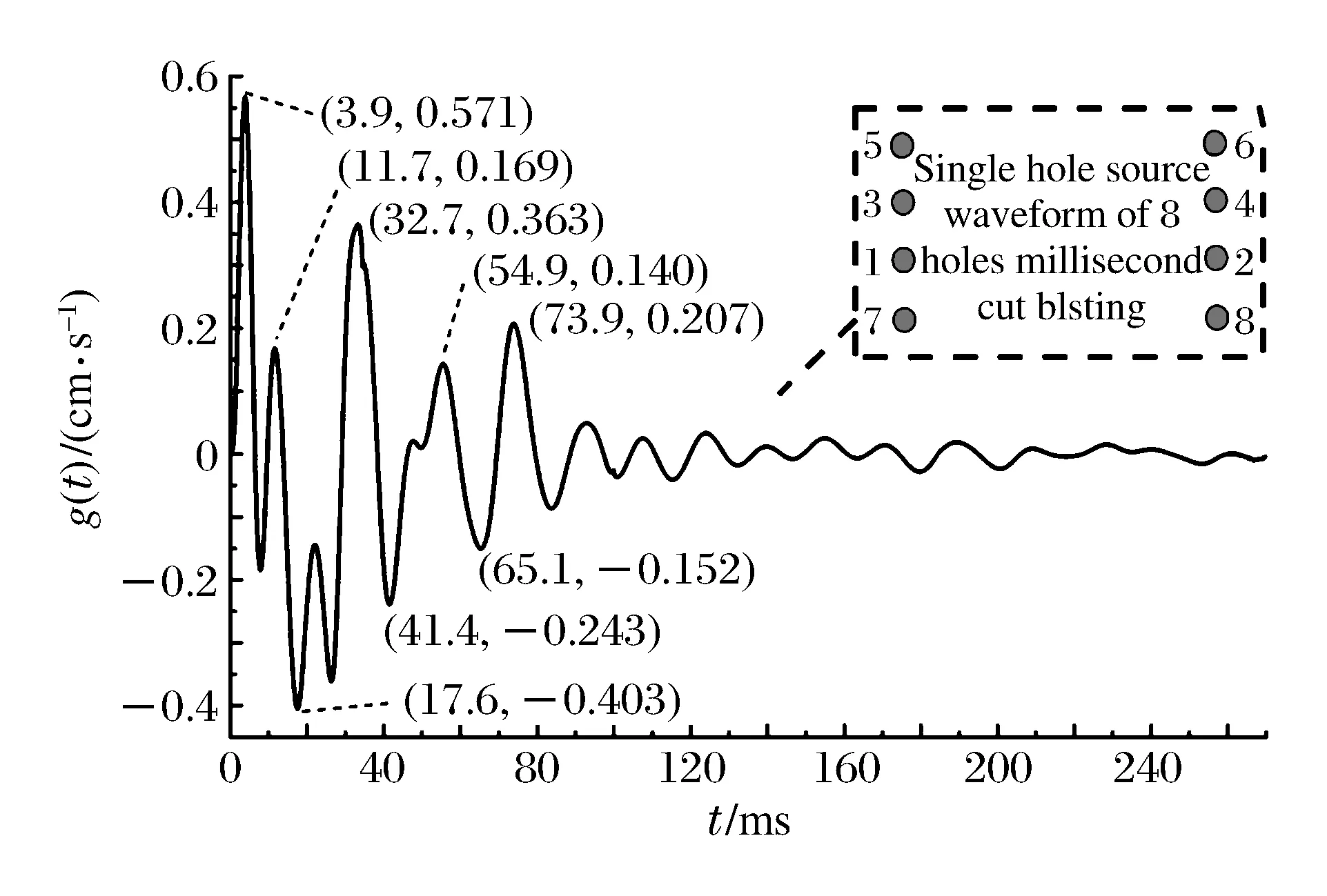
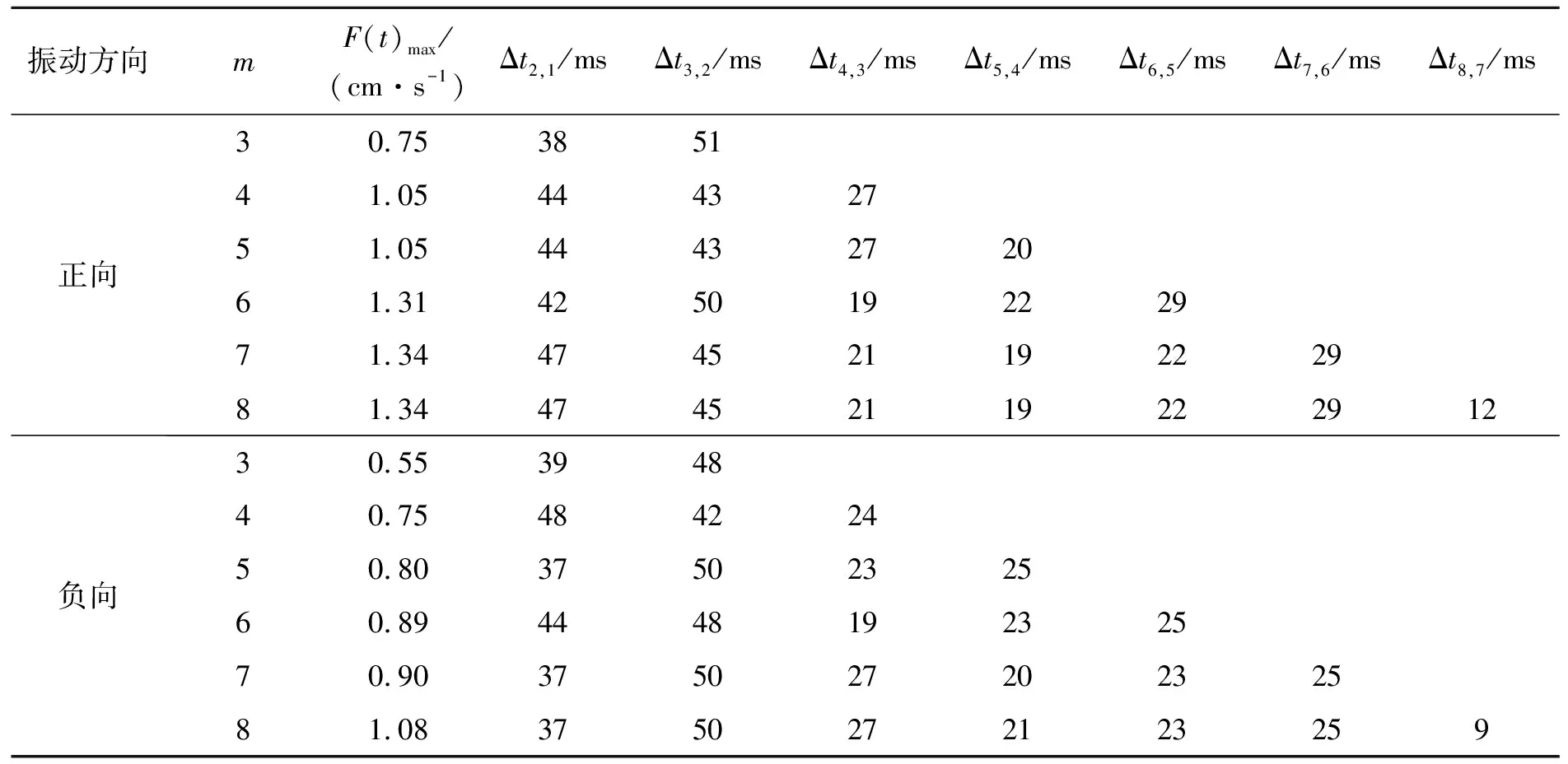
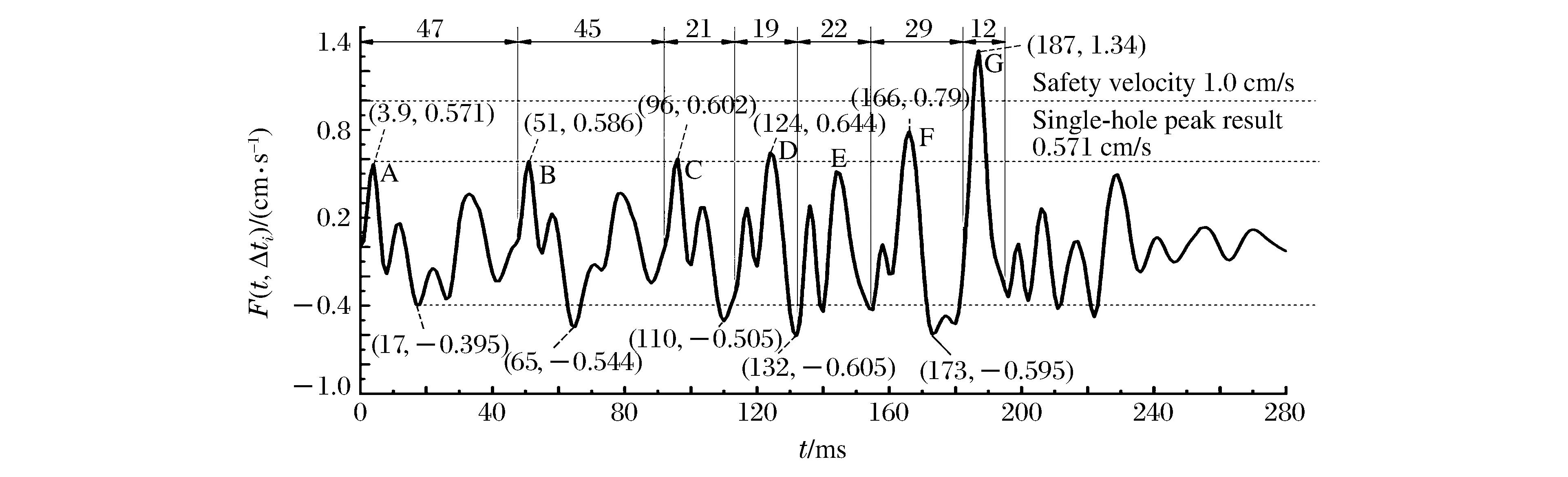
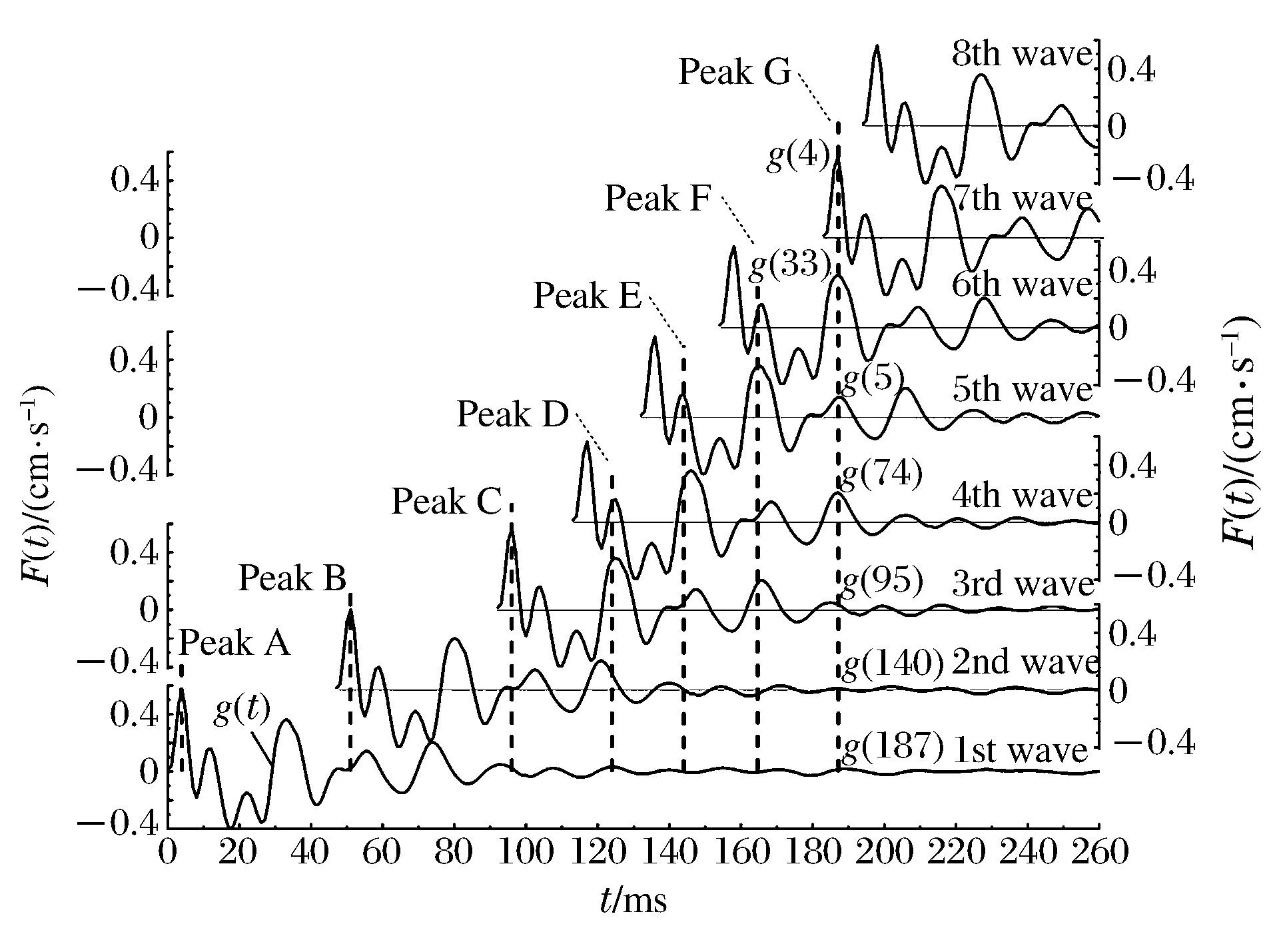
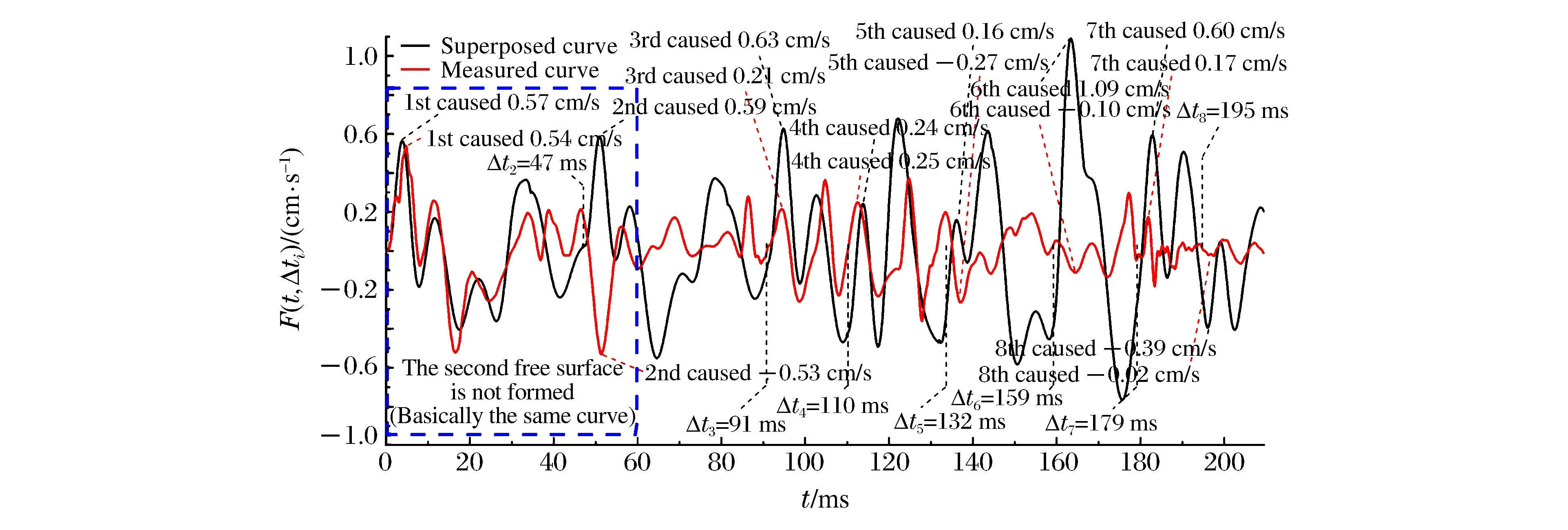
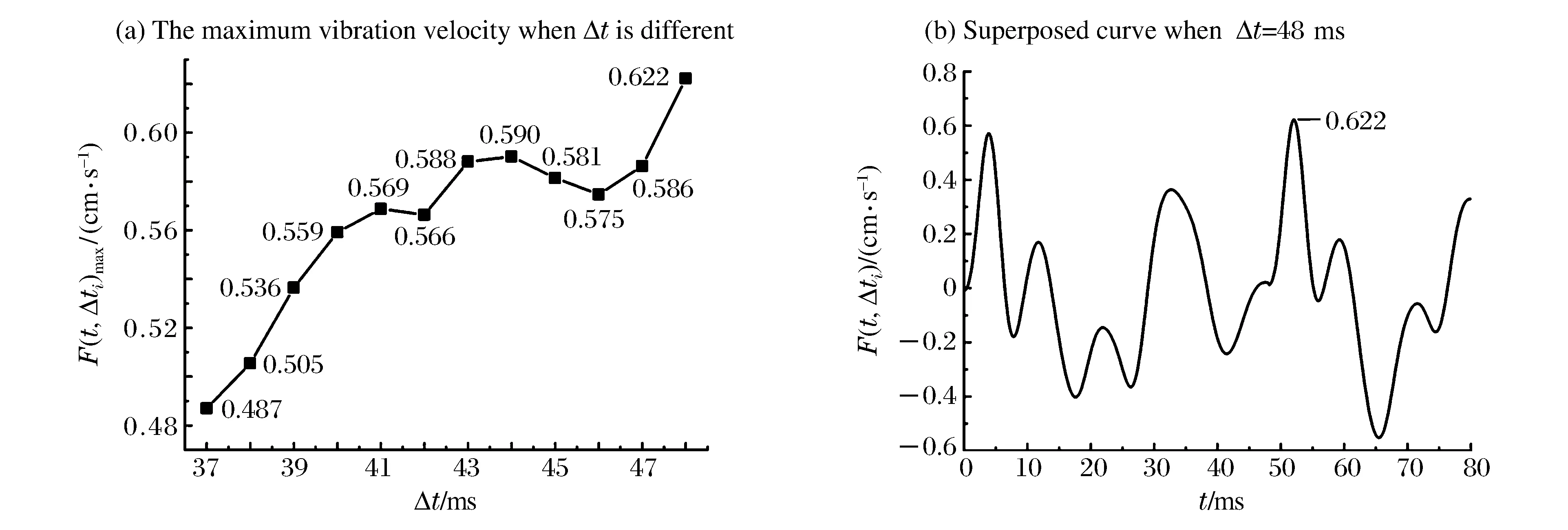
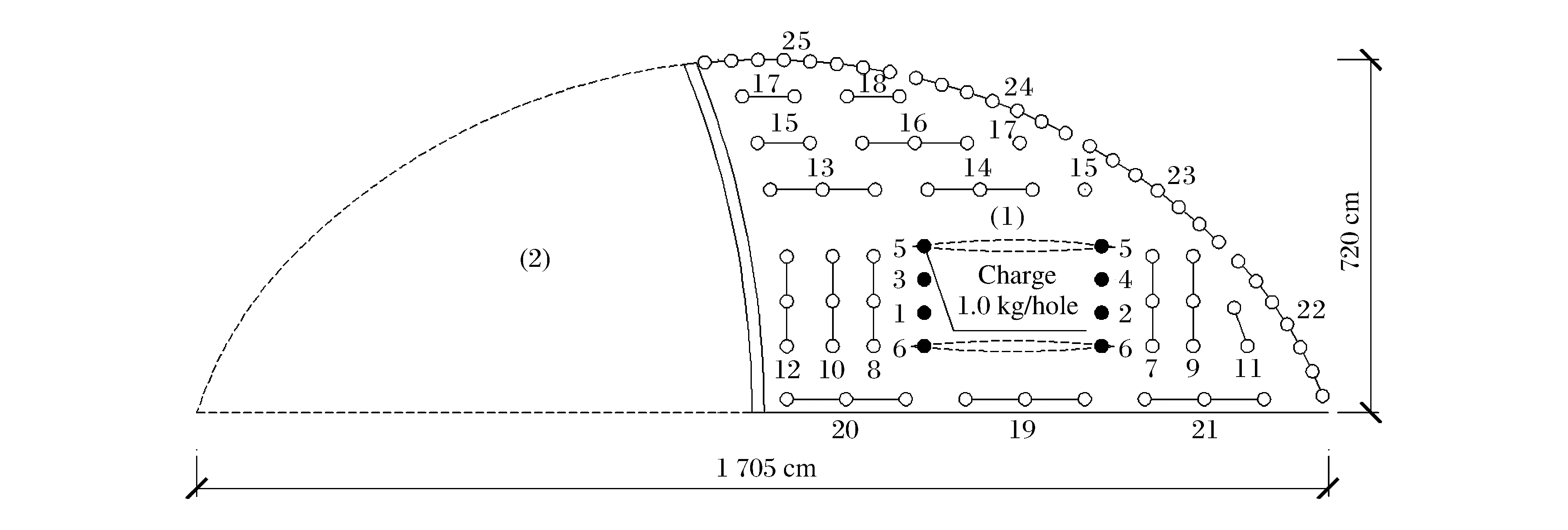
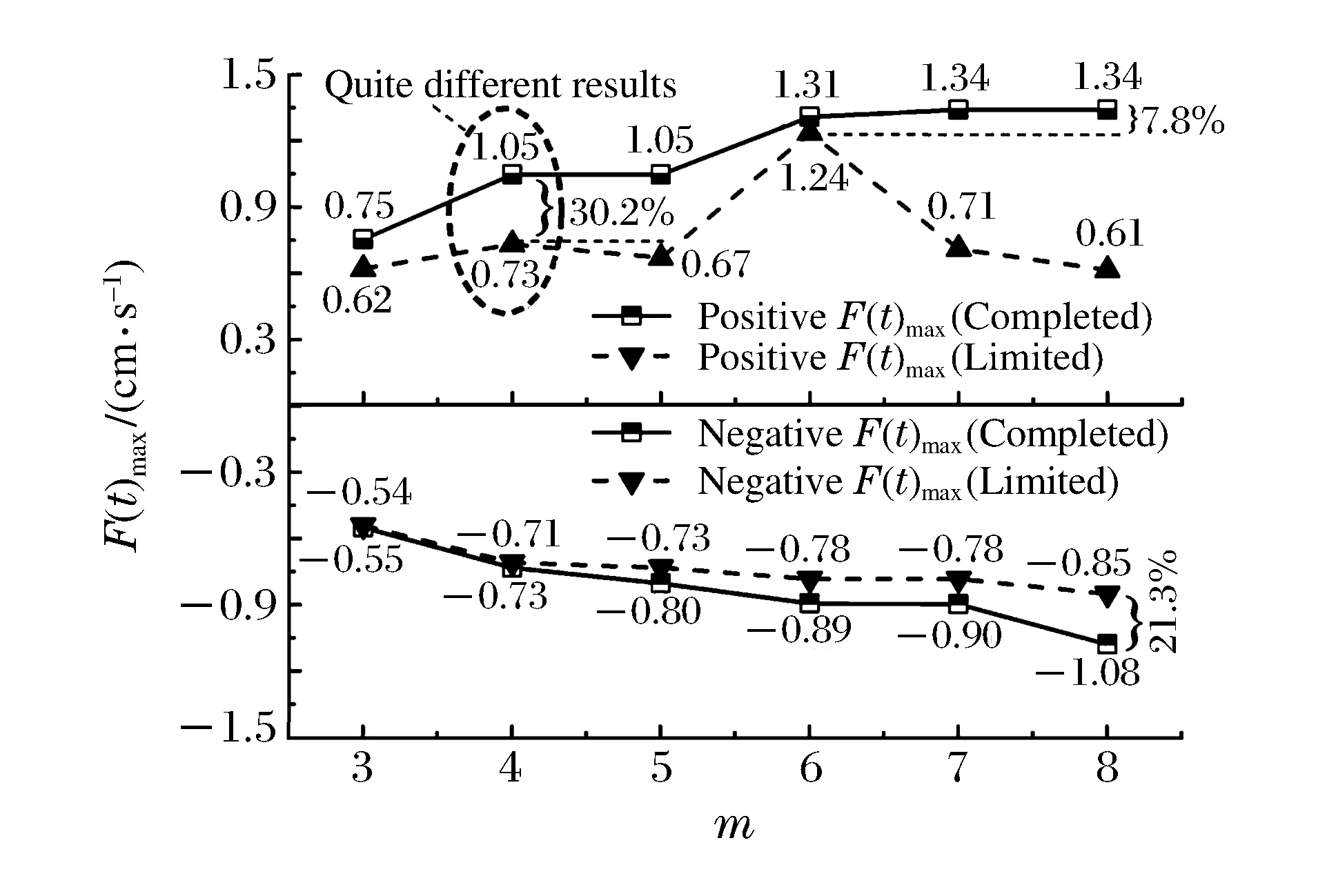
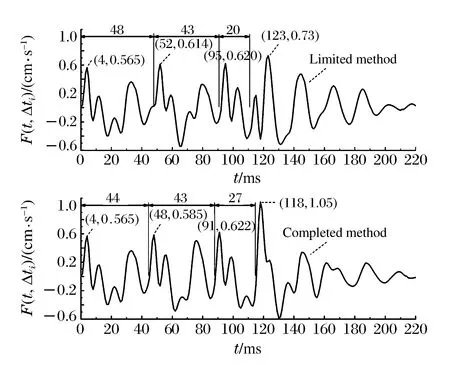
數據組中若存在Ti,earll 由實測雷管起爆時間得到段間微差時間Δti,i-1的范圍: Δti,i-1∈(Ti,earl-Ti-1,lat,Ti,lat-Ti-1,earl)i=2,3,4,… (2) 圖1 渝中隧道工程各段雷管起爆時間實測圖Fig.1 Initiation times of detonators tested in Yuzhong tunnel project 重慶渝中隧道采用基于第二系列高精度非電雷管開發的定制25段非電雷管,每段取10個樣本測試并記錄數據,現設計采用8孔逐孔掏槽爆破,找出各段雷管最早起爆時間Ti,earl和最遲起爆時間Ti,lat。篩除易串段雷管段別后重新編號,這種個別跳段盡可能避免了段數減少,新的1~8段雷管起爆時間范圍如圖1所示,其中實測1段雷管無延時誤差。 若在這8段雷管各實測延時范圍內進行8孔逐孔掏槽,可能的微差爆破組合有114萬余種(微差間隔以1 ms計)可能性,即存在114萬種以上不同的合成振動曲線,以往由于工作量巨大及計算機軟硬件發展限制,全部振動曲線難以計算獲取和比較,必須采用新的方法加以解決。 在主要測點采集的單孔爆破波形,包含周圍地質條件、爆區環境信息。受介質阻尼等因素的影響,波速最終會衰減為0。從初至波到幅值Amax/e(Amax為最大振幅,e為自然對數的底)處為波形主振段,持續時間為tmain。 疊加前對單孔波形進行時長截取,將截斷時間t0之后的振速歸零。該值太大,程序運行時間過長,獲取結果緩慢;該值太小,最大疊加振速出現時,前期起爆的單孔波形振速可能已歸零,計算不準確。因此保證最后一段波主振段結束時,首段波速剛好歸零即可,即: t0=Tm,lat+tmain (3) 式中:t0為單孔波形截斷時間;m為參與疊加的雷管總段數;Tm,lat為第m段(最后一段)雷管實測最遲起爆時間;tmain為單孔波形主振段持續時間。 編寫MATLAB程序,將所截波形擬合成傅里葉級數形式,便于程序分析處理: (4) 式中:g(t)為單孔波形擬合函數;t為時間;n為級數;ω為基頻;a0、aj、bj為擬合系數。 確定波形函數,實際上就是確定式(4)中基頻值和各系數值: 式中:N為采樣點個數;k為分點;tk為采樣點橫坐標;g(tk)為采樣點縱坐標。 將式(4)擴展到時間全域,使各列波在任意疊加時刻均有意義: (5) 式中:f(t)為擴展的單孔波形函數;t為時間;t0為截斷時間。 在不考慮第二臨空面作用的前提下,按線性疊加理論對該藥量單孔波形進行疊加,預測多孔合成波形及最大振速。對垂直振速分量進行疊加時,波形同向,可進行代數疊加: (6) 式中:F(t,Δti)為按起爆時間組Δti疊加得到的波形函數;m為參與疊加的雷管總段數; Δti為第i段雷管起爆時間。 至此,通過公式(6)再利用MATLAB軟件多級For循環語言計算編程,可獲得在各段延時時段內、多孔微差爆破所有可能合成振動組合的曲線。 如上所述,按照式(6)循環嵌套各段雷管Δti取不同值,獲取所有波疊加后可能得到的時間-振速曲線F(t,Δti)后,找出該Δti組合下,各波形曲線F(t,Δti)的最大峰值F(t,Δti)max。 在眾多F(t,Δti)max中,找出最大值F(t)max及對應Δti組合,為疊加最不利情況對應的最大振速: F(t)max={F(t,Δti)max}max (7) 在眾多F(t,Δti)max中,找出最小值F(t)min及對應Δti組合,為疊加最有利情況對應的最大振速(微差降振效果最好的情況): F(t)min={F(t,Δti)max}min (8) 需要注意的是:為了找出最大合成振動曲線對應的合成峰值F(t)max及各段起爆時間Δti,程序在計算過程中需要保存大量的數據,普通計算機或服務器硬件配置無法滿足如此龐大的數據存儲需求。對此本文通過優化算法壓縮數據存儲量,成功完成了程序計算。 利用求得的各段起爆時間Δti,可求得各段微差時間Δti,i-1,其值應在式(2)確定的區間內: Δti,i-1=Δti-Δti-1(i=2,3,4,…) (9) 將以上步驟表示為流程,如圖2所示。 圖2 合成計算流程Fig.2 Superposition calculation process 以渝中隧道工程為例,搭載Xeon W3680 CPU、24 G內存64位計算機作為研究平臺,將參與疊加的波列數與對應計算機運行時間列于表1中。由表1看出隨著參與疊加波數的增加,計算機程序運行時間也不斷增加。 表1 計算機運行時間統計Table 1 Statistical results of computer running times 據此結合計算機能力,通過波數較少的波形疊加耗時估計波數較多時程序運行的時間。方便合理調整微差時間的迭代間隔及波形的采樣間距。 以上計算實例表明,在計算機正常配置下,考慮雷管各段延時范圍的8孔微差爆破全部合成振動曲線計算時間為4.2 h,故對所有可能的微差合成爆破振動曲線分析處理可行,可作為今后爆破設計的參考。 計算8孔微差爆破振動最大值及相應的振動曲線只是精準設計重要的一環,這一方法只考慮了多段微差間隔對合成振速影響,沒有涉及第二臨空面形成對振速影響,將二者結合才能實現掏槽藥量精準設計。 (1)第二臨空面形成時間的確定 在筆者過去研究[13]基礎上,現場實測逐孔逐段掏槽爆破振動曲線1,根據EMD法[15]結合爆前實測獲取各段雷管準確起爆時刻;以此8個確定時刻及單孔單自由面爆破振動測試計算8孔微差爆破合成振動曲線2,由于曲線2沒有考慮第二臨空面對振速影響,將曲線1、2進行同時刻振速差異對比即知第二臨空面形成時間,也即知第二臨空面形成前的雷管段數m0。 (2)爆破應用 上述計算完成后,再根據需要以相同藥量改變起爆間隔、不同藥量起爆間隔固定兩種方式進行設計應用:(a) 若只進行一次單孔爆破實驗,對m0以前各段按逐孔爆破重復1.3計算過程,所有振動曲線的最大峰值如都不超安全振速則以其中最大藥量為設計藥量;若有任一振速超標則改變微差間隔(跳段)再進行計算直到獲取安全藥量; (b) 進行不同藥量(一般2~3次)隧道單孔爆破振動測試,對m0以前各段按逐孔爆破重復1.3計算過程,選取所有振動曲線峰值不超標的最大藥量作為設計藥量,即實現控制振速下循環進尺最大化。 按傅里葉級數對測點采樣數據進行擬合,得到單孔波形及掏槽孔分布情況如圖3。其中正向最大振速為0.571 cm/s (3.9 ms),負向最大振速為-0.403 cm/s (17.6 ms),均未超過現場1.0 cm/s的安全振速要求。 圖3 掏槽區布孔及單孔爆破振動波形Fig.3 Arrangement of cut-holes and single-hole vibration wave 參考波形衰減程度及計算機的運行能力,根據式(3)確定單孔波形主振段74 ms,結合第8段雷管最遲起爆時間195 ms,取前270 ms的采樣數據進行分段擬合如式(10),編程計算傅里葉系數: (10) 式中:ω1、ω2為基頻;a01、aj1、bj1、a02、aj2、bj2為擬合系數;t1為分段時間,取130 ms;t0為截斷時間,取270 ms。 第一段,樣本均值6.21×10-4,函數樣本均值3×10-4,樣本方差0.026,函數樣本方差0.026;第二段,樣本均值-2.81×10-5,函數樣本均值-2.04×10-5,樣本方差1.44×10-4,函數樣本方差1.44×10-4。擬合效果較好。 以現場雷管樣本實驗得到的各段起爆時間Δti的范圍為基礎,暫不考慮第二臨空面的消振效果,將第2列波、第3列波……第8列波,按照各起爆時間范圍內的Δt2、Δt3……Δt8循環嵌套疊加,得到微差各段延時范圍內所有可能的合成振動曲線,表2為程序計算的8孔微差爆破后形成的最大合成振速F(t)max及其對應的Δti,i-1組合。 表2 最大合成振動速度及對應微差時間組Table 2 Maximum superposed vibration velocity and corresponding millisecond times 按8列波疊加正向最不利情況計算得出的Δti,或按進一步求出的Δti,i-1=47,45,21,19,22,29,12 ms對各單孔波形進行疊加后,得到圖4所示8孔微差起爆可能形成的最大合成振速曲線,各段微差起爆時刻為最不利起爆時差組合,這一計算結果為結合第二臨空面形成進行爆破設計奠定了基礎。 圖4 8波疊加正向最不利情況時預測波形Fig.4 Worst predict waveform superposed by eight waves 圖5 各幅值分量與單孔波形對應關系Fig.5 Corresponding relations between velocity components and single waveforms 波振動至187 ms(G峰)時,正向最大振速為1.340 cm/s,超過1.0 cm/s的安全振速要求,為單孔爆破最大振速的2.35倍,其余微差時間組合得到的最大振速都小于該結果,該組合為疊加最不利情況;負向最大振速為-0.605 cm/s,雖未超過安全振速要求,但也達到單孔實驗負向最大振速的1.50倍。為進行比較,也按式(8)計算了降振最大的振動曲線,其峰值振速不大于單孔爆破最大振速。 所有振動曲線計算結果表明:同段延時范圍即使在較小范圍內,其合成振速之間的差異也可達57%(1-(0.571 cm/s)/(1.34 cm/s)),這是非常有意義的研究結果,它說明按現在施工中常采用的以標稱段號設計爆破網絡,難以做到精確控制爆破振速。 起爆187 ms時G峰出現,第8列波尚未出現,前7列波按照起爆時差參與振動。各列波貢獻的幅值分量,表現在單孔波形(圖3)上,分別等于g(187)、g(140)、g(95)、g(74)、g(55)、g(33)、g(4)。由于持續振動了較長時間,前3列的幅值分量g(187)、g(140)、g(95)均小于0.01 cm/s,而第4~7列波振動時間不長,幅值分量g(74)、g(55)、g(33)、g(4)相對較大(圖5),做出了主要貢獻。單個波幅值分量雖然不大,但因為個數較多,且全部處于波峰處,導致合成振速也很大。 綜上,波形疊加作用早期,參與波數較少,合成振速取決于單個波形的較大波峰,后期參與疊加的振動波數量多,合成振速轉而取決于處于波峰的子波個數。個數較多時,小振速也可導致疊加中后期最大合成振速出現。如果沒有第二臨空面的減振效果,則只能采取分離波形的方法避免波的疊加。 以上計算得到8孔微差爆破振動最大值及相應的振動曲線,今后只需獲知雷管延時范圍和進行簡單的單孔爆破振動測試,即可解決類似多孔微差合成振動計算問題。然而要實現精準爆破設計,還需考慮第二臨空面形成對振速的影響。目前關于第二臨空面形成時間大多為經驗認識,一般認為在50~120 ms之間,隨現場地質條件和爆破參數不同而改變。本文用1.5節方法(1)確定第二臨空面形成時間后,再與計算合成振速曲線結合進行爆破設計。 通過EMD法結合爆前樣本實測數據,識別實測爆破振動曲線各段起爆時間后,按求得的Δti對8列單孔波形進行疊加計算(無延時誤差范圍),得到計算合成振動曲線,將計算合成波形與實測振動曲線進行對比,如圖6所示。 圖6 實測與合成爆破振動波形對比Fig.6 Comparison between the measured and superposed blasting vibration waveforms 從圖6可看出在虛線框內時段實測與計算合成曲線波形相似、走向一致,主要峰谷出現時刻與幅值差別較小;60 ms后,實測波形平穩衰減,合成波形顯示出疊加的效果,二者差異明顯。第4段起爆后正向實測峰值0.25 cm/s,為正向合成峰值0.79 cm/s的31.6%。第6段起爆后,正向實測峰值0.20 cm/s僅為正向合成峰值0.45 cm/s的44.4%。據此可以確定現場第二臨空面形成時間不超過60 ms。渝中隧道現場大量爆破振動測試數據均證實了這一結論的準確性。 通過以上分析可知,渝中隧道爆破第二臨空面形成時間為60 ms。從圖1可知,2段起爆延時范圍37~49 ms,3段起爆時段87~92 ms,故在第3段起爆前第二臨空面已經形成。因此只需進行1~2段延時時段內所有可能的微差爆破振動合成計算,以驗證振速是否超標即可。 重復本文1.3節過程,嘗試Δt2,1所有可能取值后發現:Δt2,1=48 ms時正向最大合成振速0.622 2 cm/s,滿足安全振速控制要求(如圖7所示)。1.0 kg判斷為安全藥量。由于現場條件與時間限制,現場只進行0.8 kg、1.0 kg單孔爆破實驗,沒有繼續嘗試1.2 kg單孔藥量實驗。在條件允許的情況下,應對不同藥量分別進行單孔實驗及爆破振動合成分析,選出同時滿足安全振速和循環進尺最大的設計藥量。 圖7 第二臨空面形成前波形合成Fig.7 Waveforms superposition before appearance of the second free surface 需指出的是,渝中隧道爆破時第二臨空面出現時間在3段雷管起爆前,但其他地點因地質條件和布孔參數變化而不同,如在更高段別m0段前形成,則應計算前m0-1段微差爆破所有可能的合成振動曲線,再選擇不同藥量設計安全藥量,也可在超標區間定向跳段改變起爆間隔以控制振速;在第二臨空面形成后則改為兩孔(多孔)同段起爆。 渝中隧道控制振速1.0 cm/s,左洞大斷面面積149 m2,設計用CD法爆破開挖。根據4.2節研究成果,在首爆1區掏槽孔藥量設計為1.0 kg,雖然第3段起爆范圍(87~92 ms)為第二臨空面形成以后,但考慮二者時間相近,為保險起見3段仍采用單孔單段掏槽,依據楔形掏槽孔位第4段相應為單孔單段;從第5段開始改為兩孔一段爆破,圖8為現場實際布孔圖。2015年12月在渝中隧道ZK14+165.5-ZK14+195段進行了16次爆破,所有爆破均進行了振動測試,其中最大振速0.90 cm/s,平均振速0.65 cm/s,與3.2節計算吻合較好。 圖8 設計CD法爆破開挖Fig.8 Blasting excavation design of CD method 如引言所述過去因條件所限,基于雷管各段延時誤差的逐孔微差爆破振動合成少有研究,龔敏等曾采用簡化算法[13]對8孔微差爆破進行了計算:在1~2段延時范圍內以1 ms為增量計算所有合成振動曲線,僅取最大峰值振動所在曲線(一條)與3段延時范圍內各時刻分別進行振動合成,以此類推得到8段起爆后的曲線被認定為最大合成振動曲線。然而這樣有限次計算方法是否可靠仍無法驗證。鑒于本文方法完整求出8孔微差爆破合成振動所有可能的振動曲線,自然也可準確獲得最大振速的振動曲線,下面將分析前述方法的準確性,為方便比較將過去方法稱為有限次疊加法,本文方法稱為完全疊加法。 取相同單孔爆破振動波形前270 ms采樣數據,進行有限次疊加法求最大振速,按正向疊加最不利情況,Δti,i-1=48,43,20,22,29,19,11 ms,按負向疊加最不利情況,Δti,i-1=48,40,25,23,25,17,17 ms。 圖9 兩種方法結果對比Fig.9 Compare the results of two methods 將兩種方法所得最大合成振速進行對比,對比結果如圖9所示,最左端為第3列波疊加振速對比,實線為本文完全疊加法計算結果,虛線為有限次疊加計算結果。由圖中可看出完全疊加法算出的全時段最大合成振速F(t)max普遍較大。當4列波疊加時最大合成振速差距可達到30.2%。為此針對4列波合成波形進行了對比分析如圖10所示。由圖10可以看出,按完全疊加方法所得波形最大振速峰值出現稍早,且比按有限次疊加方法所得波形的最大振速峰值高出0.32 cm/s。 圖10 兩種方法求四列波疊加波形Fig.10 Find superposed waveform of four waves by two methods 圖11 振速分量的位置關系對比Fig.11 Position relations comparison of velocity components 參考各列波幅值分量與單孔波形的關系(圖11),上面4列波為有限次疊加方法確定的子波,下面四列波為完全疊加方法確定的子波。可以看出:采用有限次疊加方法,由于確定Δt4,3時,Δt3,2、Δt2,1已經固定下來,可調整空間有限,導致第4列波只能以較小峰值g(12) 參與最不利情況疊加,而單孔最大峰值g(4)無法參與貢獻,二者幅值差距g(4)-g(12)=0.402 cm/s,是導致兩種方法求得正向最大合成振速差距0.32 cm/s的主要原因。 有限次疊加的簡化方法限制了各段微差時間共同作用的可能性,可造成疊加結果30%的差異。雖然在一些應用實例中采用簡化方法取得成功,是因為第二臨空面在60 ms已經出現,微差合成作用受到抑制。但對于其他工程若第二臨空面形成時間較長,形成前參與疊加波數多,該方法計算的藥量有可能超過安全振速,因此不具有廣泛適用性。采用本文完全疊加法窮盡所有可能合成振動后進行爆破設計更為準確。 (1)快速發展的計算機及相關技術展示了解決爆破難題的巨大潛力,有可能給爆破研究方法帶來新的變革。如過去因雷管各段均有延時范圍并隨孔數增加形成海量合成振動組合、導致多孔微差爆破振動計算的難題,本文設計計算程序并采用優化算法,在有限時間完成了8孔微差爆破上百萬種以上合成振動計算量,為精準爆破設計奠定了基礎,可以預計今后更大數據的計算將在爆破工程中發揮重要作用。 (2)提出了城市隧道低振速精確控制掏槽藥量設計的新方法,主要特點是考慮了各段雷管延時起爆誤差影響和多孔微差合成振動影響,可表述為:計算第二臨空面形成前各段延時范圍內所有可能振動曲線后,選擇峰值振速不超標的最大藥量作為設計掏槽藥量;第二臨空面形成前逐孔逐段掏槽;形成后多孔同段爆破;第二臨空面形成時間因地質條件和爆破參數不同而有差異,可用比較計算合成振動曲線與實測振動曲線間差異獲取。 (3)現在施工中常采用以標稱段號設計爆破網絡,本文以渝中隧道為例研究表明:同段延時誤差即使在較小范圍內,其合成振速之間差異也可達57%,因此按雷管標稱段號設計起爆順序做法難以做到城區隧道低振速精準控制爆破。 (4)比較過去的有限次疊加法與本文完全疊加法計算的微差爆破最大合成振速曲線,發現采用簡化計算最多可造成30%的失真。進一步分析表明:波數量較少時合成峰值取決于單個波形的較大波峰;數量多時取決于處于波峰的子波個數。因此有限次疊加法在第二臨空面形成前起爆段數少時計算較準確;起爆段別較多時則不能對該合成振速進行有效折減而誤差較大。采用本文方法則窮盡所有延時范圍內可能的合成振動,計算結果準確。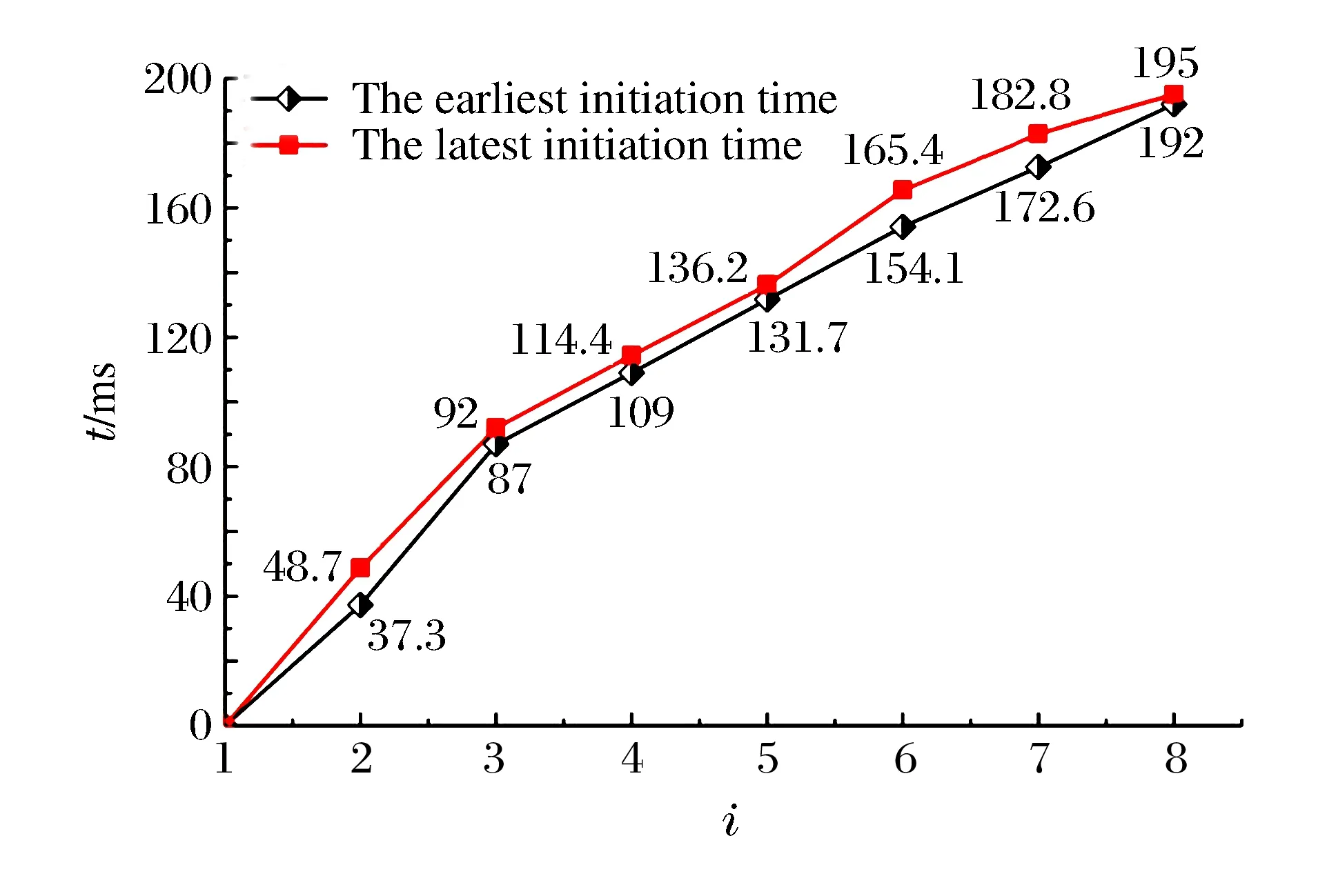
1.2 多孔微差振動合成的原理
1.3 疊加求振速最大值
1.4 計算機用時與程序運行可行性

1.5 結合第二臨空面形成時間調整爆破設計
2 振動合成計算實例
2.1 擬合疊加
2.2 合成波形分析
3 應 用
3.1 確定第二臨空面形成時間
3.2 根據第二臨空面形成時間進行爆破藥量設計
3.3 現場應用
4 兩種多孔微差爆破振動合成計算方法的可靠性比較

5 結 論

