青藏高原泥石流的形成及運動過程研究
王彬,張全貴
(青海省有色地質礦產勘查局八隊,西寧810001)
0 引言
泥石流主要是由砂、土、石等固態物質與水以及氣體組成的混合物,在重力的驅動下沿著山坡或者溝谷進行運動。泥石流具有來勢兇猛、爆發突然且破壞力極強的特點。泥石流屬于地質災害,其分布范圍很廣并且運動時間很長[1]。每年都會有泥石流發生,并且程度規模大不相同,給人們的生活帶來了重大的影響。根據調查發現,青藏高原是我國泥石流高發的地區,青藏高原的構造運動與氣候變化是引起泥石流高發的根本原因。青藏高原泥石流的發生,造成了巨大的經濟損失[2]。因此,本文主要對青藏高原泥石流的形成過程進行研究。
泥石流的破壞性較大,受到了社會以及學術界的重視,關于對泥石流的研究也越來越多[3]。傳統的泥石流模擬模型具有與實際情況吻合度較差的缺陷。因此根據收集到的資料與現場調查為數據,本文構建泥石流形成及運動模擬模型,對青藏高原泥石流的運動過程進行模擬與分析,為泥石流的防御與治理提供數據支撐。
1 泥石流形成運動模擬模型的構建
泥石流發生比較突然且破壞力極強,并且發生的地點往往較為偏遠,對于同一地點來說,其重復發生的間隔時間會很長,因此,泥石流發生的全過程很難被觀察到,這對泥石流的防御與治理及其不利。為了解決上述難題,構建泥石流形成、運動模擬模型[4]。首先建立泥石流形成、運動控制方程,然后采用數值分析法構建泥石流的模擬模型,通過計算機來模擬計算泥石流的形成、運動過程,將模擬結果呈現出來,為泥石流的防御與治理提供參考。
1.1 泥石流形成運動控制方程的建立
泥石流形成、運動模擬模型的前提是建設泥石流在運動的過程中質量不變,也就是說其遵守質量守恒原則,同時將泥石流中的流體與固體之間的相對運動忽略,將其看作單相流體[5]。將泥石流整個過程放在二維模型中,因此需要考慮x方向和y方向的質量守恒。另外,在泥石流的形成運動過程中,會有堆積和侵蝕的現象發生,并且堆積、侵蝕以及降雨都會對泥石流產生較大的影響,不容忽視。
根據上述影響因素,設定泥石流連續方程為:
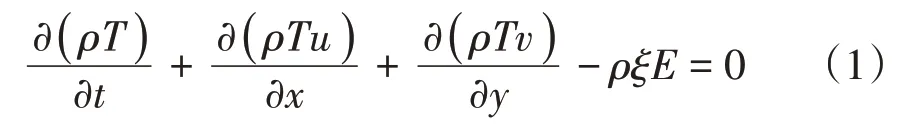
其中:ξ=,ρ為石流密度,單位為kg/m3;T為泥石流的厚度,單位為m;u,v分別為x方向與y方向的泥石流速度,單位為m/s;t為時間;ξ為修正系數;E為侵蝕率;Tb為河床的高度。
若將侵蝕與降雨的影響忽略,則公式為:
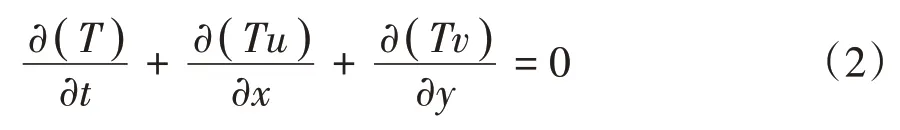
而在實際情況中,降雨量對泥石流的影響非常大,因此,本文在建立泥石流形成、運動控制方程時,增加了降雨量與流失量兩個項,則上述公式表示為:

其中:P為降雨的增加量;Q為降雨的流失量,單位為m/s。
假設泥石流在形成、運動過程中沒有間隙,也就是泥石流的運動是連續的,因此,泥石流形成運動過程中的動量守恒方程為:
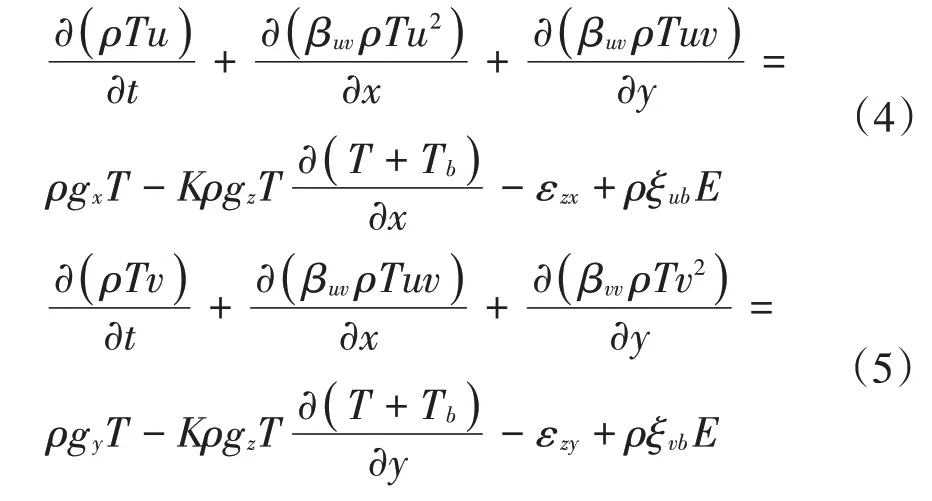
其中:β為動量分配系數;gx,gy,gz分別為在x,y,z軸上的重力分量;K為泥石流土的壓力系數;ε為泥石流的摩擦阻力。經過動量守恒方程的建立,可以減少模型計算的時間,使模型計算簡化,加快模型計算的效率。
采用Voellmy模型來對泥石流運動過程中遇到的抗剪應力進行計算,抗剪應力主要是摩擦力與阻力之和,其表達式為:

其中:σ為正應力;μ為摩擦系數;ε為泥石流的剪應力。
根據青藏高原泥石流的運動特征與運動模式,為了盡可能使計算變得簡潔高效,本文建立的泥石流形成運動過程控制方程將不考慮泥石流密度的變化、侵蝕的情況與動量分配系數,也就是將β設定為1,將控制方程進行簡化為
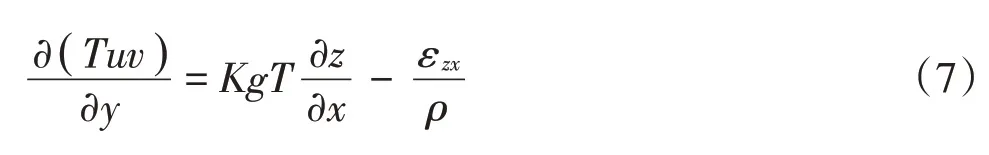
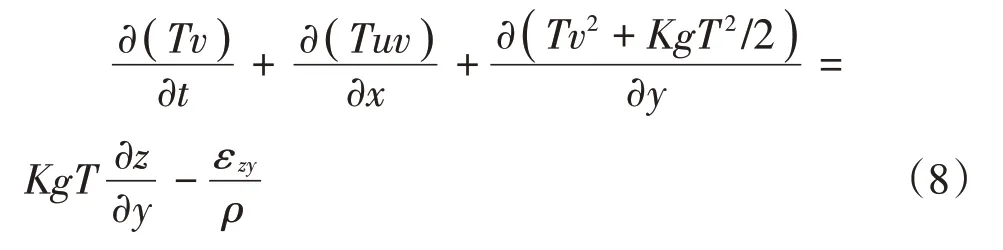
1.2 泥石流厚度與流速的計算
本文主要采用有限差分數值方法對控制方程進行計算,將上述公式轉化為矢量格式為:
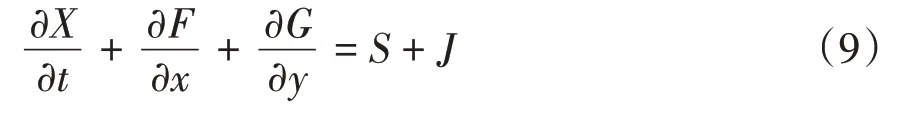
其中:X=
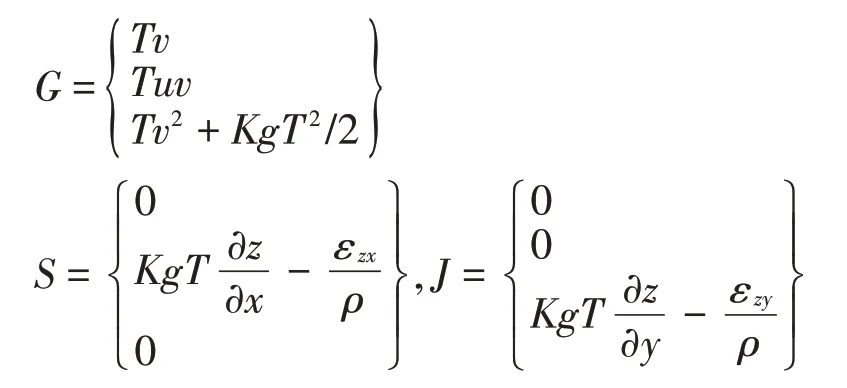
采用算子分裂方法將上述方程進行分解,將二維方程降為一維方程進行計算,其公式為:
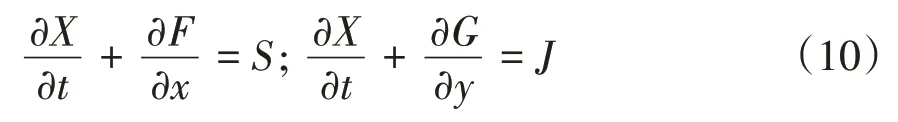
該方程具有穩定高效的特點,保證了計算的穩健性與有效性。
2 青藏高原泥石流形成運動過程模擬的實現
首先,對模型參數進行選取,主要包含兩部分內容,一是泥石流運動的初始條件,二是泥石流的運動條件。
初始條件主要包括泥石流的位置、厚度、模擬的計算范圍以及泥石流的初始位置與初始量。
通過DEM數字高程模型來對青藏高原的地形條件進行測量與輸入[6]。根據所得的地形情況,將易發生泥石流的位置進行切割,設定為研究區域,只針對這部分進行計算,其他部分不參與計算,這樣可以提升計算的效率。
對曾經發生的泥石流進行研究,發現青藏高原的物源條件主要來源于青藏高原坡面上風化的基巖,巖石經過風化會產生大量的泥土與石塊,還會帶有枯木等雜物,泥石流發生后,這些物源會產生堆積,若是再次發生泥石流,物源就會發生再次轉移[7]。因此,根據上述描述對初始條件進行設置,將平均物源厚度定義為0.01 m,在主泥石流運動方向內的物源厚度定義為0.1 m,在溝口處的物源厚度定義為1 m。
根據相關調查,泥石流的發生頻率和規模與降雨頻率和強度成正比例關系,因此,在進行泥石流形成運動模擬中對降雨頻率進行相應的設置,本文主要采用設計暴雨來對降雨強度進行表示。在研究區域內,設置兩處暴雨點,分別為A和B,A的權重為0.8,B的權重為0.2,根據模比系數計算相應的暴雨量[8]。
由于泥石流屬突發性災難,無法測量泥石流的容重。因此,本文根據研究區的地形條件以及泥石流易發程度量化評分標準,對模擬泥石流容重進行計算,得到泥石流的容重為1.9 t/m3。
本文采用的是Voellmy模型,該模型中包括兩個參數σ和μ,σ為湍流系數,μ為摩擦系數,通過模擬還原青藏高原泥石流的運動過程,將計算結果與真實情況進行對比分析,獲得泥石流的運動參數。
根據記載,青藏高原泥石流持續時間約為5 min,厚度為2~5 m,速度為6~8 m/s,隨著降雨量的增加,泥石流持續運動[9]。
通過實際情況設置相應的運動參數進行模擬,將μ范圍設置為0.1~0.5,σ范圍設置為10~90,其他參數一致。經過多次實驗,將得到的結果與實際情況進行比較,發現當μ為0.3,σ為10時,與實際情況最吻合。因此,將μ設定為0.3,σ設定為10。
然后,對青藏高原泥石流進行模擬。根據研究發現,青藏高原泥石流發生的周期大約為20 a。因此,本文對20年一遇的泥石流形成運動過程進行模擬。
該次模擬設定時間為5 min,分別對0.5 min、1 min、3 min與5 min的泥石流厚度分布、流速進行模擬計算。
2.1 泥石流厚度分布情況
當泥石流運動時間為0.5 min時,泥石流最大厚度為0.4 m,主要分布在主溝內,其他支溝的平均厚度為0.2 m,整體來看研究區內的泥石流厚度比較小,由于泥石流形成運動的時間較少,導致泥石流的運動有間隙;當泥石流運動時間為1 min時,泥石流最大厚度為0.54 m,主要分布在主溝內,其他支溝的平均厚度不足0.3 m,整體來看泥石流的運動呈現不連續的狀態;當泥石流運動時間為3 min時,泥石流最大厚度為1.6 m,主要分布在上游集水點,其他支溝的平均厚度不足0.7 m,并且處于支溝的下游部分;當泥石流運動時間為5 min時,泥石流最大厚度為2.4 m,主要分布在主溝下游,該部分屬于緩坡,容易產生堆積的現象。其他支溝的厚度不足0.6 m,大部分支溝沒有泥石流的堆積現象。
2.2 泥石流流速分布情況
整體來看,泥石流的流速是隨著時間的增加逐漸減小的。當泥石流運動時間為0.5 min時,流速為24 m/s,主要分布于支溝兩側的坡體上,由于坡度大,高度差較大,產生的重力也會隨之增加,泥石流的流速會相對較快,最大值可以達到20~24 m/s,到達支溝下游時,流速會減小到15 m/s,到達主溝后流速會再次減少為10 m/s,在主溝的中心部分流速為5 m/s;當泥石流運動時間為1 min時,泥石流會向主溝聚集,其流速約為5~10 m/s;當泥石流運動時間為3 min時,泥石流幾乎全部位于主溝,其流速約為15 m/s;當泥石流運動時間為5 min時,泥石流流速的最大值約為12 m/s[10]。
3 實驗結果與分析
為了保證本文構建的泥石流形成、運動模擬模型的有效性,設計實驗對其進行驗證。在實驗過程中,將泥石流作為實驗對象,主要是對其形成、運動過程進行模擬與分析。為了保證實驗過程與結果的準確性,使用構建的泥石流形成、運動模擬模型與傳統模擬模型進行比較,觀察實驗對比結果。在實驗過程中,將傳統模擬模型稱為對照組,構建的泥石流形成、運動模擬模型稱為實驗組。
3.1 數據準備
為了盡可能地保障實驗結果的準確性,對實驗過程中的參數進行相應的設置,本文采用不同的模擬模型對泥石流形成、運動過程進行模擬與分析,由于采用的模型不同,因此,在實驗過程中必須保證外部環境參數的一致。本文實驗參數設置結果如表1所示。

表1 實驗參數設置結果
3.2 實驗對比結果
在實驗過程中,由于采用的模擬模型不同,因此,本文利用ASO100軟件對實驗數據進行記錄與分析。主要通過模擬結果與實際情況的吻合度來驗證模擬模型的有效性。實驗對比結果如圖1、圖2所示。
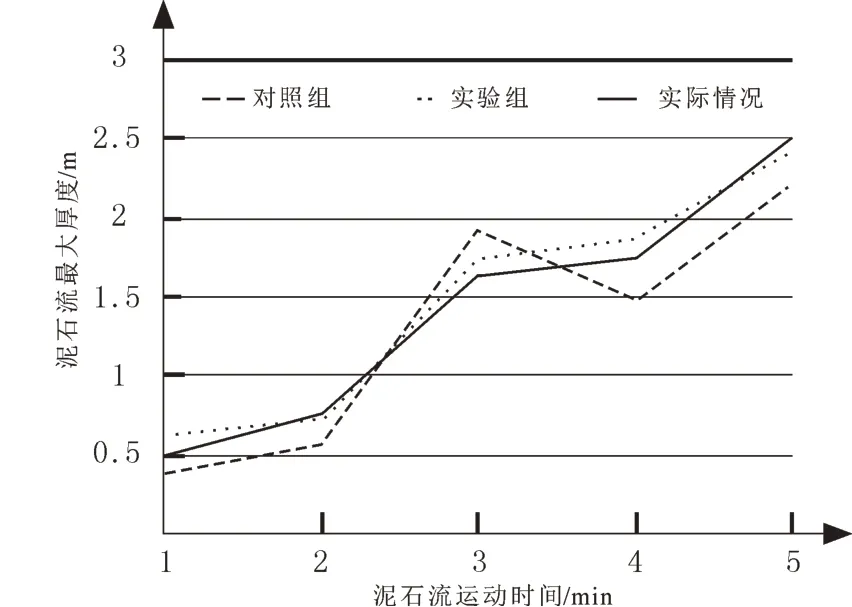
圖1 泥石流最大厚度實驗對比圖

圖2 泥石流最大流速實驗對比圖
由圖1可知,實驗組和對照組與實際情況的泥石流最大厚度的變化趨勢一致的,但是,實驗組與實際情況的吻合度更高。由圖2可以看出,實驗組與實際情況的泥石流最大流速的變化趨勢是一致的,而對照組的變化趨勢在運動時間3~4 min之內與實際情況是相反的,實際情況的變化趨勢是下降,而對照組的變化趨勢是上升,明顯與實際情況不吻合。因此,實驗組與實際情況吻合度更高。
綜上所述,實驗組與實際情況的吻合度遠遠高于對照組,說明本文構建的泥石流形成、運動模擬模型具備較高的有效性。
4 結語
本文主要構建了泥石流形成、運動模擬模型,對青藏高原泥石流的形成、運動過程進行模擬分析,實驗證明,該模型與實際情況的吻合度極高,可以為泥石流的預防與治理提供數據支撐。但是,吻合度還有提升的空間,需要進一步對其進行研究。

