改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟的競(jìng)合博弈研究

肖 旦,周永務(wù),范麗繁,謝國(guó)杰,謝 維

(1. 廣州大學(xué)工商管理學(xué)院，廣東 廣州 510006；2．華南理工大學(xué)工商管理學(xué)院，廣東 廣州 510641)

1 引言

在市場(chǎng)中，有一類特殊的商品，如果不考慮顧客對(duì)商品的需求，則隨著時(shí)間的流逝它們的重量得到增加、數(shù)量得到增長(zhǎng)、質(zhì)量得到改善，例如，養(yǎng)殖場(chǎng)中的生豬、雞、鴨等，魚塘中的魚、蝦等，花圃中的鮮花，果園中的水果，酒窖中的陳年好酒等，人們稱這種商品為改良品。由于某些農(nóng)產(chǎn)品具有易損耗的特征，而本文擬討論通過投資改良技術(shù)創(chuàng)新以提高改良率的改良品，因此，本文的改良品主要指以養(yǎng)殖戶為代表的供應(yīng)商所提供的產(chǎn)品。

近年來，越來越多的企業(yè)通過與政府部門、科研機(jī)構(gòu)的合作，對(duì)改良技術(shù)進(jìn)行創(chuàng)新，并在不同企業(yè)之間實(shí)現(xiàn)了改良技術(shù)的共享。例如，2017年5月，以內(nèi)蒙古鄂爾多斯市達(dá)旗農(nóng)牧業(yè)局的家畜改良工作站為主導(dǎo)，轄區(qū)內(nèi)的多家農(nóng)牧企業(yè)通過加大改良技術(shù)創(chuàng)新資金投入，加快了改良技術(shù)研發(fā)，推進(jìn)了肉羊品種的改良，帶動(dòng)了企業(yè)的增收。而江蘇省鹽城市濱海縣海洋林業(yè)漁業(yè)局則通過引進(jìn)優(yōu)質(zhì)漁業(yè)品種與養(yǎng)殖新技術(shù)，促進(jìn)全縣漁業(yè)養(yǎng)殖企業(yè)的快速高效發(fā)展。此外，眾多的養(yǎng)殖企業(yè)不僅共享了改良技術(shù)的創(chuàng)新成果，而且進(jìn)行改良品的聯(lián)合采購(gòu)。例如，2015年，6月步步高聯(lián)合生鮮采購(gòu)團(tuán)隊(duì)在越南與芹苣，大成，雄王等當(dāng)?shù)匾?guī)模最大的三個(gè)水產(chǎn)公司合作，成立越南巴沙魚直采基地。

雖然，改良技術(shù)共享與聯(lián)合采購(gòu)可能會(huì)降低改良品采購(gòu)聯(lián)盟的運(yùn)作成本，但是，是否選擇進(jìn)行改良技術(shù)創(chuàng)新，改良率提高到什么程度，是否進(jìn)行改良技術(shù)共享，形成改良技術(shù)共享與聯(lián)合采購(gòu)聯(lián)盟之后如何進(jìn)行運(yùn)作成本分?jǐn)偪梢员３制浞€(wěn)定性，是零售商進(jìn)行改良技術(shù)共享后改良品聯(lián)合采購(gòu)聯(lián)盟所需要解決的關(guān)鍵問題。目前，一方面已有一些學(xué)者針對(duì)改良品的采購(gòu)以及改良品供應(yīng)鏈的協(xié)調(diào)展開了積極的研究。例如，Hwang[1]首先在改良率小于(或大于)需求率的情況下，基于經(jīng)典的EOQ模型構(gòu)造了改良品的庫(kù)存控制模型。隨后，針對(duì)產(chǎn)品同時(shí)發(fā)生變質(zhì)與改良的現(xiàn)象，Mondal等[2]、Moon等[3]分別考慮了改良品的需求率與價(jià)格相關(guān)、零售商的資金具有時(shí)間價(jià)值等因素影響下改良品的庫(kù)存控制模型。Sana[4]在存儲(chǔ)容量有限的情況下，研究了改良品需求受到零售商銷售努力影響時(shí)進(jìn)行多物品聯(lián)合采購(gòu)的模型。而針對(duì)改良品供應(yīng)鏈的協(xié)調(diào)研究，國(guó)內(nèi)學(xué)者王勇等[5]首先采用數(shù)量折扣作為激勵(lì)機(jī)制，研究了一個(gè)供應(yīng)商和一個(gè)零售商構(gòu)成的改良品二級(jí)供應(yīng)鏈在批量對(duì)批量供應(yīng)模式假設(shè)下的協(xié)調(diào)問題，孫海雷等[6]則分析了如何利用價(jià)格折扣的激勵(lì)方式來實(shí)現(xiàn)對(duì)改良品二級(jí)供應(yīng)鏈的協(xié)作控制；張?jiān)曝S等[7]采用批量對(duì)批量的供應(yīng)模式，允許零售商缺貨且缺貨量全部拖后，比較了分散決策與集中決策下的供應(yīng)鏈最優(yōu)訂購(gòu)策略；張?jiān)曝S等[8]考慮在單一供應(yīng)商和單一零售商構(gòu)成的兩級(jí)改良品供應(yīng)鏈系統(tǒng)中，通過設(shè)計(jì)價(jià)格折扣和交易信用作為協(xié)調(diào)機(jī)制，研究了分散式供應(yīng)鏈下各成員企業(yè)的利潤(rùn)狀況及協(xié)調(diào)問題。

此外，與本文相關(guān)的另一方面的研究文獻(xiàn)為針對(duì)聯(lián)合采購(gòu)聯(lián)盟的運(yùn)作策略與穩(wěn)定性分析。首先，Meca等[9-11]分別在不同的情形下，采用EOQ模型討論了n個(gè)零售商的聯(lián)合訂貨問題；在此基礎(chǔ)上，Lin和Lin[12]、馮海榮等[13]討論了多個(gè)零售商聯(lián)合采購(gòu)易腐品的成本分?jǐn)倖栴}；Zhang[14]研究了多零售商共用一個(gè)中心倉(cāng)庫(kù)時(shí)的補(bǔ)貨策略；Chen[15]考慮了需求依賴價(jià)格時(shí)多個(gè)零售商進(jìn)行聯(lián)合采購(gòu)的問題；Fiestras-Janeiro等[16]研究了多個(gè)零售商可進(jìn)行合作運(yùn)輸時(shí)的聯(lián)合采購(gòu)問題；肖旦等[17]在隨機(jī)需求環(huán)境下分析了零售商聯(lián)合采購(gòu)與合并運(yùn)輸聯(lián)盟的穩(wěn)定性。而在制造商供應(yīng)商可提供數(shù)量折扣契約時(shí)，肖旦和周永務(wù)[18]討論了制造商與零售商進(jìn)行庫(kù)存合作時(shí)的運(yùn)作策略問題；肖旦等[19]采用最大一致集的概念，研究了橫向競(jìng)爭(zhēng)零售商聯(lián)合采購(gòu)聯(lián)盟的穩(wěn)定性。而關(guān)于改良品的聯(lián)合采購(gòu)模型，則僅有張?jiān)曝S等[20]在非瞬時(shí)補(bǔ)貨的情形下，討論了改良品聯(lián)合采購(gòu)聯(lián)盟的成本分?jǐn)倖栴}。

以上這些文獻(xiàn)對(duì)聯(lián)合采購(gòu)聯(lián)盟的穩(wěn)定性展開了一系列的分析，但是，他們并沒有考慮到聯(lián)合采購(gòu)聯(lián)盟成員間存在競(jìng)合博弈的情景。針對(duì)此問題，在知識(shí)共享網(wǎng)絡(luò)中，Bernstein等[21]首先對(duì)零售商間的競(jìng)合博弈策略展開了研究；隨后，肖旦等[22]在隨機(jī)需求下討論了庫(kù)存技術(shù)共享零售商聯(lián)合采購(gòu)聯(lián)盟的競(jìng)合博弈策略。但是，對(duì)于零售商間先各自進(jìn)行改良技術(shù)創(chuàng)新投資，然后共享改良技術(shù)并聯(lián)合采購(gòu)改良品的情形，上述文獻(xiàn)都尚未進(jìn)行研究。

本文采用逆推歸納法，針對(duì)確定的改良品市場(chǎng)需求，在既有改良技術(shù)投資競(jìng)爭(zhēng)又有改良技術(shù)共享合作的情形下，分析了改良品聯(lián)合采購(gòu)聯(lián)盟的運(yùn)作策略、成本分?jǐn)傄?guī)則與穩(wěn)定性。本文的具體結(jié)構(gòu)如下：首先，當(dāng)零售商各自進(jìn)行改良技術(shù)創(chuàng)新并在聯(lián)盟內(nèi)共享改良技術(shù)時(shí)，確定了改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟的運(yùn)作策略與總成本；隨后，給出了一種分配方案并證明該方案在改良技術(shù)共享下改良品聯(lián)合采購(gòu)合作博弈的核中；最后，得到了平均分?jǐn)偪偝杀镜姆桨笇⒉荒苁瓜到y(tǒng)的成本達(dá)到最低，但是，發(fā)現(xiàn)采用該合作博弈核的極點(diǎn)的成本分?jǐn)傄?guī)則，將可以使總成本降低至系統(tǒng)集中化決策時(shí)的水平。

2 模型的基本描述

本文基于經(jīng)典的EOQ模型，建立了改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成員間既有競(jìng)爭(zhēng)又有合作的競(jìng)合博弈模型。改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟中成員的決策順序如下：第一階段是競(jìng)爭(zhēng)階段。零售商各自對(duì)改良技術(shù)進(jìn)行改造升級(jí)，提高產(chǎn)品的改良率，在此階段零售商之間將在改良技術(shù)的投資水平上展開競(jìng)爭(zhēng)。第二階段為合作階段。此階段將分兩個(gè)步驟進(jìn)行，首先，聯(lián)盟內(nèi)成員將共享最先進(jìn)的改良技術(shù)；然后，零售商進(jìn)行改良品的聯(lián)合采購(gòu)。

圖1對(duì)上述零售商兩階段的決策順序進(jìn)行直觀的刻畫。首先，在競(jìng)爭(zhēng)階段的t1時(shí)刻，零售商們各自對(duì)改良技術(shù)進(jìn)行創(chuàng)新改造升級(jí)，提高改良率。其次，在合作階段的t2時(shí)刻，聯(lián)盟中的零售商進(jìn)行改良技術(shù)共享，統(tǒng)一提高聯(lián)盟內(nèi)零售商的改良水平；在合作階段的t3時(shí)刻，聯(lián)盟中的零售商將聯(lián)合采購(gòu)產(chǎn)品并銷售給終端消費(fèi)者。具體如如圖1所示。

圖1 改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟中零售商的決策順序

符號(hào)說明：

a：零售商每次訂購(gòu)改良品時(shí)的補(bǔ)貨啟動(dòng)費(fèi)用

c：零售商訂購(gòu)單位改良品的成本

ca：零售商改良單位改良品的成本

n：零售商的數(shù)量

N：N={1,2,...n}全體零售商的集合

Qi：零售商i(i=1,2,…n)的訂貨量

Di：零售商i(i=1,2,…n)面臨的市場(chǎng)需求率

hi：零售商i(i=1,2,…n)單位時(shí)間單位產(chǎn)品的持有成本

Ii(t)：零售商i(i=1,2,…n)在t時(shí)刻的庫(kù)存水平

Ti：零售商i(i=1,2,…n)獨(dú)立訂貨時(shí)的訂貨周期

TS：零售商聯(lián)盟S的統(tǒng)一訂貨周期

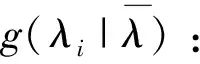
假設(shè)：

(1)供應(yīng)商對(duì)產(chǎn)品的補(bǔ)貨能力無限大，瞬時(shí)到貨，不允許缺貨。

(2)在改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟中各種信息是公共知識(shí)。

(3)改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟S中最高的改良率為λS，λS=maxi∈S{λi}。

3 改良技術(shù)共享改良品聯(lián)合采購(gòu)聯(lián)盟的運(yùn)作策略與成本

首先，單個(gè)零售商i的庫(kù)存水平在訂貨周期內(nèi)t時(shí)刻的庫(kù)存水平Ii(t)，將會(huì)由于產(chǎn)品改良而增加，同時(shí)由于市場(chǎng)需求而減少。故滿足微分方程：

由于Ii(Ti)=0，則易得，

因此，每次零售商i的訂貨批量為：

銷售改良品零售商i單位時(shí)間內(nèi)總成本為：

(1)

上式中的第一項(xiàng)為零售商i在單位時(shí)間內(nèi)訂購(gòu)改良品的啟動(dòng)費(fèi)用，第二項(xiàng)為在單位時(shí)間內(nèi)改良品的總采購(gòu)費(fèi)用，第三項(xiàng)為單位時(shí)間內(nèi)改良品的總持有成本和第四項(xiàng)為單位時(shí)間內(nèi)改良品的總改良成本。

但是，如果m(1≤m≤n)個(gè)銷售改良品的零售商形成改良技術(shù)共享的改良品聯(lián)合采購(gòu)聯(lián)盟S，該聯(lián)盟首先會(huì)共享最先進(jìn)的改良技術(shù)，即聯(lián)盟中的改良技術(shù)將會(huì)統(tǒng)一達(dá)到λS，其次，將會(huì)以統(tǒng)一的訂貨周期TS向同一供應(yīng)商進(jìn)行采購(gòu)。

改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成員的庫(kù)存水平在一個(gè)周期內(nèi)的變化規(guī)律將如圖2所示。即，在0時(shí)刻，聯(lián)盟中的每一個(gè)零售商將會(huì)根據(jù)自己的需求和聯(lián)盟的統(tǒng)一采購(gòu)周期向上游供應(yīng)商提出采購(gòu)量。隨著時(shí)間的流逝，經(jīng)過統(tǒng)一的采購(gòu)周期TS之后他們產(chǎn)品的庫(kù)存水平將變?yōu)?，并且本文假設(shè)產(chǎn)品可以瞬時(shí)到貨，因此，將在TS時(shí)刻開始新的聯(lián)合采購(gòu)活動(dòng)和銷售周期。

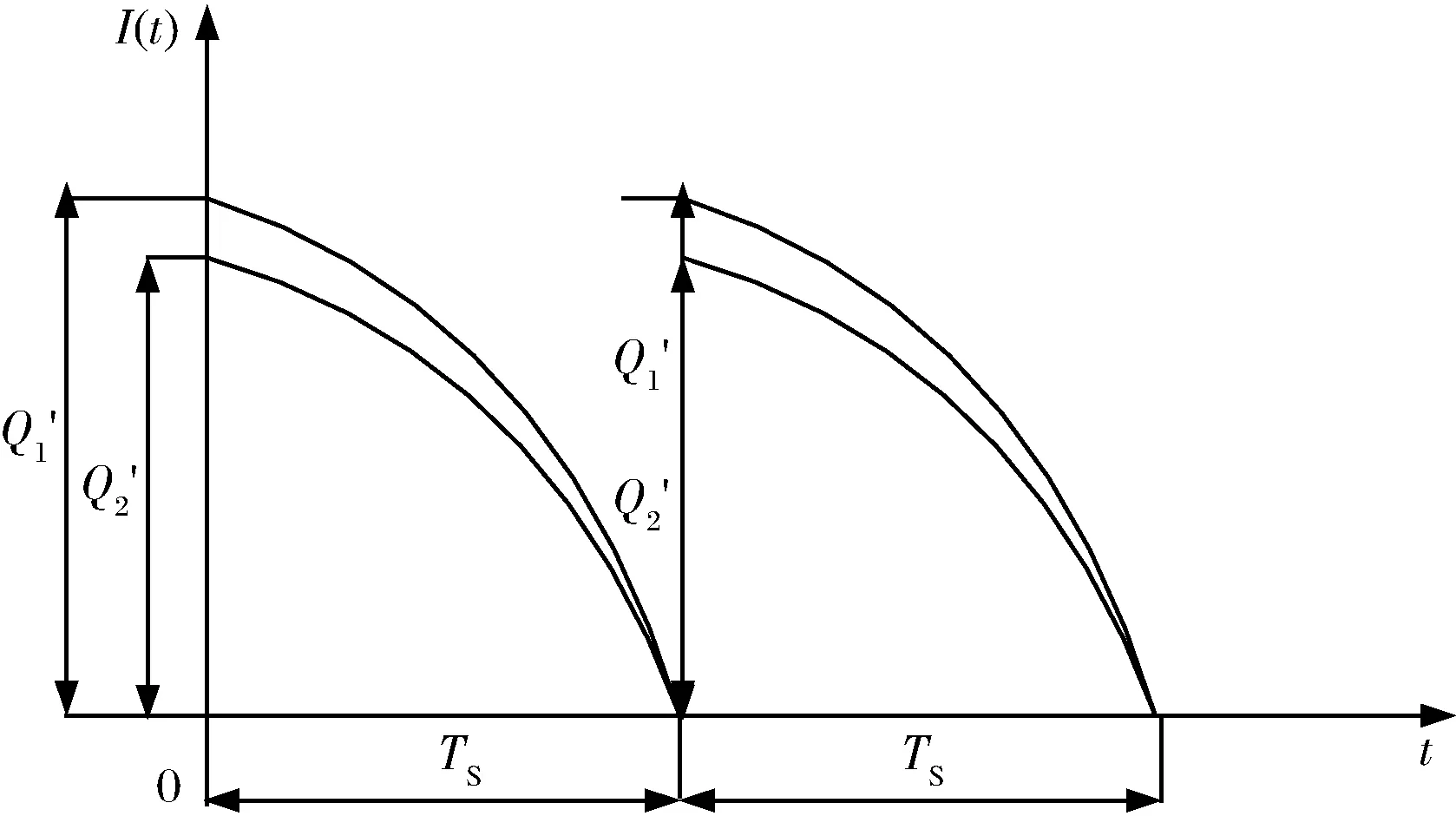
圖2 改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟中零售商的庫(kù)存水平變化

與(1)式類似，可以得到改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟在單位時(shí)間內(nèi)的總成本為：

(2)

對(duì)ACTC(TS)關(guān)于TS求二階導(dǎo)數(shù)，可知，

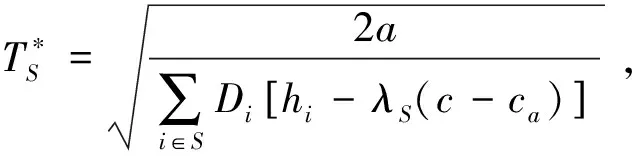
(3)

4 改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成本的分?jǐn)偡桨?/h2>

定理1改良技術(shù)共享下改良品聯(lián)合采購(gòu)情景所對(duì)應(yīng)的合作博弈具有次可加性的，即對(duì)于任意S,T?N，且S∩T=?，有f(S)+f(T)≥f(S∪T)。

證明：不妨假設(shè)任意的S,T?N，并且滿足S∩T=?，根據(jù)(N,f)的定義以及式(3)可知，

f(S∪T)=

λS∪T=max{λS,λT}，不妨設(shè)，λS≥λT，因此，λS∪T=λS，

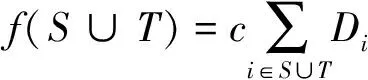
通過定理1可以知道，本文所定義的零售商在改良技術(shù)共享下改良品聯(lián)合采購(gòu)的合作行為將可以使所有參與合作零售商的總成本降低。此外，本文下面將通過合作博弈中核的概念，對(duì)其是否存在公平的成本分?jǐn)偡桨高M(jìn)行說明。首先，給出合作博弈核的定義如下。

定義 1：滿足如下條件的集合稱為合作博弈(N,f)的核：

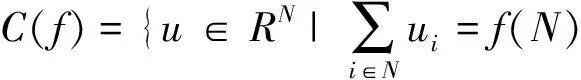
然后，為了方便刻畫公平合理成本分?jǐn)偡桨福疚膶⒃诟牧技夹g(shù)共享下改良品聯(lián)合采購(gòu)合作博弈的基礎(chǔ)上定義如下的合作博弈(N,v)。

下面將說明改良技術(shù)共享下改良品聯(lián)合采購(gòu)的合作博弈的核是非空的，即可以找到一種分配方案保持聯(lián)盟的穩(wěn)定性。為此本文先給出如下的定義。

定義3[22]：令π(N)是N的所有置換σ：N→N的集合，集合Pσ(i):={r∈N|σ-1(r)<σ-1(i)}含有關(guān)于置換σ的所有i的前繼。

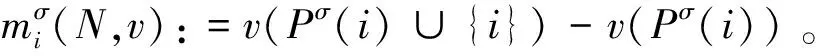
將聯(lián)合采購(gòu)聯(lián)盟成員的產(chǎn)品改良率進(jìn)行降序排列，并記為π(N,A)，因此，本文可定義如下的成本分?jǐn)傄?guī)則對(duì)改良技術(shù)共享下改良品聯(lián)合采購(gòu)大聯(lián)盟N的總成本進(jìn)行分?jǐn)偅?/p>

(4)

下面的定理2將說明這種成本分?jǐn)傄?guī)則對(duì)于改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟將是一種較為公平合理的分配方案，即該分配方案在其所對(duì)應(yīng)合作博弈的核中。證明過程請(qǐng)參見附錄。

定理2成本分?jǐn)傄?guī)則P(v)=(p1(v),p2(v),…,pn(v))是改良技術(shù)共享下改良品聯(lián)合采購(gòu)合作博弈(N,f)的一種核分配方案。

例1：假設(shè)市場(chǎng)中有兩個(gè)銷售改良品的零售商1和2，他們不僅進(jìn)行改良技術(shù)的投資競(jìng)爭(zhēng)，而且進(jìn)行技術(shù)共享和聯(lián)合采購(gòu)的合作。兩個(gè)零售商的參數(shù)具體如表1所示，通過計(jì)算可以知道f(1)=19.79，f(2)=25.83，f({1,2})=42.72。從而，可以得到p(v)=(16.89,25.83)∈C(f)。

表1 改良品聯(lián)合采購(gòu)聯(lián)盟中零售商的參數(shù)

5 改良技術(shù)創(chuàng)新時(shí)的投資博弈

本節(jié)將先討論改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟中零售商在集中決策下的改良技術(shù)創(chuàng)新投資博弈，然后指出平均分配的方案使零售商的改良技術(shù)創(chuàng)新的投資決策將不會(huì)達(dá)到系統(tǒng)最優(yōu)，最后給出了能使改良技術(shù)創(chuàng)新的投資達(dá)到系統(tǒng)最優(yōu)的成本分?jǐn)偡桨浮?/p>

首先，不妨設(shè)改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟對(duì)總成本的分?jǐn)偡桨笧閤(λ)=(x1(λ),…,xN(λ))∈C(f)，其中，xi(λ)為進(jìn)行改良技術(shù)共享與聯(lián)合采購(gòu)之后聯(lián)盟分?jǐn)偨o零售商i的成本。因此，零售商i的總成本φi(λ)為：

因此，改良技術(shù)共享下改良品聯(lián)合采購(gòu)大聯(lián)盟(即，所有零售商都參與所形成的聯(lián)盟)的總成本為：

上式中第二個(gè)等式成立是因?yàn)楹说亩x。

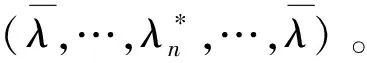
其次，下面我們將指出合作博弈階段關(guān)于總運(yùn)作成本的平均分配方案將不可能達(dá)到系統(tǒng)最低。

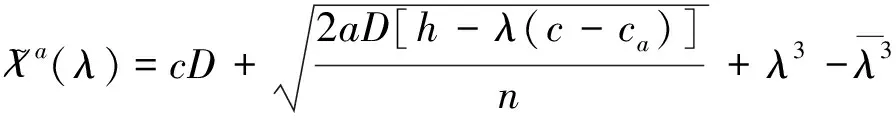
引理1. 如果給定其他零售商的改良技術(shù)創(chuàng)新投資，零售商i的最佳反應(yīng)策略為：

證明：為了證明引理1，我們需要證明如下幾個(gè)條件：

因此，可從如下幾個(gè)方面展開證明：

從而上式可以得到證明。

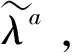
證明：

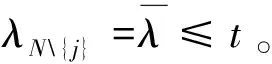
如果在平均分配規(guī)則下，則零售商的改良率將達(dá)不到系統(tǒng)最優(yōu)的改良率，從而導(dǎo)致其成本增加。

最后，與Bernstein等[21]的證明過程類似，本文指出當(dāng)合作階段選擇的分配方案為改良技術(shù)共享下改良品聯(lián)合采購(gòu)合作博弈的核的極點(diǎn)時(shí)，則可以達(dá)到使改良品聯(lián)合采購(gòu)聯(lián)盟達(dá)到系統(tǒng)最低的運(yùn)作成本。

定理5系統(tǒng)集中化決策時(shí)改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成員的最優(yōu)競(jìng)爭(zhēng)均衡策略，可以通過改良技術(shù)共享改良品聯(lián)合采購(gòu)合作博弈的核的極點(diǎn)得到。

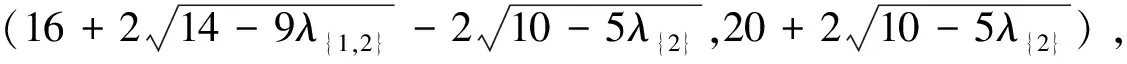
從而，知道在這種分配方案下λ{(lán)1,2}=λ{(lán)1}，因此，可以得到系統(tǒng)集中化決策時(shí)改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成員的最優(yōu)競(jìng)爭(zhēng)均衡策略為(0.59, 0.1)。

6 結(jié)語

改良品是市場(chǎng)中一類特殊的商品，它們的品質(zhì)會(huì)隨著時(shí)間的流逝得以改善，越來越多的企業(yè)通過技術(shù)創(chuàng)新提高改良率，并形成合作聯(lián)盟共享改良技術(shù)進(jìn)行聯(lián)合采購(gòu)。但是，形成改良技術(shù)共享與聯(lián)合采購(gòu)聯(lián)盟之后如何進(jìn)行運(yùn)作成本分?jǐn)偪梢员３制浞€(wěn)定性，是零售商進(jìn)行改良技術(shù)共享后改良品聯(lián)合采購(gòu)聯(lián)盟所需要解決的關(guān)鍵問題。本文基于經(jīng)典的EOQ模型，建立了改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟成員間既有競(jìng)爭(zhēng)又有合作的兩階段競(jìng)合博弈模型。首先，當(dāng)零售商各自進(jìn)行改良技術(shù)創(chuàng)新并在聯(lián)盟內(nèi)共享改良技術(shù)時(shí)，確定了改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟的運(yùn)作策略與總成本；隨后，給出了一種分配方案證明改良技術(shù)共享下改良品聯(lián)合采購(gòu)合作博弈的核是非空的；最后，指出平均分配方案所得到的改良率將低于集中化決策時(shí)零售商的最優(yōu)改良率，并指出在該合作博弈核的極點(diǎn)的成本分?jǐn)傄?guī)則下，此聯(lián)合采購(gòu)聯(lián)盟的總成本是最低的。

本文主要討論改良技術(shù)共享下改良品聯(lián)合采購(gòu)聯(lián)盟的競(jìng)合博弈策略，沒有考慮到隨機(jī)的改良率對(duì)采購(gòu)聯(lián)盟運(yùn)作策略的影響。總之，改良技術(shù)是否共享，改良技術(shù)共享之后運(yùn)作如何分?jǐn)偅瑢?duì)改良品聯(lián)合采購(gòu)聯(lián)盟的競(jìng)合博弈策略產(chǎn)生重要影響，這些是未來值得研究的重要問題。

附錄：

定理2 成本分?jǐn)傄?guī)則p(v)=(p1(v),p2(v),…,pn(v))是改良技術(shù)共享下改良品聯(lián)合采購(gòu)合作博弈(N,f)的一種核分配方案。

證明：

(1)與肖旦等[17]的證明過程相似，我們先考慮。

(2)含有改良率最高的零售商σ-1(1)，則有，