老師，為什么這方法失靈了？*
——2018年全國Ⅰ卷文科第21題的解題反思

福建省寧德市柘榮一中 (355300) 陳崇榮

2018年高考剛剛落下帷幕，做真題、研真題是老師、學生們的熱門話題，筆者也布置了一些真題給學生做并對其講解，在講評2018年全國卷Ⅰ文科第21題時引發了緊張而又驚喜的一幕.

題目(2018年全國卷Ⅰ文科第21題)已知函數f(x)=aex-lnx-1．

(1)設x=2是f(x)的極值點，求a的值，并求f(x)的單調區間；

1.課堂片段簡錄

針對第二問，平淡的課堂引起了波瀾.

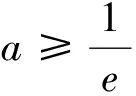
師：同學們，此題簡單嗎？

生：(多數學生)簡單.但是不會做.

于是筆者請學生回答思維受困的原因.

沒有想到學生拋出了這樣的問題,這是課前沒有預設的情況.此時此刻,全班同學的眼光齊聚在筆者身上,同時議論紛紛.沒有辦法,弦已開弓,只好接招了.

師：大家安靜,我們請這位同學說說他的解法.

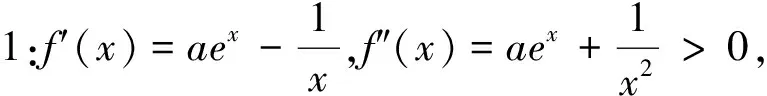
當x從右邊無限趨近于0時，f′(x)<0；當x無限趨近于+∞時，f′(x)>0.

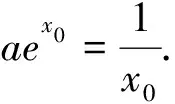
師：請坐.這位同學把問題轉化為了我們熟悉的恒成立問題,而且也通過“設而不求”的方法求出了函數的最小值f(x)min=aex0-lnx0-1，很好.那么大家想想如何證明函數的最小值會大于0呢？

(有的在沉默思考中，有的在和同桌小聲交流著，教師也借此機會在思考著……)

師：回答太好了，同學們，掌聲鼓勵！

掌聲未熄，另外一名學生也站起來了……

生3：老師，我也是轉化為恒成立問題，但不是去求f(x)的最小值，而是分離了參數a，也是解不出來，為什么呢？

看來一波剛平，一波又襲.但此時的我，卻淡定了許多.

師：那請展示你的解答過程.

師：同學們，大家一起思考，看能否幫助這位同學回答這問題呢?

(思考2分鐘后，有同學舉手了)

師：太棒了.同學們，剛才這幾位同學的思考方向及解決辦法非常的好，其實就是利用了解決恒成立問題的通性通法---最值法和參數分離法，你們說，此方法在此題失靈了嗎？

眾學生：(高興的大聲回答)沒有！

師：同學們，還有其他方法嗎？

師：(學生沉默)老師剛剛在你們思考的同時也想到了另外一種方法.(教師引導，師生一起合作完成以下解題方法)

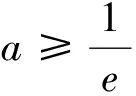
2.解題反思

每次試卷講評后，部分學生都懊惱：那么簡單的方法考試的時候為什么就想不到呢？自然想法無法通達，通性通法難以湊效.原因在于學生對相關問題的理解浮于表面、流于形式，平時訓練采用“題型+技巧”的題海戰術，卻沒有跳出題海，不能理清楚問題的邏輯，更談不上透過現象揭示本質，領會數學思想和方法內涵，以至于解題時被命題人牽著鼻子走，撞到南墻不回頭.

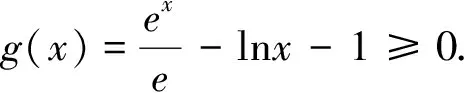
3.學好數學四步曲

學好數學第一步是弄“懂”.“懂”是指對數學概念、公式、法則的產生、背景一清二楚，對概念的內涵外延、變型要理解和掌握.

學好數學第二步是弄“會”.“懂”了不一定“會”，懂和會是不一樣的層次.有些學生上課聽懂了，但作業、考試還是不會做，原因有兩種：一種是很多學生都是假懂，似懂非懂；另外一種是從懂到會還有一段路程要走，要經歷“套用”--“變用”---“活用”三個階段.“套用”，指直接套用公式、法則、解題方法；“變用”指能靈活使用公式、法則的變型，包括正用，逆用，變形用;“活用”是在陌生情景也能創造條件轉化為我們熟悉的模型、情景,從而套用公式、法則或是解題方法等.經歷了這三個階段，這才叫“會”.

學好數學第三步是做“對”.“會”了，不一定“對”，即“會”而不“對”.因為有時自己感覺“會”做了，其實是“霧里看花”，假“會”，數據改一改，條件變一變立馬就不會了.萬變不離其宗.真正做到“會”，就要在“宗”字上下功夫.變式訓練，組題訓練，題海訓練目的就是讓學生“沉入水底”，認“宗”悟“宗”，真正理解知識的本質，感悟知識所蘊含的數學基本思想.

學好數學第四步是“快”.“天下武功，無堅不破，唯快不破”.“對”了，不一定“快”.熟能生巧，熟則快捷.要做到“見題生法，見招拆招”，一是要全面掌握各個模塊知識點，二是要熟悉各種解題思路和方法，還要有扎實的基本功以及敏捷、嚴謹的思維品質.