幾道高考壓軸題的自然解法與解題思考

福建省閩清教師進修學校 (350800) 黃如炎

導數與函數綜合題大多作為高考壓軸題，主要考查理性思維和創新意識.對導數與函數綜合題學生思路迷茫，一籌莫展，在考試中幾乎是空白題.高考命題組給出的標準解答具有抽象、嚴謹、精練、規范的特點，體現了數學的理性思維，很有數學味，但由于沒有給出解題的思維過程(連圖形都沒有)，使人很難領悟標準解答，對直接給出的某些結論，學生感到莫名其妙，如墜煙海，不利于學生思維的培養和素養的發展．

“數學是自然的，數學是清楚的”[1]，因此數學解題應是清晰明理的！本文對2018年高考幾道典型的函數與導數壓軸題，探析不同于命題組標準解答的自然、明快的解法，從中感悟解決函數與導數綜合問題的基本通徑和主要對策．

1 試題探析

題1 (2018年高考全國Ⅲ卷理科第21題)已知函數f(x)=(2+x+ax2)ln(1+x)-2x．(1)若a=0，證明：當-10時，f(x)>0；(2)若x=0為f(x)的極大值點，求a．

第(1)步略，第(2)步探析如下．

探析:f′(x)=(1+2ax)ln(1+x)+

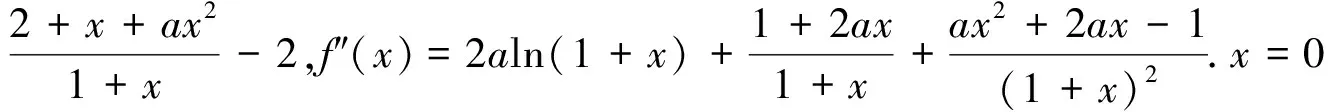
圖1

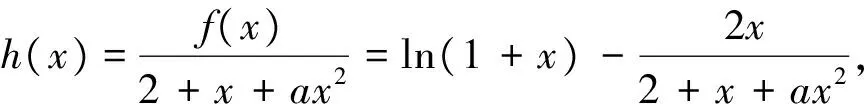
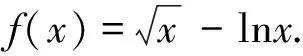
第(Ⅰ)步略，第(Ⅱ)步解析如下．

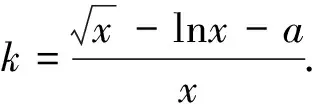
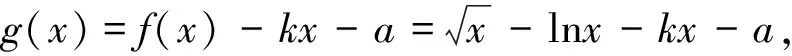
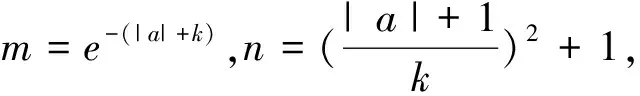
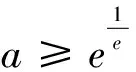
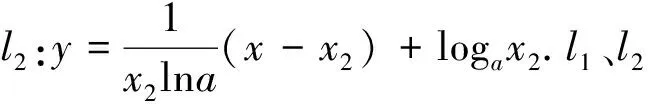
標解評析:命題組的標解是通過研究函數u′(x)的零點、單調性和符號，找到函數u(x)最大值u(x0)，再證u(x0)≥0，還用到第(Ⅰ)步的結論．本解法不用探求u(x)最大值，無需前問鋪墊，通過特殊點的精準驗證和函數式的靈活放縮，達到優化解題思維，提高解題品質．

題4 (2018年高考全國Ⅱ卷理科第21題) 已知函數f(x)=ex-ax2.

(1)若a=1，證明：當x≥0時，f(x)≥1；

(2)若f(x)在(0，+∞)只有一個零點，求a．

第(1)略，第(2)步解析如下．

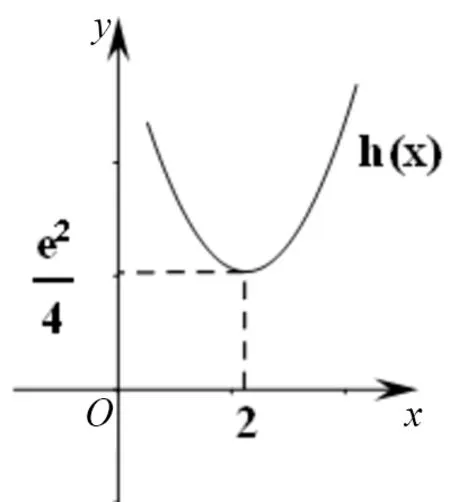
圖2

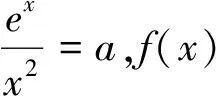
標解評析:命題組的標解是根據f(x)=ex-ax2=e2(1-ax2e-x)，把f(x)在(0，+∞)只有一個零點等價轉化為h(x)=1-ax2e-x在(0，+∞)只有一個零點．在尋找h(x)零點存在區間時，利用不等式ex>x2進行放縮，較難想到．

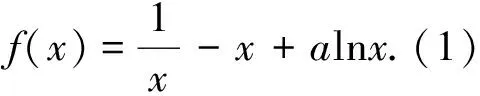
第(1)步略，第(2)步探析如下.

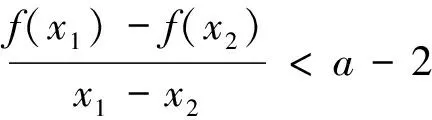
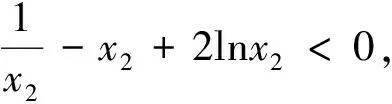
2.解題思考

《普通高中數學課程標準》(2017年版)指出：“直觀想象是發現和提出問題、分析和解決問題的重要手段，是探索和形成論證思路、進行數學推理、構建抽象結構的思維基礎”[2].函數圖像刻畫了函數的性質，圖像為抽象的推理增添了形象支持，在茫然的思路中，圖像指引著推理的方向．因此研究函數與導數綜合問題要順應學生從形象思維到抽象思維的認知過程，通過直觀想象，把對“形”的感知轉化為對“數”的表達．求解函數與導數綜合問題的基本通徑為：

(1)求導，確定函數單調區間．

(2)作圖，根據函數單調性和關鍵點(如定義域區間端點、坐標軸交點、極值點等)作出函數圖像．

(3)推證，依托圖像確定推理證明的方向．

函數與導數綜合題常涉及到零點存在問題，導函數零點不可求問題，不等式問題和含參問題，主要解決對策有：

(1)對函數零點存在問題，關鍵在零點兩側探求實數m、n(可以是一個具體的數、式或區間)，使f(n)f(m)<0．

①特值驗證：根據函數式的特征，取特殊自變量m，驗證是否滿足f(m)>0(或f(m)<0)．

②解不等式：當不等式f(x)>0(或f(x)<0)可解時，可直接通過解不等式求出滿足f(m)>0(或f(m)<0)的實數m．

③放縮化歸：當f(x)較復雜時，可將f(x)放縮為簡單的函數g(x)，使f(x)>g(x)(或f(x)0(或g(m)<0)，則f(m)>g(m)>0(或f(m)

為便于放縮，可根據函數圖像和解析式特征，在某特定范圍內進行放縮．對含有指、對數函數的要注意運用重要不等式ex≥x+1,lnx≤x-1進行放縮．還要注意能否利用前問結論進行放縮．

(2)對導函數零點不可求問題，可再次求導，通過高一階導函數的零點研究函數性質．若多次求導后的函數零點仍不可求，可將函數放縮或化歸轉化為簡單的函數求解．

(3)對不等式問題，要先構建相應函數再運用導數求解(證)．

(4)對含參問題，要注意變量分離和分類討論的緣由．

教學中要講道理，多體悟，力求解題思路的自然形成.教師要啟迪學生利用直觀想象與推理論證相結合的方法，沿著求導→作圖→推證的基本路徑，通過特值驗證或放縮化歸探求函數零點存在區間；通過再次求導或放縮化歸解決導函數零點不可求問題；通過構建函數和求導求證(解)不等式；通過分類討論或變量分離求解含參問題．