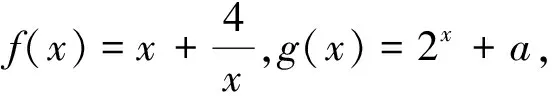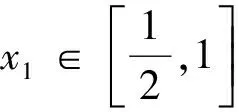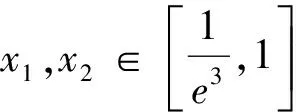處理雙變量函數問題的五種方法
河南大學數學與統計學院 (475001) 盧 陽 張蒙蒙
在近年來的函數綜合題中,常常出現兩個在某個范圍內都可以隨意變化的量,即雙變量函數問題.這類問題學生常常由于不知選擇哪個自變量作為研究對象而導致思路無法繼續.為此,本文歸納梳理解決這類問題的思想和方法,對同學們攻克函數綜合問題將有所幫助.
一、變量歸一,消元構造法
雙變量問題含有兩個變量,很自然的想法便是消去一個變量,變成一元函數問題.
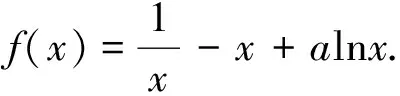
(1)討論f(x)的單調性;
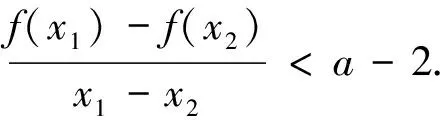

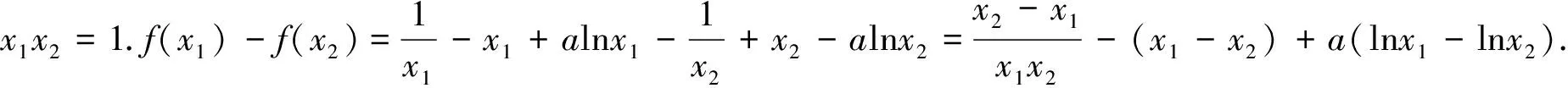

評注:該題兩元之間存在關系,故可消去其中一個變量,變成一元函數解決,該類問題近幾年經常出現,如2016年課標全國卷Ⅱ第21題做法和此題非常相似,難點在于找到各元之間的關系,讀者可以對比歸納.
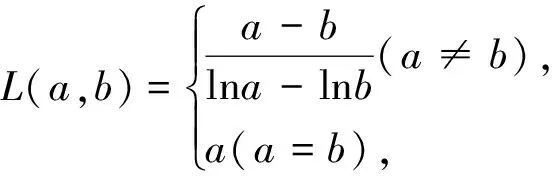
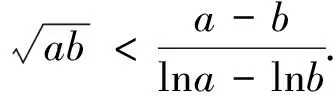
評注:由上證不等式可以很快得出例1的答案.對數平均不等式的證明方法具有代表意義,很多問題都需要把雙變量所代表的運算式看成整體去進行消元.
例3 已知函數f(x)=aex+b在(0,f(0))處切線為x-y+1=0.
(1)求f(x)的解析式;
(2)設A(m,f(m)),B(n,f(n)),m 設h(t)=et-t-1,h′(t)=et-1>0,t>0.即h(t)在(0,+∞)上單調遞增,所以h(t)>h(0)=0,故t 小結:例1、例2、例3都是通過消元去解決問題.不同的是,例1根據題目條件可以直接消去其中一個變量;例2,例3需要創造條件,把雙變量看成一個整體,我們稱為“變量歸一”思想. 例3的方法帶有一定技巧性,有些學生不易想到,觀察到兩變量之間是相互獨立的,可以“矮子里面挑將軍”,選擇其中一個變量當成主變量,視其他變量為參數進行討論. 對例3再采用“指定主元法”進行解決,把n當成主元,把m當成參數. 分析:a,b地位一樣,直接操作,不知“力往何處使”.不妨將a當成主元,著重使力. 解:先證右邊,即證alna-blnb>(a-b)(lnb+1).以a為主元,設h(a)=alna-(lnb+1)a-blnb+blnb+b,a∈(0,b).即h(a)=alna-(lnb+1)a+b,h′(a)=lna-lnb<0.所以h(a)在(0,b)上單調遞減,則h(a)>h(b)=0.所以當a∈(0,b)時,alna-blnb>(a-b)(lnb+1).左邊同理可證. 小結:指定主元法在雙變量問題中經常使用,前提是兩個變量之間“無牽無掛”.如例2也可以用指定主元法解決,有興趣的讀者可以試做.但若兩變量之間有聯系,如例1,那么便不能指定其中一個變量為主元進行討論. 雙變量問題中含有兩個變量,有時按照常規思維對兩個變量進行區分主次,往往會陷入困境.此時若變換主元,反客為主,會有柳暗花明的感覺. 例5 (2017天津預賽題)實數a,b滿足|a|≤1,|a+b|≤1,求(a+1)(b+1)的取值范圍. 分析:此題a,b關系不好直接表達出來.若設t=a+b,則可將b消去. 評注:此題若把a看成主元,則是關于a的二次函數,需要對對稱軸的位置進行討論.轉變視角之后變成關于t的一次函數,則簡化此題. 小結:從上述兩例可以看出若主元選擇得當,將會降低思維難度,簡化解題過程,主元變換最大的好處就是把復雜函數變成簡單函數.另外,主元變換蘊含著轉化與化歸思想,體現了和諧統一,普遍聯系的哲學觀點,使用得當,往往會使我們另眼看題. 雙變量問題多為不等式問題,而不等式的證明常常需要利用函數單調性來處理.因此,單調性構造法顯得尤為重要. 例7 已知函數f(x)=(x-1)ex+ax2有兩個零點.(1)求a的取值范圍;(2)設x1,x2是f(x)的兩個零點,證明x1+x2<0. 分析:第(1)小題一般采用單調性的討論來判斷零點個數,答案也是這么給出的.但如果利用函數與方程思想將零點問題變成兩函數交點問題便能化繁為簡;第(2)小題是極值點偏移問題,需要將兩變量變到同一單調區間,再利用單調性證明. 解:(1)見分析,a>0.(2)不妨設x1 評注:極值點偏移問題從2009年開始出現,到2016年再一次出現在全國卷上,屬于難題.最主要的難點在于需要將x1,x2變到同一單調區間,再聯系單調性進行證明.在證明過程中,還有一個難點在于如何將x1,x2和a三個變量進行消元變成一個變量,這里需要用到方法一的“變量歸一,消元構造法.” (1)求f(x)的單調區間; (2)存在x1,x2∈(1,+∞)且x1≠x2,使 |f(x1)-f(x2)|≥k|lnx1-lnx2|成立,求k的取值范圍. 小結:以上兩例都是通過等價轉化為函數單調性問題加以解決.另外,例8也可以用指定主元法解決.讀者可以嘗試. 分析:題意實際上是想說明無論f(x1)怎么取值,都有g(x2)比它大,也即f(x)max≤g(x)max. 評注:實際教學中很多學生對“任意、存在”問題難以理解,筆者將這類問題形象的表示為“孫悟空與如來佛”的故事.如例9,把f(x)看成孫悟空,把g(x)看成如來佛,題目可以表示為“無論孫悟空在M時期法術有多強,在N時期都存在某種狀態的如來佛可以擊敗他”,即M時期孫悟空法術最大值≤N時期的如來佛法術最大值,也即f(x)max≤ g(x)max. 總結:函數題中的雙變量問題是近年來高考中的“寵兒”,題型多樣,方法多變,對思維能力和運算能力要求較高.在學習這類問題時需要通過練習熟悉題型,更重要的是領悟每種方法背后的思想,從而進行歸納整理.筆者給出處理這類問題的五種常見方法與其中蘊含的數學思想,旨在拋磚引玉,希望引起讀者思考.
二、委以重任,指定主元法

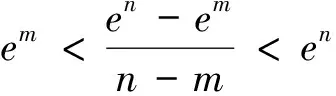
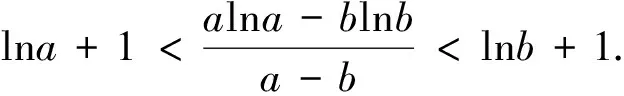
三、反客為主,變換主元法
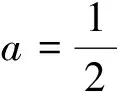
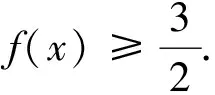


四、利用性質,單調性構造法
五、理清題意,轉化為最值問題法