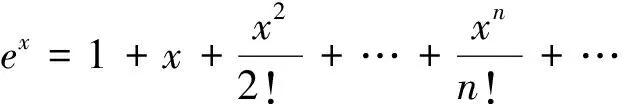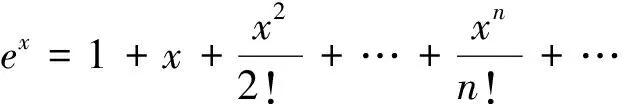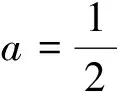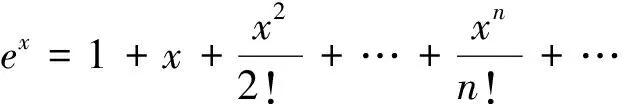泰勒公式在高考試題中的命制分析

福建省泉州市第七中學 (362000) 彭耿鈴

近年來，國家高考試卷中帶有高等數學背景的壓軸題經常出現，這主要源于兩個因素：一是高考試題要考查學生的創新學習能力，這就需要有一個比較公平又有區分度的知識背景，而高等數學的一些內容可以通過初等數學的方法和手段解決，是考查學生進一步學習高等數學潛能的良好素材；二是高考命題組成員為大學老師，他們在命題時受自身研究高數背景的影響，因此一些具有高等數學傾向的問題逐步走進高考.事實上高等數學中“泰勒公式”經常通過改編而成為高考試題、各地模擬質檢的壓軸題目，從而考查學生的數學學科素養.本文特精選幾道以“泰勒公式”為背景的高考壓軸題進行分析，希望讀者有所啟示，并預祝能在高考中勝出！

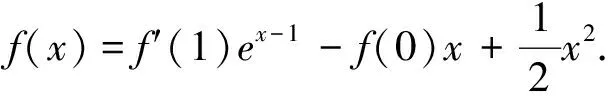
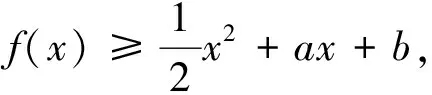
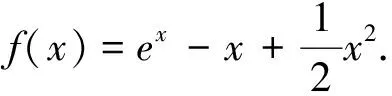
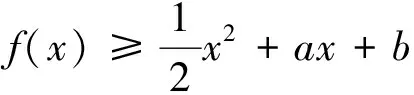
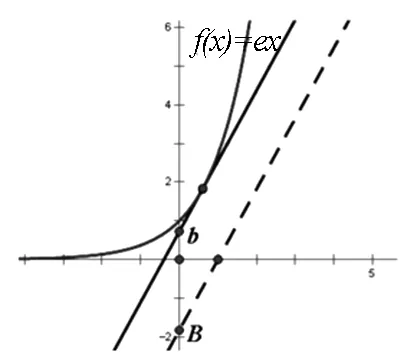
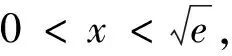
盡管這道高考試題的設計來源于高等數學的“泰勒公式”，但命題者提供的方法最終還是中學所學的導數知識加以解決，但是我們如果利用“泰勒公式”來解題，則解題的思維會更加流暢、更容易接近問題的本質.因此老師們在日常的教學中，應引導學生經歷用不同的思想、方法去探究、解決數學本質問題的來龍去脈，培養學生更自然的解題策略，使得解答更臻于完美，真正地提高學生的解題能力！以下是幾道以“泰勒公式”為背景的高考同類變式題.

變式1 (2014年全國新課標Ⅱ理科21題)設函數f(x)=ex-e-x-2x.

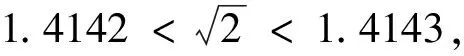
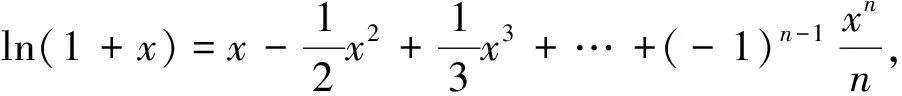
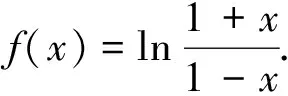
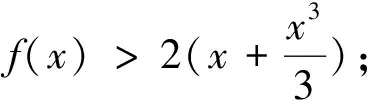
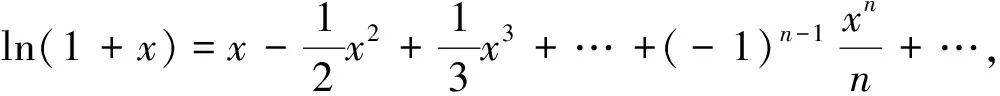
變式3 (2014年福建高考理科20題)已知函數f(x)=ex-ax(a為常數)的圖像與y軸交于點A，曲線y=f(x)在點A處的切線斜率為-1.(Ⅰ)求a的值及函數f(x)的極值；(Ⅱ)證明：當x>0時，x2

變式5 (2010年課標高考全國卷理科21題)設函數f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的單調區間；(Ⅱ)當x≥0時，f(x)≥0，求a的取值范圍.

變式6 (2010年課標高考全國卷文科21題)設函數f(x)=x(ex-1)-ax2.

作為中學老師和對數學特感興趣又學有余力的優秀學生，我們應該自覺主動接觸一些基本的高等數學知識和方法，尤其是高等數學的“泰勒展開式，極限方法的應用，不動點問題，函數圖像的凸性，中值定理，二階常系數線性差分方程”等與中學數學有著千絲萬縷關系的經典問題，才能胸有成竹，居高臨下，決勝于高考！