關(guān)鍵卡在哪兒？
——一道中考數(shù)學(xué)題的命題與解法

山東省日照市五蓮縣教學(xué)研究室 王金鳳

一道命題巧妙、立意獨特的中考試題能夠更加準(zhǔn)確地檢測出學(xué)生的真實水平，更好地發(fā)揮升學(xué)篩選的作用，同時還可以對教師的數(shù)學(xué)教學(xué)起到引導(dǎo)作用。重慶市2015年數(shù)學(xué)中考試卷第25題給我們的感覺是第三小題的圖形很復(fù)雜，證明起來難度較大，那么如何才能降低題目的解答難度，解題的關(guān)鍵在哪里？這是本文嘗試探討的問題。

一、試題介紹

（2）試證：HP =HF。

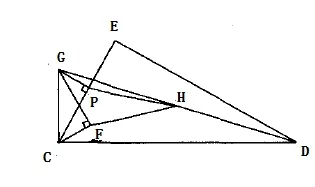
圖1

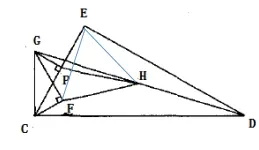
圖2

二、分析與解答

問題（1）中，已知∠CED為直角，∠DCE=60°，根據(jù)勾股定理可知CD=2CE，而CE=，因此，CD=，DG=。問題（2）比問題（1）難度稍大，需要添加一條輔助線，如圖3所示，并進(jìn)行簡單推理，考查的是基本技能。

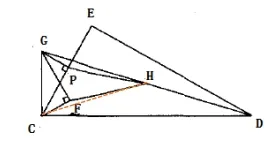
圖3

如圖3，添加輔助線CH，GP=CF，GH=CH，因為∠FCH=∠FCD-∠HCD=30°-∠HCD；∠HGP=∠HGC-∠PGC=∠HGC-60°=（90°-∠HDC）-60°=30°-∠HDC，可得∠HGC=∠HGP，△PGH≌△FCH，證得HP =HF。

問題（3）保留了問題（2）的線段，少了點P是CE中點的條件，屬于開放式命題，考查的是綜合能力，難度較大。

證明：如圖4所示，取CD中點K，連接EK，HK，在直角三角形△中，CG =2CF，HK是△CGD的中位線，因此，CG =2HK，可知△為等邊三角形，故CE=EK，又因為∠ECF=∠DCE=30°，∠EKH=∠CKH－∠EKC=30°，可知△ECF≌△EKH，所以∠CEF=∠KEH，∠CEF+∠FEK=∠KEH+∠FEK=60°，可得△FEH為等邊三角形。

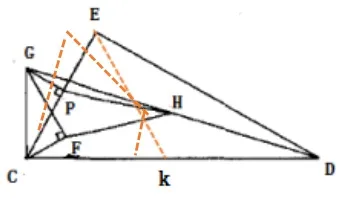
圖4

該方法充分利用兩直角三角形的中點構(gòu)成中線和中位線，并構(gòu)造全等三角形，從而聯(lián)想到幾何變換，引出了上述的證明思路：添加輔助線，通過證明△FEH有兩條邊相等，再證明其中一個角為60°，從而證明其為等邊三角形。從幾何變換角度來說，如圖4所示，證明了一對全等三角形，相當(dāng)于△EFC繞點E旋轉(zhuǎn)得到△EHK。通過圖4的證明方面，我們可以看出圖2有瑕疵。

綜合性幾何題目為了呈現(xiàn)各個題目之間的關(guān)聯(lián)，體現(xiàn)從易到難的命題原則，通常需要組合多個知識點以及圖形拼接、疊加等。……