一二維分片勢阱問題的譜元法高效求解

北京計算科學研究中心 劉 焱

薛定諤方程是數學與物理中經典的問題，它描述了波函數量子行為，在流體力學、固體物理、電磁學、量子化學、凝聚態物理及光學等廣泛領域內有著重要應用。

無序勢阱定態薛定諤方程的波函數會出現高度局域化現象，該現象在相關物理領域中稱為安德森局域化。安德森局域化的研究已經有五十年以上的歷史，但依然有很多相對開放的研究課題。

2016年，DouglasN.Arnold提出，在無序勢阱的條件下，薛定諤方程的特征值及特征函數局域化區域，可以由求解相應的源問題進行預測，并給出了理論上的部分證明。Arnold以分片常數隨機勢阱模擬無序勢阱，利用三次有限元方法完成了一維和二維的數值算例，得到了經驗性的結論，但數值結果的精度低，規模小。

考慮單位方形區域內，零邊界條件下簡化的薛定諤方程及其對應的源問題：

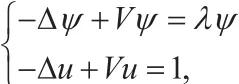
其中，V為勢阱函數。

逼近無序勢阱要求使用大規模分片勢阱V，有限元方法難以完成對大規模相應的特征值問題及源問題的數值求解。針對大規模分片勢阱薛定諤方程及源問題，本文提出了高效的譜元法數值格式，并設計快速算法，得到了一種低計算量、高效且高精度的數值方法。利用該高效數值方法，本文在同等精度要求下，完成了更大規模的數值算例求解。

本文結構主要分為兩個部分：第一部分，我們基于勢阱分布完成了網格剖分，發展譜元法提出了數值格式，設計了相應的快速算法。第二部分，在一維及二維的數值實驗中，我們首先檢驗了譜元法的有效性及相對有限元的優越性，然后驗證了安德森局域化現象，最后完成了對特征解預測理論的高精度數值研究。

一、無序勢阱問題的譜元法

源問題預測特征解的部分理論支持參見DoulasN.Arnold所著的相關文獻，因此本節僅描述數值方法。

首先，對無序勢阱使用分片常數隨機勢阱進行逼近。不失一般性，對一維單位區間[0，1]進行均勻剖分，多維區域由一維區域分解張量形成。使用在每個子區域內取隨機常數的分片常數隨機勢阱來模擬無序勢阱。

源問題與特征值問題的變分形式及逼近格式不再贅述，重點描述基函數的選取。

參考沈捷等人的著作[5]中節4.1.2的內容，引入在[-1，1]上的基函數，這組基函數滿足剛度矩陣為單位矩陣，質量矩陣為三帶寬五對角矩陣。在此基礎上進一步優化，于是得到一組新的基函數，其對應的質量矩陣與剛度矩陣均為對角陣。結合有限元對區域選擇的靈活性與譜方法的高次數高精度特性，生成譜元法基函數，進而拼接得到一維全局譜元法基函數，而二維逼近空間的基函數即為一維基函數的張量積。

得到基函數與逼近空間后，將問題轉化為離散問題線性系統。

以二維情況源問題對應的線性方程組為例，說明譜元法對應的快速算法的核心內容。

基于Schur補的思想，通過一個恰當的置換矩陣，我們將線性方程組重排為：

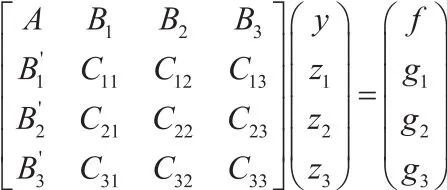
其中，矩陣塊A為對角矩陣，其他矩陣塊為稀疏矩陣。利用線性有限元，分別在xy兩個方向及單獨一個方向替換譜元法，我們可以得到z1，z2，z3的低精度近似解。利用矩陣塊A我們可以得到y的近似解。于是我們得到線性方程組的預條件子，結合共軛梯度法，我們便有高效的迭代求解算法。

二、數值實驗

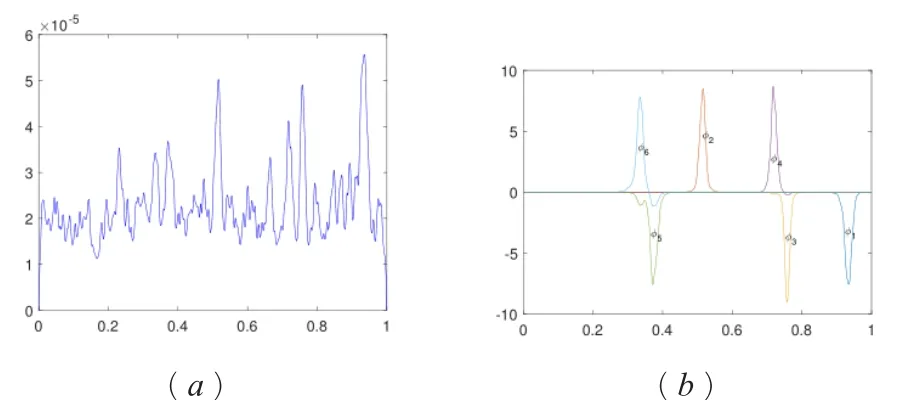
圖1 概貌函數（a）及前6個特征函數（b）

本節主要介紹特征值問題與源問題在一維與二維下的數值算例。所有數值實驗均使用C語言進行并行編程實現。數值結果中，一律以參數（P，M）分別表示分片常數隨機勢阱的隨機最大值與單個方向分片區域個數。所有未單獨標注的數值算例均經由N=10次分片多項式計算得到。

1．一維算例

一維算例均在工作站上完成，使用cpu核數為8。取（P，M）=（10e5，300）的分片勢阱V來模擬無序勢阱。

源問題的解（又稱概貌函數）和前6個特征函數的圖像如圖1所示。

從圖1中可以觀察到特征函數的高度局域化現象。疊加兩圖對比可以觀察到，每一個特征函數均對應局限于概貌函數的某一個波峰內。這兩種現象前者對應安德森局域化現象，后者對應概貌函數的控制理論。

對于（P，M）=（10e5，300）的一維特征值問題算例，采用基函數次數N=30的算例作為參考解，檢驗一維情況源問題對特征值的預測結果。

?

顯然，源問題預測特征解的理論的可靠性在一維情況下通過了檢驗，且數值結果與經驗性結論吻合。

2．二維算例

二維情況取參數（P，M）=（10e5，100）的算例來驗證概貌函數對特征的控制理論及預測理論。

圖2 概貌函數a及第一個特征函數（b）的等高圖

圖2展示了概貌函數與第1個特征函數的等高圖對比，我們發現特征函數的局域化區域可以被概貌函數預測。此外，結合參考特征值，可以得出概貌函數對特征函數的控制結論。

?

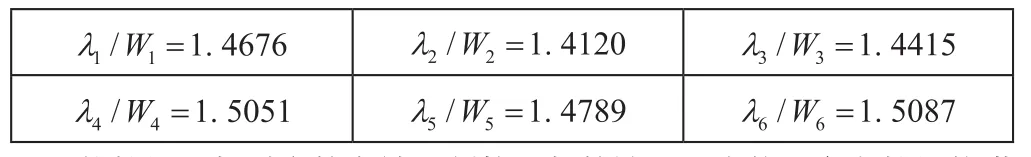
將特征函數對應的有效限制勢函數的波谷最小值與參考特征值進行對比，得到如上表所示的源問題對特征解的二維預測結果。

本文針對傳統有限元難以求解大規模勢阱問題及源問題的現狀，提出了譜元高效數值格式并設計了快速算法，完成了一維及二維情況下的大規模數值實驗，得到了更高精度的數值結果。本文提出的數值方法尚有進一步拓展的潛力，未來我們擬將該譜元方法應用于三維數值實驗，從而填補三維情況下的數值研究空白。