基于演化博弈的鐵路物流外包策略研究
楊文彬
(中鐵集裝箱運輸有限責任公司呼和浩特分公司,內蒙古 呼和浩特 010050)
1 引言
國務院在2014年印發的《物流業發展中長期規劃(2014-2020年)》中明確指出:將多式聯運工程列為十二大重點工程之首[1]。近年來受鐵路貨運改革和集裝箱運輸推廣的影響,多式聯運發展迎來了新的契機。各類扶持政策相繼出臺,高效、便捷的物流網絡和基礎設施基本建成,有效促進了多種運輸方式的順暢銜接。如何繼續提升物流體系綜合能力,加快多式聯運運輸效率,已成為影響多式聯運深入發展的關鍵因素。A Lozano、G Storchi(2001)提出時間算法,用以解決多式聯運中經營人對最優路徑的選擇問題[2]。Xiong,Wang(2010)設計的多任務多式聯運集成模型,有效地節約了運輸時間與成本[3]。F Russo,U Sansone(2014)通過對公鐵聯運碼頭周轉期的某些變量進行研究,解決了公鐵聯運的效率問題[4]。周建勤和米曉芳(2014)指出鐵路應專注于干線運輸,將兩端運輸委托給社會物流企業,構建以鐵路企業為核心的戰略物流聯盟[5]。孫雁勝和郝艷華(2014)探討了鐵路全程物流的兩端運輸,提出業務外包和構建汽運部的設想[6]。劉艦(2015)基于博弈的視角,提出了多式聯運過程中分運人的選擇機制[7]。崔德偉和彭永昌(2016)對物流業務外包、自營以及綜合三種模式進行了分析[8]。何明珂等(2016)根據物流系統接口理論構建數學模型,為多式聯運中各運輸方式間的銜接選擇提供參考[9]。朱漢民,姚華和劉斌(2018)從運作效率、技術效率、制度效率三方面入手,構建了集裝箱多式聯運效率評價指標體系[10]。當前國內外學者對多式聯運的研究主要集中于效用提升和模式選擇兩個方面,而對多式聯運企業間競合關系的分析相對欠缺。鑒于此,本文運用演化博弈理論,通過剖析多式聯運企業間競合關系,尋求影響聯運企業實現長期、穩定合作的關鍵因素并提出相關建議,以期為我國鐵路物流深入發展提供參考。
2 鐵路物流企業與外包車隊博弈關系分析
2.1 合作關系分析
(1)合作動因。一是具備優勢互補。鐵路運輸網絡遍及我國各大、中型城市,運量大、成本低、安全、環保等優勢彌補了汽運的不足;公路運輸則以其機動性好、靈活性強等優勢彌補當前鐵路兩端運輸的缺失。二是實現資源共享。鐵路物流企業可憑借外包車隊的設施、網點以及豐富的市場經驗有效組織兩端運輸;外包車隊則通過接受鐵路物流企業下達的訂單,獲取穩定貨源和物流收入。
(2)合作形式。目前我國鐵路物流企業與外包車隊主要采用契約式的合作形式,該種合作形式是雙方簽訂物流外包合同,并在后期執行過程中嚴格依照合同內容組織運輸。
2.2 不合作關系分析
(1)不合作的動因。一是拓展市場份額。近年來由于物流市場蓬勃發展,不少商家都看到其光明的前景,越來越多的企業進入市場參與競爭。想要在競爭激烈的物流市場中謀取進一步發展,拓展市場份額是必不可少的。二是獲取更多收益。收益不僅指企業所獲得的經濟指標,還包括企業名譽、技術水平、管理經驗等指標。當合作企業認為在合作情況下取得的收益會少于不合作情況下取得的收益,往往傾向于不合作。
(2)不合作的形式。不合作的形式有兩種:一是相互競爭,二是互不影響,獨立經營。其中競爭又分為惡性和良性競爭兩種形式。惡性競爭形式是價格戰,為戰勝對方,競爭企業間會不計后果的降低產品價格,直至把對手擠出市場。良性競爭形式是技術創新,通過研發全新的物流技術或設備提升競爭力,但此種競爭方式回報周期較長。
3 演化博弈模型構建
3.1 問題描述與模型假設
(1)假設鐵路物流企業在開展業務外包的過程中存在以下博弈主體:鐵路物流企業、外包車隊。其中,外包車隊負責組織兩端“門到站”和“站到門”的公路運輸,鐵路物流企業負責組織鐵路干線運輸并協調外包車隊的接取送達工作。
(2)假設:(a)有限理性。博弈各方都追求自身利益最大化,但由于自身因素的限制幾乎無法一次性選擇到最優策略。(b)存在演化博弈行為。在開展業務外包的過程中,博弈主體均存在演化博弈行為。
(3)博弈策略集合:在物流業務外包過程中,鐵路物流企業可選擇“合作”與“不合作”兩種策略;同樣,外包車隊選擇的策略也可能是“合作”、“不合作”。
(4)根據演化博弈問題描述,將有關參數做如下定義,見表1。

表1 變量及解釋
3.2 模型構建
依據問題描述與模型假設,建構鐵路物流企業與外包車隊收益矩陣,見表2。

表2 鐵路物流企業與外包車隊收益矩陣
鐵路物流企業選擇“合作”策略的期望收益為:

鐵路物流企業選擇“不合作”策略的期望收益為:
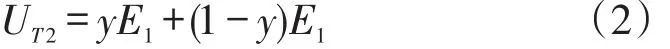
鐵路物流企業的平均期望收益為:
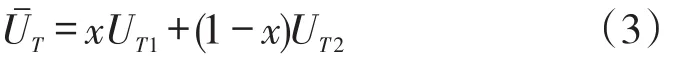
鐵路物流企業的復制動態方程為:

同理,外包車隊的復制動態方程為:

4 模型穩定性分析
根據上述內容,得到鐵路物流企業與外包車隊的雅可比矩陣:


根據定理可知,只有當所列均衡點行列式的值大于0,同時滿足它的跡小于0時,系統在該點處才能實現演化穩定的狀態。
(1) 當 αΔE<C1, (1-α)ΔE<C2時 ,故點G不在系統內,該系統中的均衡點分別為 A(0,0),B(0,1),C(1,0),D(1,1)。對上述四個均衡點做局部穩定性分析,見表3和圖1。

表3 局部穩定性分析

圖1 系統演化相位圖
在開展物流業務外包過程中,鐵路物流企業獲得的超額收益無法彌補其投入的成本,同時外包車隊獲得的超額收益也無法彌補其投入的成本。此種情況下,合作過程中雙方均未獲得收益。系統演化結果最終將趨于點A(0,0),即鐵路物流企業和外包車隊均會選擇不合作策略。
(2)當 αΔE>C1,(1-α)ΔE<C2時故點G不在系統內,該系統中的均衡點分別為 A(0,0),B(0,1),C(1,0),D(1,1)。對上述四個均衡點做局部穩定性分析,見表4和圖2。

表4 局部穩定性分析

圖2 系統演化相位圖
在開展物流業務外包過程中,鐵路物流企業獲得的超額收益大于其投入的成本,同時外包車隊獲得的超額收益無法彌補其投入的成本。此種情況下,雖然在合作過程中鐵路物流企業獲得了收益,但外包車隊卻未獲得收益,甚至可能出現虧損。系統演化結果最終將趨于點A(0,0),即鐵路物流企業和外包車隊均會選擇不合作策略。
(3)當 αΔE<C1(1-α)ΔE>C2時 ,故點G不在系統內,該系統中的均衡點分別為 A(0,0),B(0,1),C(1,0),D(1,1)。對上述四個均衡點做局部穩定性分析,見表5和圖3。

表5 局部穩定性分析
在開展物流業務外包過程中,鐵路物流企業獲得的超額收益無法彌補其投入的成本,同時外包車隊獲得的超額收益大于其投入的成本。此種情況下,雖然在合作過程中外包車隊獲得了收益,但鐵路物流企業卻未獲得收益,甚至可能出現虧損。系統演化結果最終將會趨于點A(0,0),即鐵路物流企業和外包車隊均會選擇不合作策略。

圖3 系統演化相位圖


表6 局部穩定性分析

圖4 系統演化相位圖
在開展物流業務外包過程中,鐵路物流企業獲得的超額收益大于其投入的成本,同時外包車隊獲得的超額收益也大于其投入的成本。此種情況下,鐵路物流企業和外包車隊會實現合作。但合作過程中G點位置改變,會影響雙方的合作結果。當G點位于折線BGC上方時,雙方最終會趨于合作;當G點位于折線BGC下方時,雙方最終會趨于不合作。
5 數值仿真驗證
借助MATLAB軟件運用數值仿真的方法,對上述推論作進一步研究。數值仿真圖中橫軸表示時間t,縱軸表示概率 p。
5.1 初始合作意愿
當ΔE=10,C1=3,C2=2,R=1,α=0.6,初始合作意愿分別為以下兩組值時,系統演化結果如圖5、圖6所示。
數值組1:x=0.73;y=0.82;
數值組2:x=0.41;y=0.53。

圖5 初始合作意愿數值組1仿真

圖6 初始合作意愿數值組2仿真
從圖5、圖6可以發現,當初始合作意愿變化時,雙方合作結果會發生改變。在上述條件下點G的坐標為(0.6,0.57)。當鐵路物流企業與外包車隊的初始合作意愿處于折線BGC的右上方時,雙方最終趨于合作;當鐵路物流企業與外包車隊的初始合作意愿處于折線BGC的左下方時,雙方最終趨于不合作。
5.2 超額收益
當 C1=3,C2=2,R=1,α=0.6,x=0.41,y=0.53,超額收益分別取以下兩組值時,系統演化結果如圖7、圖8所示。
數值1:ΔE=10;
數值2:ΔE=15。

圖7 超額收益數值1仿真

圖8 超額收益數值2仿真
從圖7、圖8可以發現,當超額收益變化時,雙方合作結果會發生改變。在其他條件不變的情況下,鐵路物流企業和外包車隊獲得的超額收益越高,雙方越趨于合作。
5.3 超額收益分配系數
當 ΔE=10,C1=3,C2=2,R=1,x=0.73,y=0.82,超額收益分配系數分別取以下兩組值,系統演化結果如圖9、圖10所示。
數值1:α=0.7;
數值2:α=0.6。
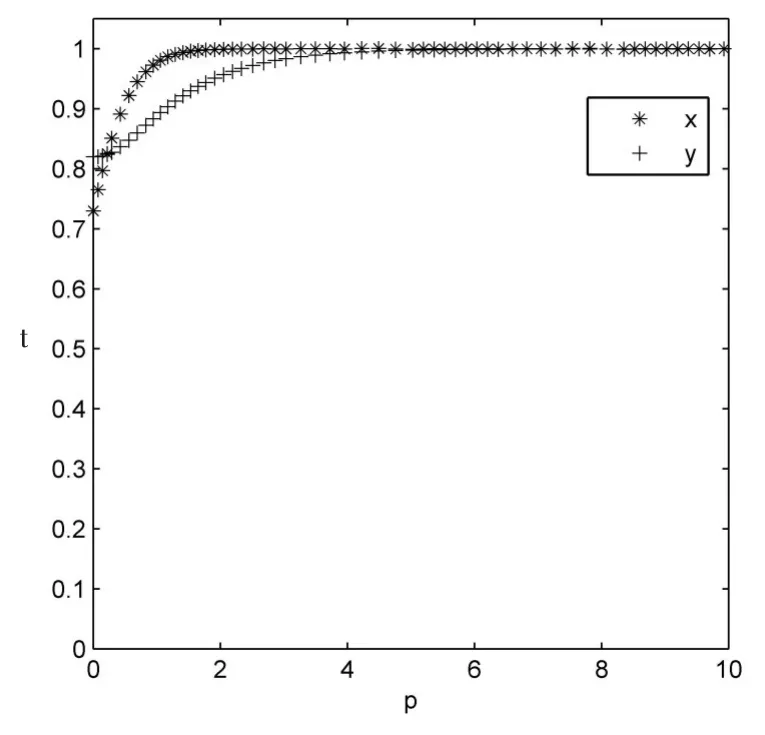
圖9 分配系數數值1仿真

圖10 分配系數數值2仿真
從圖9、圖10可以發現,當超額收益分配系數變化時,會加速雙方的合作結果。在其他條件不變的情況下,外包車隊超額收益分配系數越大,雙方實現合作的速度就越快。
5.4 企業投入成本
當ΔE=10,R=1,α=0.6,x=0.73,y=0.82,企業投入的成本分別取以下兩組值時,系統演化結果如圖11、圖12所示。
數值組1:C1=3,C2=2;
數值組2:C1=6,C2=4。
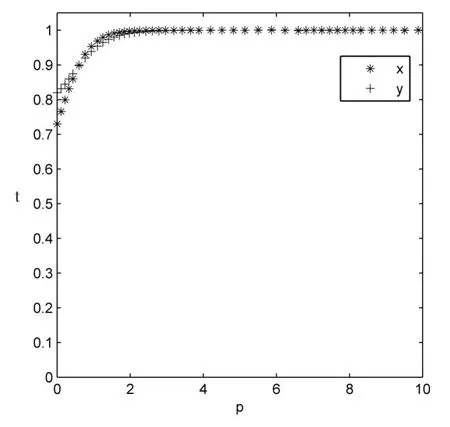
圖11 企業投入成本數值組1仿真
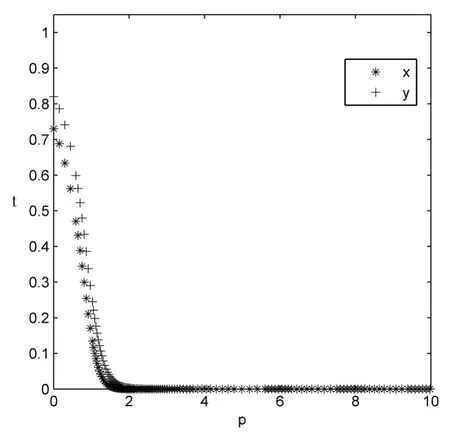
圖12 企業投入成本數值組2仿真
從圖11、圖12可以發現,當企業投入成本變化時,雙方合作結果會發生改變。在其他條件不變的情況下,鐵路物流企業和外包車隊投入的成本越低,雙方越趨于合作。
5.5 風險成本
當 ΔE=10,C1=3,C2=2,α=0.6,x=0.73,y=0.82,風險成本分別取以下兩組值時,系統演化結果如圖13、圖14所示。
數值1:R=1
數值2:R=8。

圖13 風險成本數值1仿真

圖14 風險成本數值2仿真
從圖13、圖14可以發現,當風險成本變化時,雙方合作結果會發生改變。在其他條件不變的情況下,鐵路物流企業和外包車隊認知到的風險成本越小,雙方越趨于合作。
6 結論
在對鐵路物流企業和外包車隊博弈關系分析的基礎上,從業務外包出發,運用演化博弈理論,構建了兩兩博弈的數學模型,指明了鐵路物流企業和外包車隊的策略選擇,主要結論如下:
(1)解決了鐵路物流企業與外包車隊合作共生發展沒有基于動態演化與有限理性視角考慮經濟收益與成本投入等影響的不足,指明了鐵路物流企業與外包車隊能夠協同發展的存在基礎。
(2)一方甚至雙方收益均受損時,鐵路物流企業與外包車隊出于自身利益考慮最終會趨于不合作;雙方超額收益均大于其投入成本時,鐵路物流企業與外包車隊最終是否趨于合作,受初始狀態和關鍵參數的影響。
(3)鐵路物流企業和外包車隊合作與否受初始合作意愿影響,會隨雙方超額收益和超額收益的分配系數增加而增大,隨雙方投入成本和風險成本的增加而減小。為了使鐵路物流企業和外包車隊能夠實現長期、穩定的合作,應該盡量創造超額收益并實現合理分配,合理安排運輸計劃降低投入成本,最大限度地減少風險成本的產生。

