高中數學解題敏捷性思維培養的幾點體會

浙江省諸暨市浬浦中學 蔡軍挺

筆者長期從事高中數學的教學實踐，就如何提高當前學生的數學解題能力，培養學生解題的靈活性、思維的敏捷性，談以下幾點體會：

一、仔細審題、推敲，培養學生解題的敏捷性

審題是整個解題思維過程的開端，它直接影響到整個解題過程的準確性和敏捷性。審題不嚴，百思不得其解；審題準確，解題時使人豁然開朗。

分析：這是一道典型的含參絕對值的函數問題，由于這類函數既帶有絕對值“攔路”，又含有參數“攪局”，因此許多學生感到茫然不知所措，一下子找不到問題的切入點。倘若我們能仔細審題、推敲，會發現對絕對值問題的突破是先去除絕對值，再利用函數的性質（單調性、奇偶性、最值等）并結合函數的圖像進行觀察分析，這是行之有效的途徑。

準確審題是培養學生解題能力的關鍵所在，那么怎樣才能準確審題呢？

1．認真閱讀試題，抓住問題的關鍵

在教學過程中，我們要求學生仔細閱讀題目，準確完整地理解題意。閱讀時應緊緊抓住試題中的關鍵詞句，反復推敲，如“任意的”“存在”“恒成立”等等，要防止粗枝大葉，一掠而過而誤解了題意。

2．尋找已知、未知，挖掘“隱含”條件

在審題時，要求學生分清“條件”和“結論”，特別是把那些“隱含”條件挖掘出來，使之充分“顯露”，正確了解題目涉及的概念和基本理論，理清它們之間的相互關系，從混亂中找到問題的突破口，尋找解決的途徑。

二、運用轉化思想，開啟數學解題的敏捷性

我們在教學過程中要引導學生利用已經積累的知識、經驗進行由表及里、由此及彼的遷移、轉化，使學生能在短暫的時間內迅速把需要的知識和經驗從知識結構體系中凸顯出來 ，使之在解答問題時有更多的機會獲得新靈感。

例2 （2016 年4 月浙江省學考17 題）已知平面向量滿足，其中為不共線的單位向量。若對符合上述條件的任意向量恒有，求夾角的最小值。

分析：本題體現了平面向量的轉化思想，利用向量模的運算轉化為向量運算。由恒成立，進而得到恒成立，得到恒成立，即得到恒成立，也就是恒成立，兩邊平方后得到恒成立，由于，本題進一步轉化為關于λ 的二次函數恒成立的問題，只要即可，從而解得最后轉化為余弦函數的問題來解決。本題通過知識點的不斷遷移，充分體現了轉化思想的魅力。

三、通過多種訓練，發展數學解題的敏捷性

數學教學中一題多解、一題多變、異題同解等練習，在訓練學生解題直觀性思維，培養學生敏捷性思維過程中是行之有效的。

例3 （2016 年諸暨市模考理7）已知△ABC 中，AC=2，AB=4,AC ⊥BC,點P 滿足最小值。

本題我們可以從多個不同的視角加以觀察、分析、思考，以達到發展學生解題敏捷性思維的目的。

解法1：直接利用平面向量的運算法則來解題。

解法2：從向量的坐標運算的角度來解決本題。

解法3：從考慮極化恒等式的角度來解決。

設M，N 分別為AB，AC 中點，

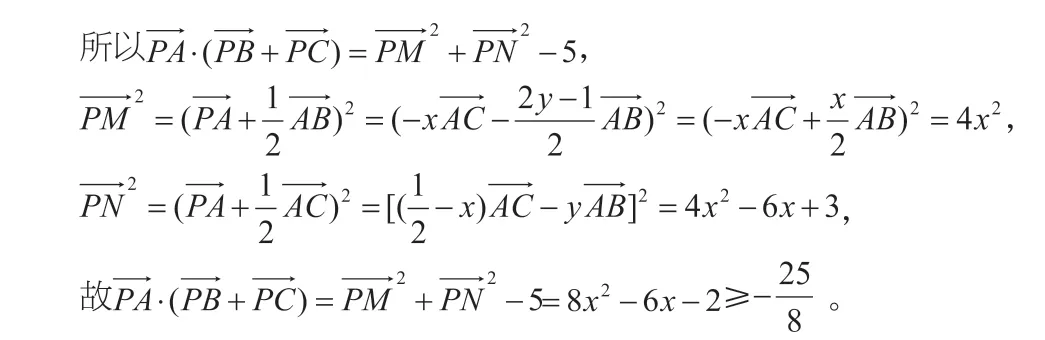
本題還有其他解法，還可以繼續挖掘，進一步拓展學生解題的視野。

這個條件，變式為：已知△ABC 中，AC=2，AB=4,AC ⊥BC,求的最小值，以達到一題多變的目的。

一題多變指在教學中要求學生不滿足表面現象，要抓住實質，揭示事物之間的內在聯系和變化規律，訓練解題思維的靈活性和敏捷性。

以上是筆者認為培養學生解題敏捷性思維能力的幾點體會，在教學過程中經常有目的、科學地對學生進行解題敏捷性思維能力的培養，對培養學生能力、提高教學效果等方面將取得事半功倍的效果。