算法思想在初中數學教學實踐中的研究

浙江省杭州市天杭實驗學校 季曉霖

在數學課程標準當中，已經明確指出對于算法多樣化的鼓勵和推崇，雖然目前初中數學教學中還并未對算法思想的運用進行明確規定，但其應用的有效性已經得到呈現。教育現代化視野下，教學領域面臨革新，迫切需要新的教學思想的融入和實踐，從而為初中數學教學的健康發展提供保障，這既是教育領域的發展要求，也是教育現代化視野下出現的新內容。將算法思想與初中數學教學全面融合，對促進初中數學教學實效以及學生的全面發展將產生積極影響。

一、算法思想概述

1．算法思想內涵

目前學術研究領域對于算法思想的界定并無統一標準，表述方面存在顯著差異，但從核心思想出發，其核心思想基本一致，即認為算法思想是一種解決問題的程序化、機械化的教學思想方法。

2．算法思想特征

算法思想本身具備以下幾個方面的特征：（1）有限性。算法思想的應用需要在一個限定步驟之內結束，即通過算法在短時間之內解決問題，突出算法的有效性。對于“有限性”的解讀，可以放在時間有限性和步驟有限性方面；（2）確定性。算法思想的應用，每一個計算步驟都需要確保準確性，避免發生歧義和模糊性因素。這一點與數學的核心思想保持較高的一致性，按照不同的步驟去執行和處理好各個步驟，最終輸出相應的結果；（3）可行性。算法思想的應用，每一個步驟都需要保證可行性，并且能夠得到被執行目標，在合理的范圍內去輸出結果；（4）有序性。算法思想在應用的過程中，需要按照嚴格步驟去具體執行，通過簡單而機械的方式來得到答案；（5）通用性。算法思想的應用不僅僅是解決一個單一的問題，而是能夠解決同類型的多個問題，具備通用性特點。總的來說，算法思想的基本特征賦予了算法思想獨特性和應用價值。

3．初中數學教學中運用算法思想的教學目標

將算法思想運用到初中數學教學中，需要有一個明確的教學目標提供支撐。為滿足數學教學的基本要求，確定教學目標如下：（1）能夠接觸自然的語言或者流程圖來解決方程、函數以及幾何知識點，并對于算法思想有一個最基本的了解，嘗試運用算法思想來解決部分問題；（2）對算法思想有一個初步的感知，能夠在獨立思考當中去培養發散思維，實現思維層面的創新；（3）運用多種方法去解決問題，將算法思想應用到初中數學教學具體實踐中，尋求解決方案的多樣性；（4）在不斷接觸和運用算法思想的過程中，對算法的程序化、機械化以及通用化的特征有所掌握，全面感受和體會算法思想的內在價值和精髓。

二、算法思想在初中數學教學實踐中的價值

1．培養初中生良好的思維習慣

從算法思想的內涵以及基本特征出發，將其應用到初中數學教學當中來，對于學生的思維習慣將產生重要影響。算法思想本身具備機械化和程序化的特色，對學生更好地掌握知識和技能具有積極作用，長期應用有助于學生自身形成條理化的思維模式。算法思想的應用，本身是由不同的結構組成，包括順序結構、條件結構以及循環結構。人在思考的過程中，當面臨復雜的問題和環境的過程中，需要從多角度著手，依據結構框架有一個清楚的認知，從而全面提高問題的解決效率。對于初中數學教學而言，算法思想的融入使得學生能夠掌握科學的問題解決方法，完成一系列同類問題的有效解決，從而鍛煉自己的思維習慣，對待問題本身有明確的條理性，逐步解決問題。

2．增強初中生數學思維能力

算法思想可以說是一種以解決實際問題為目的的高度概括的一個產物，算法本身就是一種邏輯順序和邏輯條理的微觀呈現，每一步處理程序、每一個過程都有明確的邏輯依據。將算法思想融入初中數學教學中，使得學生對于算法思想有一個基本的了解和認知，從而在數學思維能力的培養方面展現出算法思想的應用有效性。相比于固化的教學思想，算法思想的應用能夠提高學生思維的靈敏度，探究一種全新的數學思維框架，對學生數學思維能力的培養將產生積極作用。總的來說，算法思想融入初中數學課堂當中來，對初中生的數學思維能力將產生積極影響，效用顯著。

3．更深層次地接觸和學習算法知識

初中階段的算法思想，學生初步了解和感知即可。初中階段的算法思想主要是增強學生的感知，去學習和接觸更多的算法知識，從而為后續更好地應用算法思想奠定基礎。雖然算法思想在初中階段的應用是基礎階段，但也需要注意整個過程中學生對于算法思想的理解程度。在初中課堂當中，算法思想可以被融入各類型的課程教學中，為后續的學習奠定堅實基礎。當然，算法思想想要在初中數學教學中發揮出應有的作用，并非一蹴而就，而是一個循序漸進的過程。初中階段學生對于算法思想的理解和掌握程度，將對后續的學習產生深遠影響。

三、算法思想在初中數學教學中的具體實踐

1．算法思想在方程教學中的實踐

在算法思想中，化歸思想是其中的重要思想內容之一。化歸思想在初中數學方程教學中經常被應用。例如在求解一元一次方程的過程中，具體過程涵蓋了去分母、去括號、移項、合并同類項、系數化為1 的整個步驟；二元一次方程組求解，通常采取消元法和代入消元法；求解分式方程，多是要將其化為整式方程，然后求解、驗根，得到方程的解。不同方程的求解過程，都體現了算法思想當中的化歸思想。基于此，以分式方程為例，將算法思想應用到分式方程的求解當中，教學過程如下：

師：同學們應該都知道在一元一次方程的求解過程中，第一步是什么？

生：去分母。

師：解分式方程的第一步和一元一次方程相同，也是去分母。如分式方程，在求解過程中，則要聯想一元一次方程的去分母過程，同學們還知道一元一次方程如何去分母嗎？

生：方程兩邊同時乘以分母的最小公倍數。

師：如果分母中含有字母呢？

生：方程兩邊同時乘以最簡公分母。

師：那這個分式方程的最簡公分母是什么？

生：（x-5）（x+5）。

師：非常好，那么分式方程去分母之后，化為整式方程，現在得出的方程是什么形式？

生：x+5=10。

師：現在這個分式方程已經成為我們傳統的一元一次方程，第二步則是求解方程，這個方程的解是多少？

生：5。

師：分式方程的分母不能為0，最后步驟則需要驗根，將5 代入分式方程當中，看最簡公分母是否為0？

生：為0。

師：這就說明這個方程無解。現在大家總結一下分式方程的求解步驟。

生：第一步，去分母，化為整式方程；第二步，解整式方程；第三步，驗根。

在分式方程中將算法思想充分應用，能夠讓學生明白驗根的重要性和為什么需要驗根。相比于傳統的教學模式，這種教學所展現出的效果更好，能夠讓學生初步感知算法思想，并運用算法思想來解決分式方程的相關問題。

2．算法思想在函數教學中的實踐

函數內容是初中數學教學中的重要組成部分，算法思想在函數教學當中的應用實踐，所展現出來的效果良好。為展現算法思想的應用價值，將其應用到一次函數教學當中來，設計教學方法如下：

師：當前，已知一次函數圖像過點（3，5）與（-4，-9），求這個函數的解析式。

師：求一次函數y=kx+b 的解析式，關鍵在于求出k，b 的值，從已知條件當中可以列出有關于k，b 的二元一次方程組，并求出k，b，所以在這里我們首先需要做什么？

生：設函數解析式為y=kx+b（k ≠0）。

師：非常好，因為直線y=kx+b 過點（3，5）與（-4，-9），所以下一步要怎么做？

師：同學們回憶一下之前解方程組的步驟，下一步需要做什么？

師：最后我們根據這個結果，得出這個方程的解析式為y=2x-1。這種求函數解析式的方法被稱之為待定系數法。對整個步驟進行總結，具體分為4 步：（1）設函數解析式；（2）列方程組；（3）解方程；（4）代入函數解析式。下面大家運用待定系數法去解決書中的課后練習題。

該教學案例則是將算法思想充分融入一次函數的教學當中，通過教師的有效引導，學生能夠通過自身所儲備的知識去解決問題，掌握使用待定系數法來求解函數解析式的算法思想。算法思想與實際問題的有效融合，對學生更深刻地理解算法思想具有積極意義。

3．算法思想在幾何教學中的實踐

算法思想在幾何教學中的應用實踐，以勾股定理的教學為例，其作為幾何知識點當中的關鍵內容，勾股定理主要是表現三角形三邊之間的數量關系，雖然內容看似較為簡單，但該內容通常具有廣闊的應用空間，在各個綜合性的知識點當中均有所應用。將算法思想應用其中，如：已知△ABC 的三邊長為a，b，c（a ＜c，b ＜c），判斷該三角形是否為直角三角形，算法設計如下圖所示：

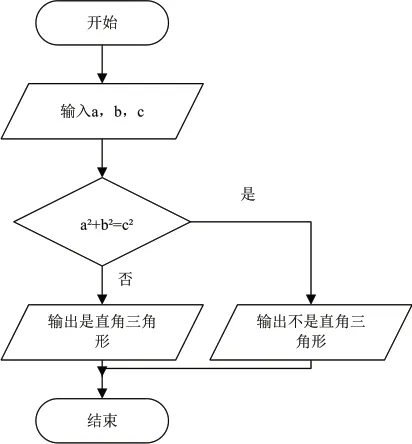
勾股定理的算法設計圖

勾股定理的算法設計，結合教師的講解，使得學生對于算法思想的認知度全面提升，通過該算法，用勾股定理判斷直角三角形的過程更直觀，學生對于算法知識的了解也更全面，所展現出來的效果更好。

四、算法思想在初中數學教學中的實踐策略

算法思想在初中數學教學中的具體實踐，將其分別應用到方程、函數以及幾何知識點教學當中，所展現出來的應用效果顯著，為教學實效性的提升以及學生更好地了解算法思想奠定了基礎。但需要注意的問題是，想要算法思想發揮出更高的有效性，還需要制定實踐策略，具體從以下幾個方面著手：

1．滲透式教學

算法思想有效融入初中數學教學實踐當中是一個相對漫長的過程，需要教師在開展教學實踐的過程中，將這種思想滲透到教學實踐中來，與數學教學內容充分融合。這樣，學生在參與到數學課堂學習中時，則能夠潛移默化地提升自己對于算法思想的認知度，從而在升入高中之后適應性得以全面提升。

2．算法化教學

相比于滲透式教學模式，算法化教學效果更直接。但還是需要借助滲透式教學模式，使得學生初步了解和掌握算法思想的內容。算法化教學則是對算法化的構造進行設計。在數學教學內容的選擇方面，要做好篩選，選擇具有典型代表性的教學內容，凸顯出算法思想的機械化和程序化的特征，以算法構造為核心，在數學教學內容中充分展現算法的本質。

3．鼓勵算法教學多樣化

算法思想融入數學教學當中來，帶來了數學教學發展新空間，使得數學教學別具魅力。算法教學的多樣化使得教學內容更明確，對解決不同類型的數學問題具有積極作用。一方面，學生能夠在算法教學多樣化當中去提高解題效率和鍛煉解題能力，另一方面，教師也能夠在算法多樣化當中提高自己的綜合能力，走向專業化方向。可以說，算法教學的多樣化，能夠使得算法思想更好地融入數學教學實踐當中。

4．強化算法教學與信息技術之間的關聯

算法思想本身屬于一種數學思想方法，與計算機科學之間保持著緊密的聯系，算法思想與信息技術的完美融合，使得傳統數學知識的解決方法更直觀，效果更好。當然，將其應用到初中數學教學實踐中，對學生學習興趣的提升作用顯著。

綜上所述，初中數學教學對于學生的全面、綜合發展具有積極意義。算法思想的融入，賦予了傳統教學新的發展空間。借助算法思想，對于學生的綜合發展將產生積極影響。同時，算法思想的融入，為學生后續的數學學習提供了諸多便捷性，值得全面推廣應用。