例析高一數學三角形中的中線問題
江蘇省南京市棲霞中學 張鴻博
向量是高中數學的重要內容,在教學中占據重要地位。具體來說,向量既有代數運算,可以進行相加、相減、數乘和數量積運算,又有幾何特征,可以用它來證明直線平行、垂直,同時它又有豐富的物理背景,可以類比物理中的速度、加速度、位移等。學好向量對于我們以后的學習很有幫助,這就要求學生形成一個正確的向量概念,深刻理解其內涵。
在高一數學中,有一類三角形的問題學生屢做屢錯,例如:
在△ABC 中,AD 是BC 邊 上 的 中 線, 已 知∠A=120 °,AB=4,AC=6,求AD 的長。
【分析】此題明顯是以三角形為背景的題目,學生看到題目的第一反應是運用解三角形的相關知識:
【錯解】在△ABC 中,

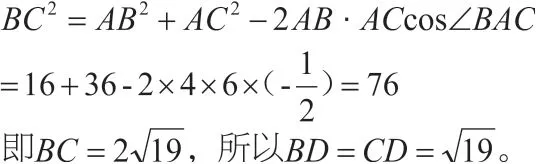
到此為止,準備工作已經完成,接下來要求AD 的長,而在△ABD 中,我們只有AB=4,,兩個條件解三角形是不夠的,同理,在△ACD 中,解三角形的條件也不足,所以學生到這里就做不下去了。
我們來反思一下,為什么上述方法不成功呢?直接原因當然是條件不夠,那根本原因是什么?是中線AD 把∠A=120°分成了兩個角,而這兩個角我們都不知道,所以我們才會缺少條件。
于是,這道題的問題就變成了如何在只知道大三角形中的兩邊及一夾角的情況下,求出大三角形內部的一根中線的問題,那我們該如何解決這個問題呢?
兩邊及一夾角,除了和余弦定理有關,還和向量的數量積有關!
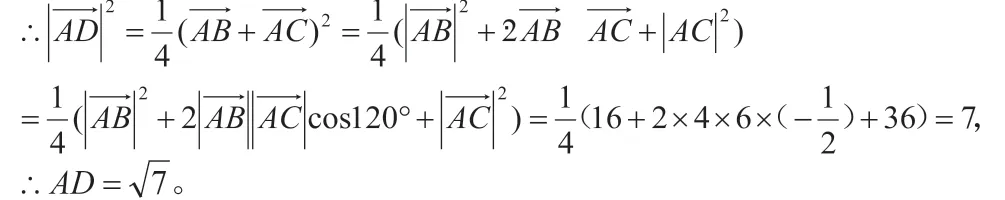
此題除了上述解法外,還有其他方法。上題的難點在于中線AD把∠A=120°分成了兩個角,而這兩個角我們都不知道。雖然兩個角都不知道,但是我們知道這兩個角的和,所以我們可以把這兩個角“打包”,讓它們同時出現,于是我們想到了這樣的方法:
【解法二】如右圖所示,把△ABD 繞D點旋轉80°,不難證明△ABD ≌△A′CD,

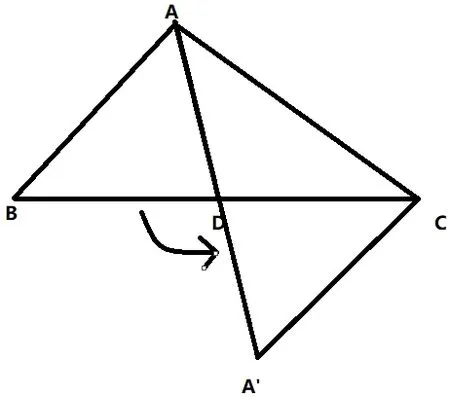
在△ACA′中,即AC=6,A′C=4,
由余弦定理得:AA′2=AC2+A′C2-2AC·A′C·cos∠ACA′=16+36-


