立體幾何中的動態題

王蘇文

(浙江省諸暨市浬浦中學 311824)

動態題是立體幾何中的常見題型，但此類問題對部分學生而言有一定的難度，有時往往望而卻步，筆者通過幾例動態題分享處理此類問題的常見策略.

一、由動變定

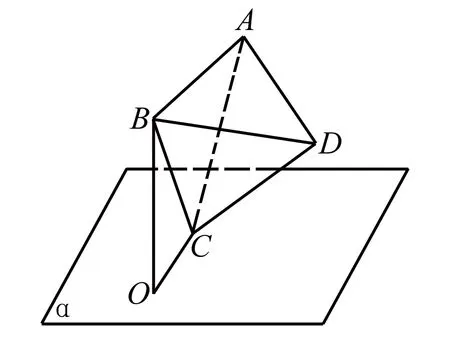
圖1

動態題最大的難點是不斷變化，假如能抓住這個變化問題的規律，找到所求問題的關鍵位置，那么問題就可迎刃而解了.

例1 如圖1，正四面體ABCD的頂點C在平面α內，且直線BC與平面α所成的角為45°，頂點B在平面α內的射影為點O.當頂點A與點O的距離最大時，直線CD與平面α所成角的正弦值等于( ).

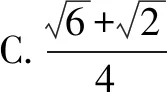
從題中可看出，實際為△ABC繞邊BC旋轉，要想O、A兩點距離為最大，只需面BOC與面ABC共面即可.

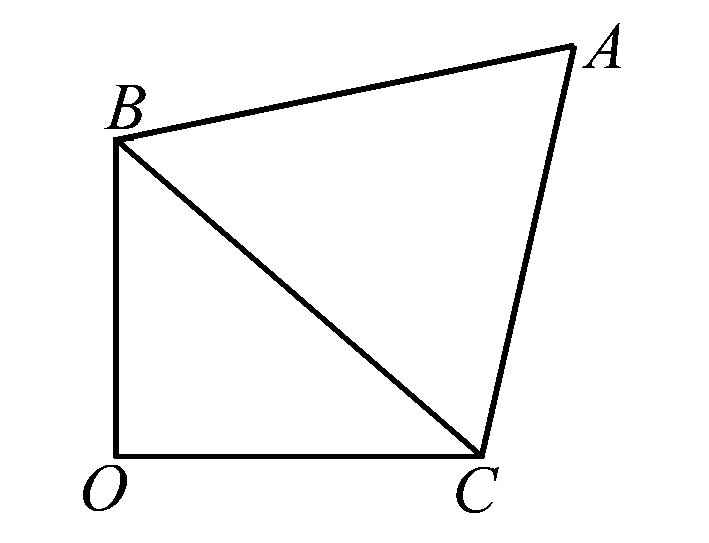
圖2

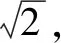
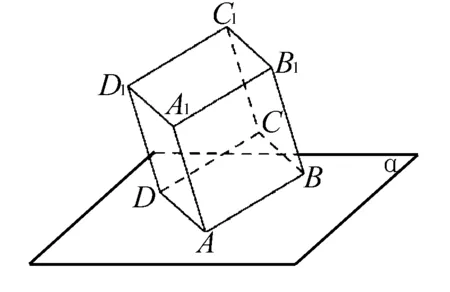
圖3

本題運用傳統法或空間直角坐標系來求解有所困難，而空間基底向量也是解決這個問題的又一亮點.

例2 如圖3，棱長為4的正方體ABCD-A1B1C1D1，點A在平面α內，平面ABCD與平面α所成的二面角為30°，則頂點C1到平面α的距離的最大值是( ).

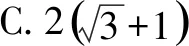
本題的運動變化是面ACC1A1中的線AC繞點A在面ABCD內運動，要想使點C1到平面α的距離最大，實際只需點C到面α的距離最大即可.原題變為：在面ABCD內點C到面α距離最大.

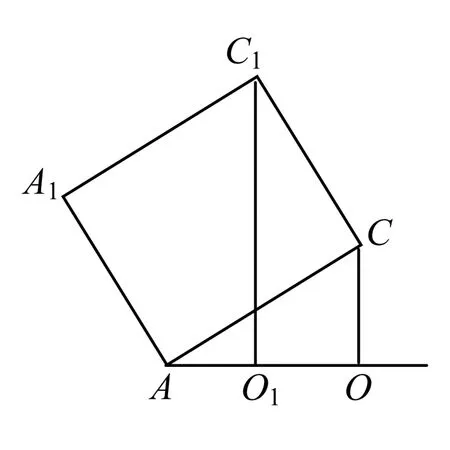
圖4

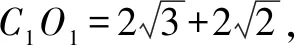
上述兩題充分利用旋轉規律找到最佳位置，即動態題轉化為固定位置題，從而實現由動變定的轉化.

二、由幾何變代數

立體幾何動態題的最大障礙是變化不定，假如能將幾何問題轉化為代數問題，何嘗不是一種好的策略.

例3 在長方體ABCD-A1B1C1D1中，AB=BC=2，AA1=1，若E，F為BD1的兩個三等分點，G為長方體ABCD-A1B1C1D1表面上的動點，則∠EGF的最大值為( ).

A．30° B．45° C．60° D．90°

作為常見幾何圖形長方體，建……