基于貝葉斯網絡的聯網環境中跟車工況下的前車運動狀態預測?

張金輝，李克強，羅禹貢，張書瑋，李 紅

(清華大學，汽車安全與節能國家重點實驗室，北京 100084)

前言

近年來，以雷達和計算機視覺為代表的先進環境感知技術迅速發展，推動了汽車智能駕駛系統的產生，大大提高了車輛性能。如車道偏離預警、前方防碰撞預警系統和緊急制動系統等，提高了車輛行駛安全性，自適應巡航控制系統、自動泊車系統等降低了車輛駕駛負擔。

傳感器的產生提高了車輛對自身和外界環境的感知能力[1]，并通過分析獲取的感知信息，判斷自身及周圍物體的運動狀態信息，作出決策并執行。科學理論的不斷完善迅速地提升著智能系統的預測能力，即基于已有感知信息對自身或周圍環境未來狀態的感知能力，如：文獻[2]中基于駕駛操作特征和隱馬爾可夫模型對駕駛員跑偏駕駛、一般轉向和緊急轉向等的駕駛行為進行預測，有助于及時糾正或干預駕駛員正在或即將發生的危險操作；文獻[3]中基于卡爾曼濾波的預測自車未來時刻可能的行駛運行狀態，可降低車輛碰撞風險，提高車輛的主動安全性。

跟車工況下的車輛特性又稱為跟馳特性，指動態跟車工況中，駕駛員采用的加速度與車間狀態和車輛狀態的關系，反映了駕駛員調整自車運動軌跡的操作習慣，且在城市交通流中，動態工況占跟車工況的大部分。現有跟車工況下車輛特性研究如下所示：文獻[4]中對影響跟車行為的人為因素和環境因素進行分析；文獻[5]中針對低速交通條件下的車輛跟馳問題，使用儀器測量收集的奧斯陸、巴黎和南安普敦3個歐洲城市的涵蓋城市高速公路、城市主干道和城市街道的各種交通狀況數據，對駕駛員行為進行分析，研究了低速交通條件下的時間間隔和距離間隔，并與高速交通條件下的時間間隔和距離間隔進行了比較，旨在評估先進的駕駛員輔助系統和自動車輛導航系統對可持續城市發展的貢獻程度；文獻[6]中提出一種假設跟馳模型，認為駕駛員通過加速或減速操作與周圍交通環境交互，并認為車輛加速度/減速度與期望速度與實際速度差、期望車間距離與實際車間距離差成比例關系；文獻[7]中基于常用的駕跟車模型Gipps模型和IDM模型，將駕駛任務難度度量為駕駛任務需求與駕駛能力之間的動態交互，提出TDGipps模型和TDIDM模型，通過車輛軌跡數據對提出的模型進行參數標定，并驗證了模型的有效性，以解釋影響跟車行為的規則因素和人為因素；文獻[8]中提出一種包括經典的刺激-反應框架、廣泛的五層結構和感知-預期-推理-策略-行動的模型以及基于模糊邏輯的推理機制，預測駕駛員與前方車輛相互作用時的駕駛行為和心理過程，并通過實驗證明了模型的穩定性；文獻[9]中對濟南市某信號交叉口的現場跟車數據進行了數據挖掘，指出前車速度的變化對后方車輛運動有顯著影響，并提出了一種考慮單行道上緊鄰前方車輛速度差的改進跟馳模型。

隨著信息技術、計算機技術、網絡技術和通信技術的不斷發展，以及人們對高品質生活的追求，車聯網概念被提出，目的是為提高人們出行交通安全性、舒適性和便捷性等。車聯網是以車內網、車際網和車載移動互聯網為基礎的由車輛位置、速度和路線等信息構成的大型信息交互網絡。車聯網環境中的車輛通過GPS、傳感器和攝像器等設備獲取自身和周圍環境信息，并通過互聯網技術完成自身信息與周圍車輛和交通設施信息的交互。

處于車聯網的車輛可以實時通過網絡獲取周圍車輛運動狀態信息，并通過一定分析方法對車輛未來時刻的運動行為或狀態進行預測。城市交通環境中，車流密度較大，跟隨前車行駛工況時常發生。文獻[10]中通過構建無線傳感網絡移動節點的運動模型，提出一種基于運動預測蒙特卡洛定位算法，進行節點位置預測。由于跟車工況中，車輛運動狀態受駕駛員駕駛風格和前方車輛運動狀態等多種因素影響，現有運動狀態預測方法無法直接應用于跟車工況的前車運動狀態預測，因此本文中對聯網環境中跟車工況下的前車運動狀態預測進行研究。

1 跟車工況下的前車運動狀態預測

1.1 車聯網環境中跟車工況下的前車運動狀態預測問題描述

隨著車輛數量的逐年增加，城市交通環境中，車流密度較大，跟隨前車行駛工況時常發生。若能通過車聯網信息獲取前方車輛運動狀態信息，后方車輛可根據獲取的信息對前方車輛運動狀態進行預測，可以為車輛智能系統提供控制依據，以提高車輛行駛性能，如降低能耗的節能控制、提高駕駛安全性的碰撞預警控制和提高舒適性的自適應巡航控制等。車聯網環境中的跟車工況及跟車工況下的前車運動狀態預測如圖1所示。

圖1中車輛A為自車，車輛B為前車，車輛C為前前車。設當前時刻為第i時刻，定義：vpp(i)為第i時刻前前車的速度；app(i)為第i時刻前前車的加速度；vp(i)為前車B第i時刻的速度；ap(i)為前車第i時刻的加速度；d(i)為第i時刻前車與前前車的相對距離；Δv(i)為第i時刻前車與前前車的相對速度；vpp(i＋j｜i)為第 i時刻預測的第 i＋j前時刻前前車的速度；app(i＋j)為第i時刻預測的第 i＋j時刻前前車的加速度；vp(i＋j)為第i時刻預測的前車第i＋j時刻的速度；ap(i＋j)為第i時刻預測的第i＋j時刻前車的加速度；d(i＋j)為第 i時刻預測的第 i＋j時刻前車與前前車的相對距離；Δv(i＋j)為第i時刻預測的第 i＋j時刻前車與前前車的相對速度；j＝1，2，…，n。

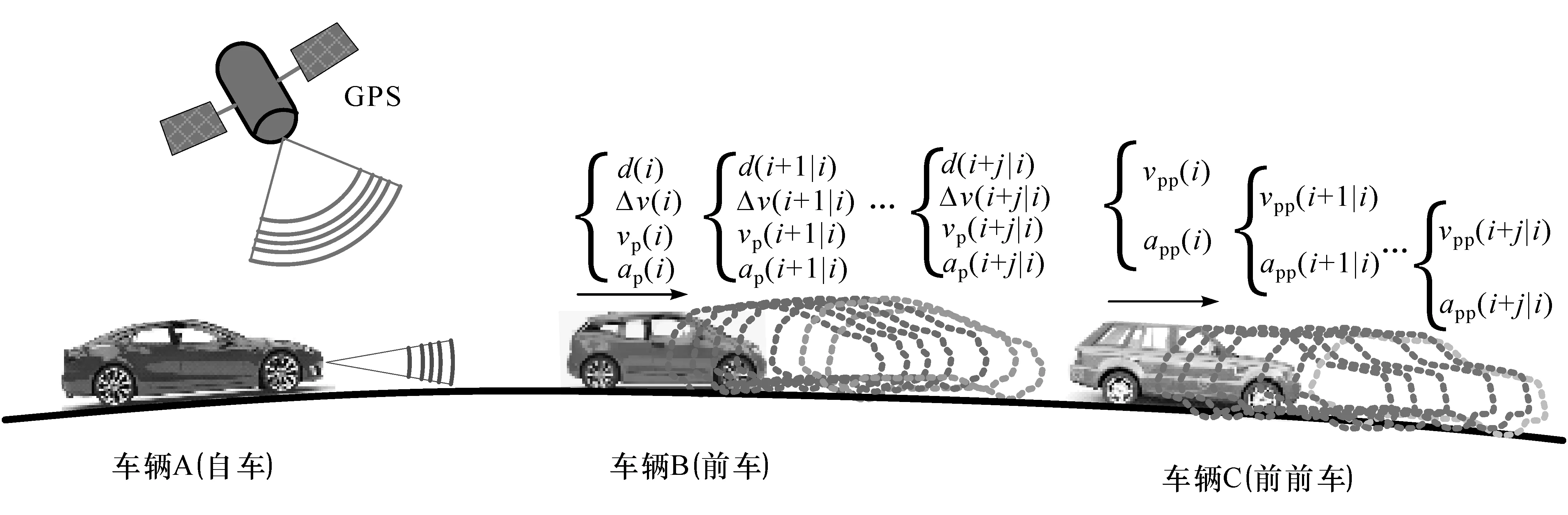
圖1 聯網環境中跟車工況下的前車狀態預測示意圖

1.2 跟車工況下的前車運動狀態分析

現有的駕駛員跟車模型多用于微觀交通流等領域，具有結構復雜、參數多、包含強非線性環節等缺點，因此本文中采用道路實驗方法獲取跟車工況下的車輛運動信息。在實驗過程中，以自車運動狀態代表圖1中的前車，即車輛B；以前方第一個車輛代表圖1中前前車，即車輛C；得到包括時間、前前車速度、前前車加速度、前車與前前車相對距離、相對速度、前車速度和前車加速度等跟車工況下車輛行駛數據信息。

本文中實驗車輛為戴姆勒S級350-L，在實驗車上裝載用于收集行駛數據的Velodyne HDL-64E S2型三維激光雷達，自身運動狀態信息從CAN總線獲取，采集頻率為10 Hz。測試路線有荷清路、知春路、海淀區校園南路、海淀區薊門里北路、海淀區北三環中路和海淀區北二環中路等城市道路，總距離為17.8 km。男性駕駛員37人，女性駕駛員13人，共50名。實驗時間為每人1天，共50天。在駕駛數據采集過程中，駕駛員不受外界行為指導，根據實時交通工況自然駕駛。

在道路實驗過程中，受駕駛隨機性、道路結構和交通狀況等因素影響，車輛行駛工況比較復雜，實驗結果含有非跟車工況數據，本文中參照文獻[11]建立符合我國交通流特征的跟車工況判斷準則，篩選出如下跟車工況行駛數據。

(1)為排除自由駕駛工況，要求前車前方存在有效車輛，車間距離滿足

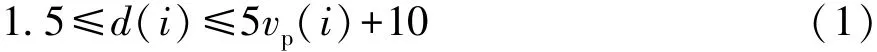
(2)為排除前車切入切出工況，相鄰采樣時刻的車距滿足

(3)為排除緊急制動工況，相對車速滿足

(4)連續跟車過程中，前車加速度80%以上的數據點滿足

(5)連續跟車過程中，前車加速度滿足

(6)連續跟車時間大于10s，且無停車、起步過程。

將獲取的跟車工況下的車輛行駛狀態數據分成兩部分：一部分用于訓練前車運動狀態預測模型，另一部分用于驗證前車運動狀態預測模型。

根據上述準則選取跟車工況數據集，在跟車數據的基礎上采用統計方法分析跟車工況車輛運動特性，如圖2～圖7所示。

圖2 跟車工況下前車速度概率分布

由圖2～圖7可知，跟車工況下前前車的速度及加速度、前車的速度及加速度和前車與前前車的相對距離及相對速度近似高斯分布。因此，本文中聯合高斯分布和貝葉斯網絡進行前車狀態預測研究。

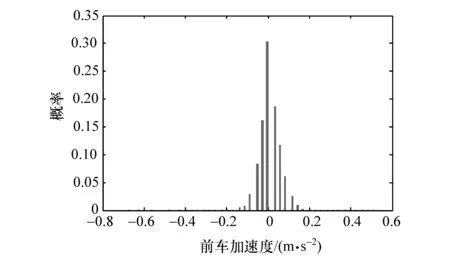
圖3 跟車工況下前車加速度概率分布

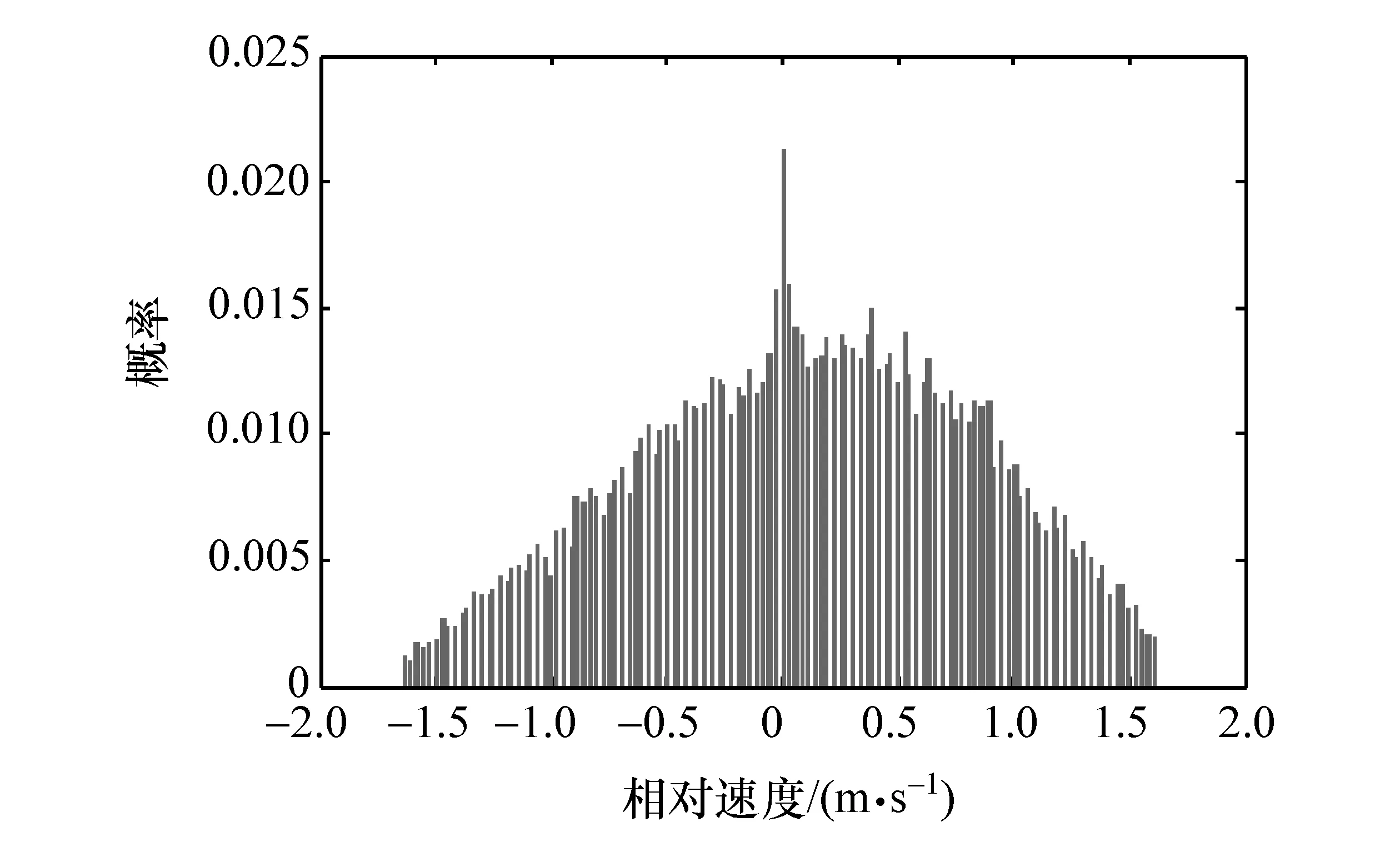
圖7 跟車工況下前車與前前車的相對速度概率分布

2 基于貝葉斯網絡的前車狀態預測

2.1 貝葉斯網絡簡述

貝葉斯網絡是一種概率網絡，它是基于概率推理的圖形化網絡，是Pearl于1988年為解決不定性和不完整性問題而提出的。一個貝葉斯網絡是一個有向無環圖(directed acyclic graph，DAG)，由代表變量節點及連接這些節點有向邊構成。節點代表隨機變量，節點間的有向邊代表了節點間的互相關系(由父節點指向其子節點)，用條件概率進行表達關系強度，沒有父節點的用先驗概率進行信息表達。節點變量可以是任何問題的抽象，適用于表達和分析不確定性和概率性的事件，應用于有條件地依賴多種控制因素的決策，可以從不完全、不精確或不確定的知識或信息中做出推理，在多個領域中獲得廣泛應用。

貝葉斯網絡特點如下：

(1)貝葉斯網絡本身是一種不定性因果關聯模型，貼切地蘊含了網絡節點變量之間的因果關系及條件相關關系；

(2)貝葉斯網絡通過條件概率表達各個信息要素之間的相關關系，能在有限的、不完整的和不確定的信息條件下進行學習和推理，因而具有強大的不確定性問題處理能力；

(3)貝葉斯網絡各種信息納入網絡結構中，按節點的方式統一進行處理，能有效地按信息的相關關系進行融合。

因此本文中根據已知的跟車工況中車輛的運動狀態，基于貝葉斯網絡，對車輛未來時刻的跟車運動狀態進行預測。

2.2 車輛狀態預測貝葉斯網絡結構設計

根據先驗知識與圖2～圖7所示實驗數據特性，分析各變量相互關系，設計i時刻各狀態依賴關系，如圖8所示，各狀態變量概率分布如式(6)所示。

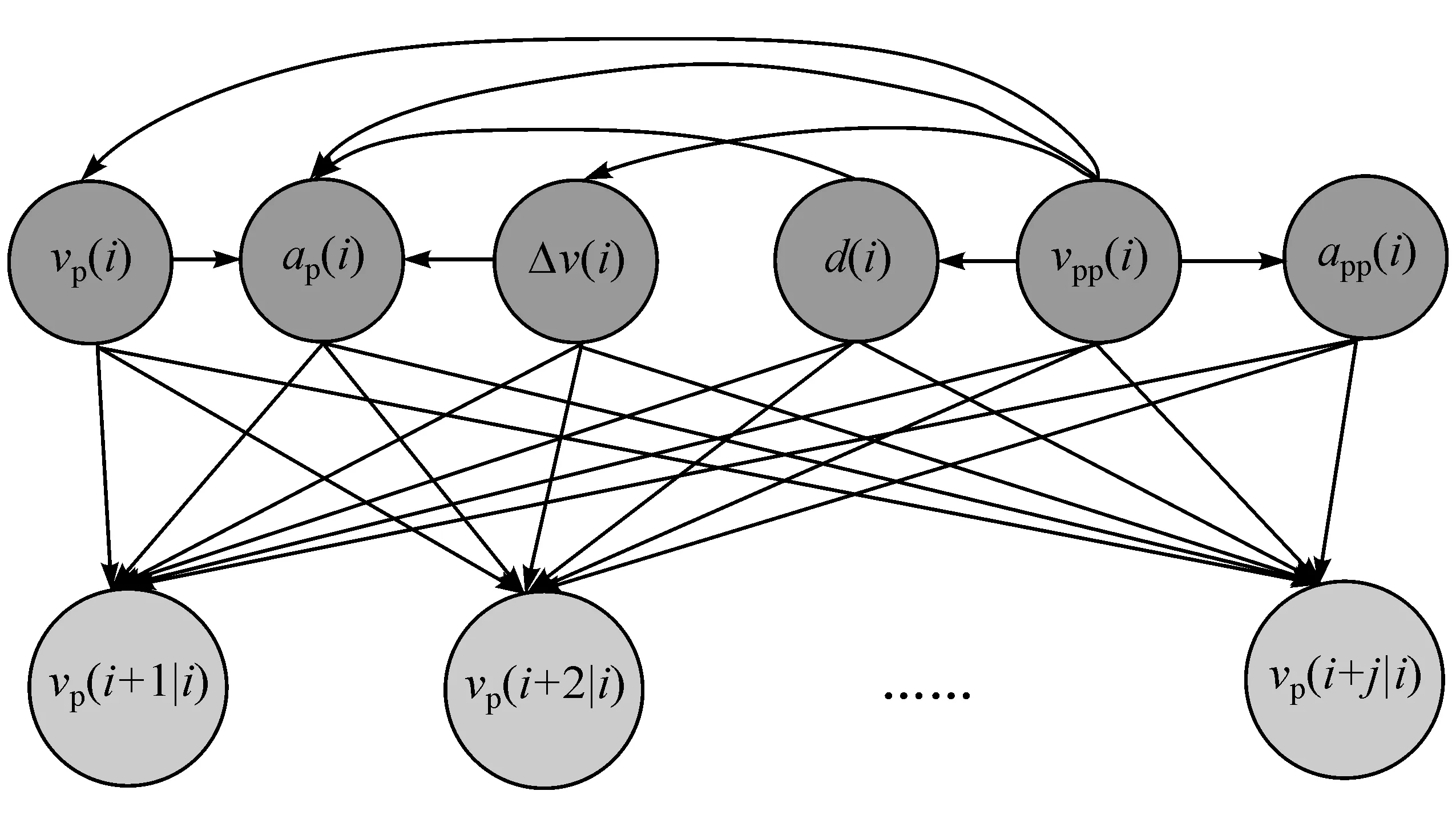
圖8 基于i時刻狀態預測i＋j時刻前車車速的貝葉斯網絡

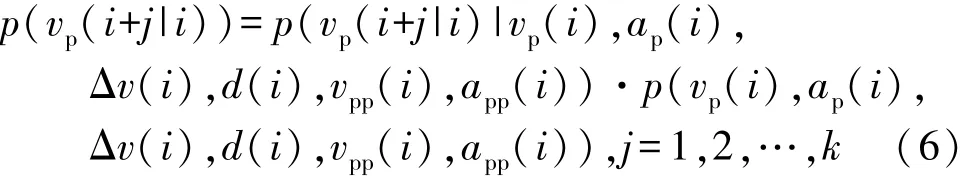
設 vpp(i)獨立分布，app(i)，vp(i)，Δv(i)，d(i)分別依賴vpp(i)獨立分布，ap(i)依賴 vpp(i)，app(i)，vp(i)，Δv(i)和 d(i)分布。 式(6)中：

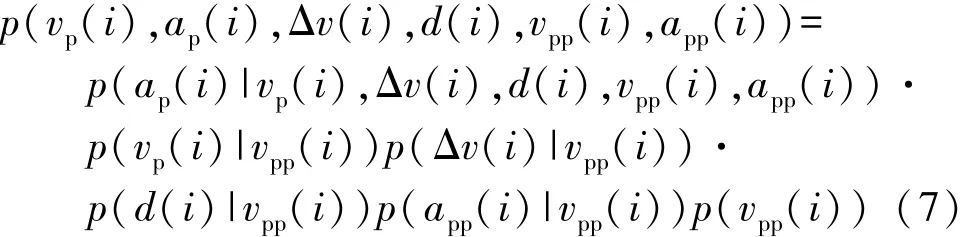
設i時刻狀態變量vpp(i)的概率分布為

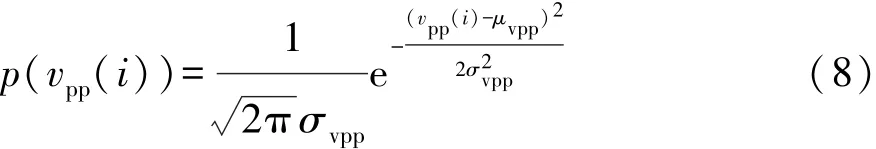
式中μvpp和σvpp分別為i時刻狀態變量vpp(i)的期望和標準差。

設i時刻狀態變量app(i)，vp(i)，d(i)和Δv(i)的條件概率分布為

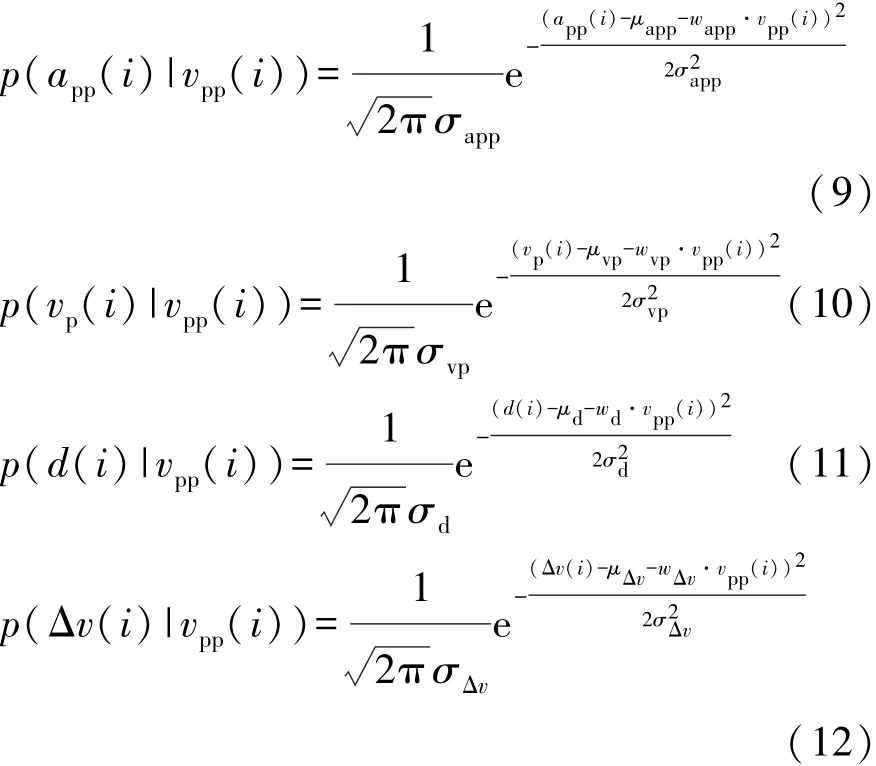
式(9) ～ 式(12)中：μapp，μvp，μd和 μΔv分別為 app，vp(i)，d(i)和 Δv(i)的期望的常量；wap1，wap2，wap3和wap4分別為 vp(i)，Δv(i)，d(i)和 vpp(i)的權值系數；σapp，σvp，σd和 σΔv分別為app，vp(i)，d(i)和Δv(i)的標準差。

式中 wap1，wap2，wap3和 wap4分別為 vp(i)，Δv(i)，d(i)和vpp(i)的權值系數。設i時刻狀態變量ap(i)的條件概率分布為

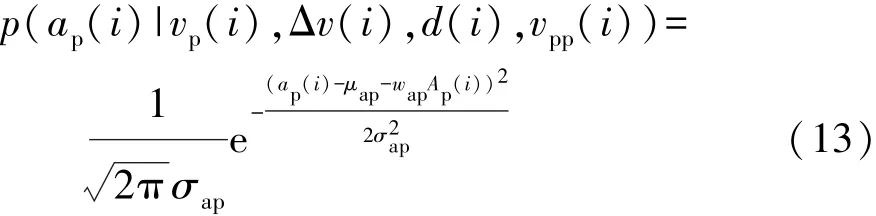
式中 wj，1， wj，2， wj，3， wj，4， wj，5和 wj，6分 別 為 vp(i)，ap(i)，Δv(i)，d(i)，vpp(i)和 app(i)的權重。 i＋j時刻狀態的條件概率分布函數為

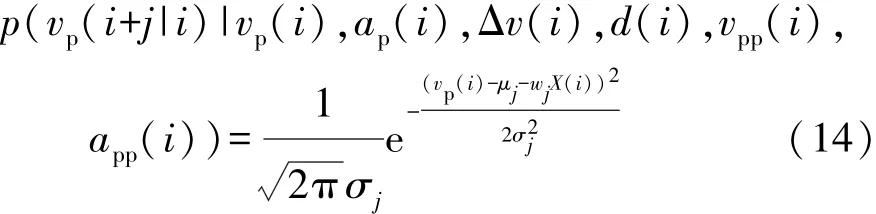
采用最大似然估計對貝葉斯網絡中概率分布參數進行辨識，似然函數為

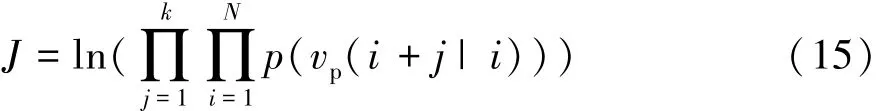
式中：N為樣本容量；k為最大預測步長。對似然函數求極大值，得到貝葉斯網絡概率分布參數：

3 基于貝葉斯網絡的前車狀態預測驗證

本節選用跟車工況下車輛行駛狀態數據中的測試集部分的高速行駛跟車工況數據、低速行駛跟車工況數據和低速到高速行駛的跟車工況數據，檢驗基于貝葉斯網絡的跟車工況下前車運動速度預測效果。標記高速行駛跟車工況、低速行駛跟車工況和低速到高速行駛跟車工況分工況①～工況③，前車狀態預測結果如圖9～圖11所示。

基于貝葉斯網絡的跟車工況下的前車運動速度預測結果分析如下。

(1)由圖9～圖11可知，跟車工況中前車的運動速度均在貝葉斯網絡預測的95%置信區間內，且隨著預測步長的增加，前車運動狀態的不確定性越大，貝葉斯網絡的95%置信區間越大。

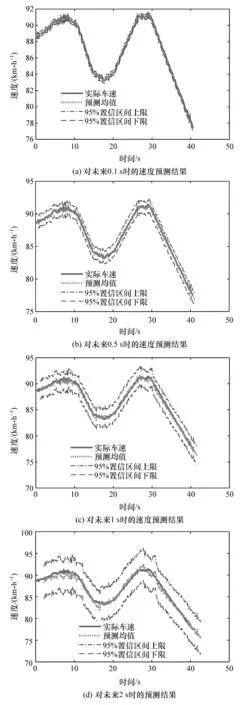
圖9 工況①的預測結果

(2)對比圖9～圖11可知，工況①中前車速度有低頻率的波動，工況②和工況③中前車速度存在稍高頻率的波動。當前車車速以不同頻率波動時，貝葉斯網絡對前車車速預測偏差為：對未來0.1 s時預測車速均值與實際車速偏差的均方根值分別為0.153 6，0.154 0和0.146 6；對未來 0.5 s 時預測車速均值與實際車速偏差的均方根值分別為0.591 5，0.553 9和0.576 3，對未來1 s時預測車速均值與實際車速偏差的均方根值分別為1.154 0，1.062 7和1.095 3；對未來2 s時預測車速均值與實際車速偏差的均方根值分別為2.061 8，1.906 9和1.846 7。因此，由圖9～圖11 3個工況的預測結果可知，當車速存在一定波動時，貝葉斯網絡依然可以在車輛高速行駛的跟車工況、低速行駛的跟車工況和低速到高速行駛的跟車工況中，預測出前車的行駛速度。

4 結論

本文中首先分析車輛跟車工況時運動狀態分布特性，根據先驗知識設計了前車運動狀態預測的貝葉斯網絡，并采用最大似然估計理論對貝葉斯網絡中的參數進行辨識。測試數據顯示前車的實際運動速度均在貝葉斯網絡估計的95%置信區間內，證明了貝葉斯網絡對跟車狀態下前車運動狀態預測能力。多種跟車工況的預測偏差表明了本文中提出的前車運動方法預測效果穩定的穩定性。

后續工作將對前車狀態預測的貝葉斯網絡結構進行研究，進一步提高前車運動狀態預測精度，為車輛巡航控制、節能控制等智能控制方法提供參考。