基于Duffing振子循環檢測方法的研究

楊海博 李 琳

(中國電子科技集團公司第二十研究所 西安 710068)

0 引言

傳統信號檢測方法一般以線性理論為主，即基于時域和頻域分析，如應用廣泛的頻譜分析、Winger-Ville分布、小波分析方法等。這些方法在一定范圍信噪比下，具有良好的檢測性能，但在強噪聲背景下弱信號檢測中卻具有局限性，特別當信噪比低至-10dB附近，傳統線性理論檢測性能急劇下降，甚至難以檢測出待測信號[1]。

近年來，隨著非線性方法在信息科學領域中的深入研究。人們開始將混沌理論用于弱信號的檢測，在對待測信號有一定的預知的情況下，可較為精確的檢測信號幅值、頻率、相位等參數。

頻率是信號的主要參數之一，也是人們常關注對象?；诨煦缋碚摰念l率檢測方法主要有兩種[2]，一種是基于變形的Duffing振子檢測法，另一種是基于Duffing陣法。前者需要對于待側信號頻率有一定的預知，實際應用中常難以對待測信號進行較為精確預知，后者所設置的陣元繁多、計算量巨大，且每個陣元都需要人工尋找系統閾值、誤差波動，工程實現難[3-5]。

針對上述問題,本文在分析了間歇混沌檢測信號頻率的原理，給出了建立較小閾值的混沌系統方法，并引入循環思想，提出了一種計算機易于實現的混沌頻率檢測方法——基于Duffing振子的循環信號檢測方法。

1 Duffing振子檢測原理

Holmes型Duffing方程，其一般數學模型如下[6]：

(1)

式(1)中：rcos(t)為周期策動力；k為阻尼比；-αx(t)+βx3(t)為非線性恢復力。

先調節系統策動力幅值r，使得系統進入混沌運動狀態(如圖1)和大周期運動狀態(如圖2)的臨界狀態，得到閾值rd，再輸入與系統策動力同頻率的待測信號，系統便進入大尺度周期運動狀態，這時調節系統策動力幅值r，使系統再次進入混沌運動狀態和大周期運動狀態的臨界狀態，得到此時的策動力幅值r′，則待測信號的幅值為f=rd-r′。

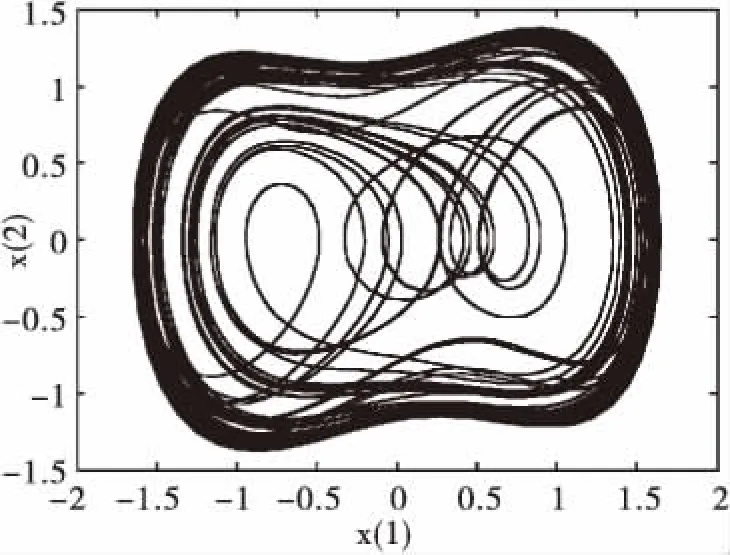
圖1 混沌狀態

圖2 大周期狀態

2 間歇混沌信號頻率檢測分析

Duffing振子系統中引入與其內置策動力之間存在一定的角頻率差的微弱正弦周期信號，即[7]：

(2)

令r=rd，向式(2)系統加入一個任意微弱信號，無論此信號多么小，一定有r+a>rd。假設存在頻差為Δω，系統總策動力為R(t)，則：

=rcost+acostcos(Δωt+θ)-asintsin(Δωt+θ)+n(t)

=[r+acos(Δωt+θ)]cost-asintsin(Δωt+θ)+n(t)

=R(t)cos(t+φ(t))+n(t)

其中：

(3)

(4)

2.1 間歇混沌原理

間歇混沌現象為待測信號與系統策動力存在頻差情況下，出現的特有陣發混沌現象[8]。系統狀態將呈現不同的變化，總策動力R(t)呈現周期變化，具體關系如圖3所示。

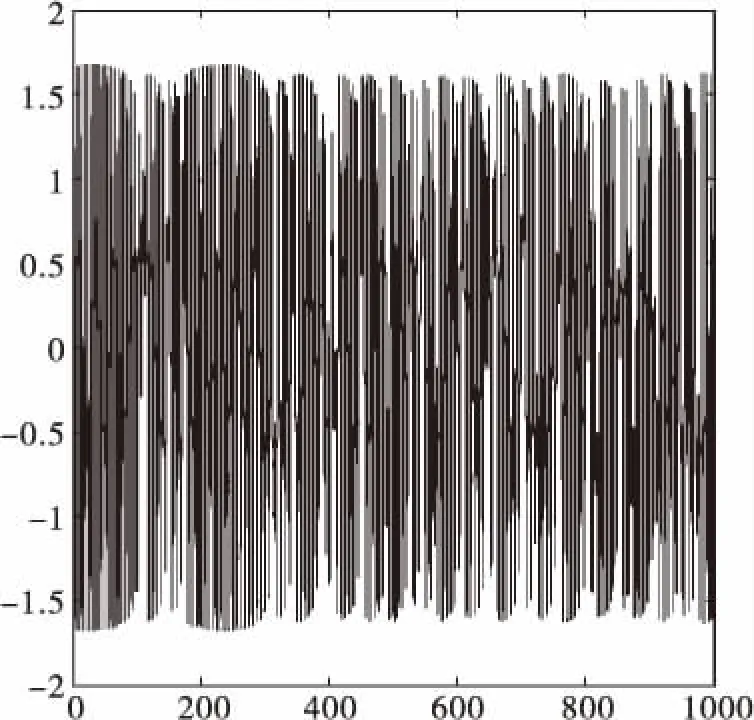
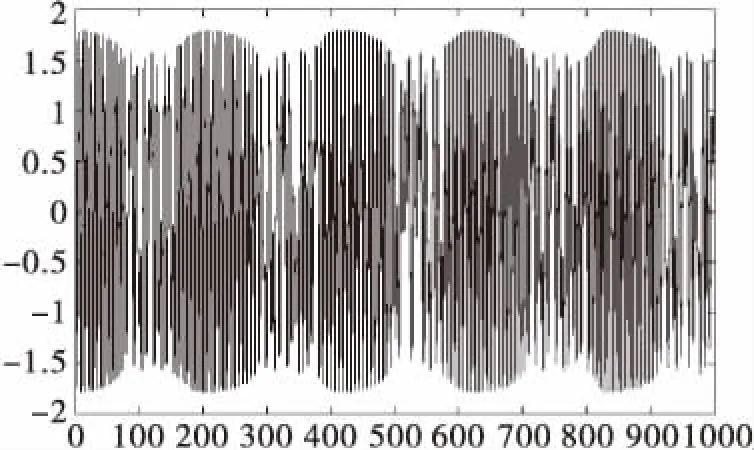
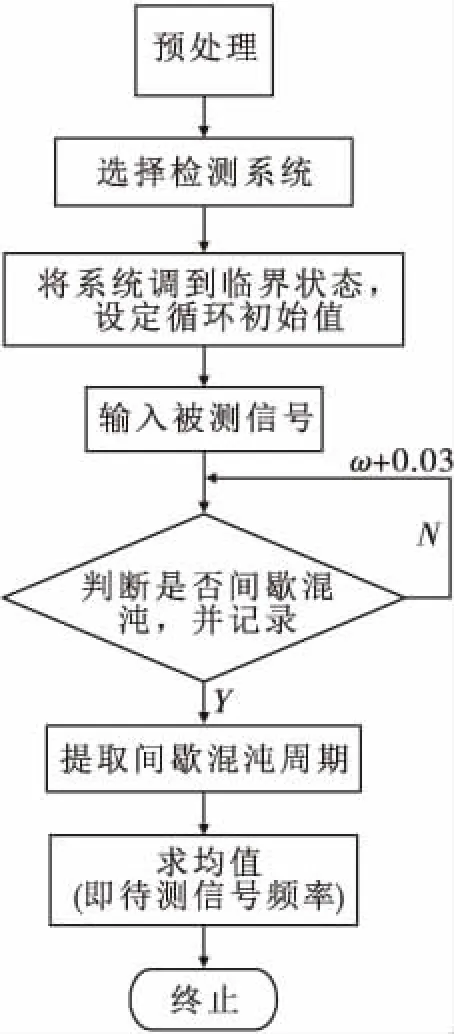
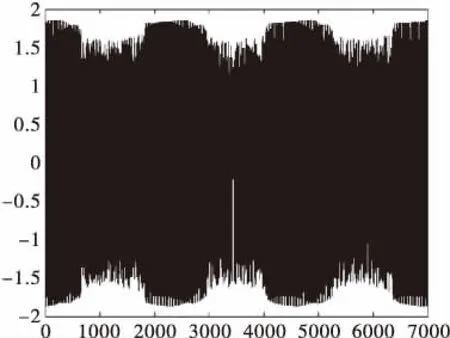
當策動力與待測信號矢量夾角小于90°時，則其合成向量R(t)的幅值就會在某一段大于rd(系統閾值)區域內，系統處于大周期運動狀態；當策動力與外界信號矢量夾角大于90°時，其合成向量R(t)某一段小于rd區域內，即R(t)

與此同時，我主動記下平時不懂的專業知識，遇到相熟的項目經理，抓住碎片時間積極上門請教，不躲閃不回避，主動提及雙方在項目溝通上經常遺漏的部分，強烈表達增進雙方溝通效率的愿望。通過積極主動的溝通，讓項目經理意識到了我個人知識結構上的特點與不足，在后續的工作交流中更加體諒我個人的實際情況。這種互利雙贏的勤學好問，贏得了項目經理的贊許，建立了更加融洽的關系。

由此可見，當策動力與待測信號存在頻率差時，總策動力R(t)周而復始地大于或小于rd，即表現出間歇混沌狀態(在非線性系統中，無論是時間上還是在空間上，間歇的出現混沌的現象，類似于規律性的周期運動)。即系統以一定的周期進行間歇混沌運動，間歇混沌周期：

(5)

2.2 待測信號幅值對間歇混沌的影響

從式(3)可以看出，因racos(Δωt+θ)項影響，總幅值R(t)呈周期性變化。

(6)

當待測信號幅值a遠大于或者遠小于檢測系統閾值r時，式(6)中周期項較非周期項占比η較小，R(t)變化周期較小，即系統難以出現間歇混沌，這表明周期項能量在整個檢測過程中作用較小，難以驅動了檢測系統進入顯著間歇混沌狀態，如圖4所示。

當待測信號幅值a比檢測系統閾值r者相差不大時，式(6)中周期項較非周期項占比η較大，R(t)變化周期較大，即檢測過程中出現顯著間歇混沌現象，這表明周期項能量在整個檢測過程中作用較大，可以驅動檢測系統進入顯著的間歇混沌狀態，如圖5所示。

圖4 混沌振子檢測系統中加入0.01cos(1.03t)時系統時域圖

圖5 混沌振子檢測系統中加入0.1cos(1.03t)時系統時域圖

從以上分析可以看出，但凡基于間歇混沌現象檢測信號頻率，必須保持混沌系統閾值與被檢測信號在一個數量級上或者相差不大，即要檢測微弱小信號，必須選用閾值比較小的混沌系統。

混沌系統。如何建立閾值較小的混沌系統，成為了能否成功檢測到微弱信號頻率的關鍵。

通過多次仿真計算發現，線性系數α越小，閾值也越??；非線性系數β越大，閾值越小，當β=1時，系統閾值與參數α的變化如圖6所示，當α=1時，系統閾值與參數β的變化如圖7所示。

3 基于Duffing振子的循環檢測系統

常規的間歇Duffing陣檢測法存在的主要問題：

1)一般建立陣元數量龐大，不易計算機計算；

3)將間歇混沌間歇周期最大的陣子策動力頻率作為待測信號頻率，誤差較大。

基于Duffing振子的循環檢測系統，剔除了大量陣元的建立，避免了不同的策動力重新設定閾值，采用計算機易于實現的循環算法。

基于Duffing振子的循環檢測法檢測未知微弱信號的步驟如下：

第一步，對待測信號進行預處理，判斷信號頻率數量級，選擇合適的循環混沌檢測系統；

第二步，調節系統處于混沌與大周期狀態的臨界狀態，設定系統循環初始值，選擇策動力頻率循環迭代步長，加載間歇混沌現象記錄程序；

第三步，提取各顯著間歇混沌周期，計算被測信號頻率，并求均值，均值即為被測信號頻率。

圖6 基于Duffing陣子循環檢測系統流程圖

圖7 檢測純信號時，記錄程序記的間歇混沌現象

圖8 檢測帶噪聲信號時，記錄程序記間歇混沌現象

觀察圖9、圖10不難看出隨機噪聲的加入使得原來很光滑的輸出變得粗糙，但未破壞間歇混沌現象，可以明顯看出間歇周期，從而通過軟件程序計算出待測信號頻率。

4 仿真分析

為驗證基于Duffing振子的循環檢測方法性能，本試驗在強噪聲下(信噪比-40dB)，對比新方法與傳統Duffing陣法檢測性能，以及計算速度。

調整Duffing檢測系統基本參數，降低檢測系統閾值，選用與待測信號同一數量級的閾值的檢測系統。

選用k=0.5，α=0.04，β=3000參數，預置系統周期策動力角頻率為1。建立Duffing振子檢測系統：

(7)

經過仿真得到此系統閾值為rd=0.0103。

待測信號模型為：

s(t)=0.01cos(1.09t)+n(t)

(8)

其中n(t)為均值為0，方差為1的高斯白噪聲。

方法1：建立Duffing振子陣，含陣元10，各振元策動力頻率為ω、1.03ω、1.032ω…1.039ω，并將各陣元調至系統混沌到大周期的臨界閾值。

方法2：建立基于Duffing振子的循環檢測系統，循環步長0.03，并設置程序自動記錄(記錄顯著間歇混沌數據)。

圖9 混沌陣第4個陣元的間歇混沌現象

圖10 循環檢測法記錄程序記錄的間歇混沌現象

通過方法1，對各陣元進行仿真計算，發現閾值為0.944的陣元混沌間歇周期最大，如圖11，由式(5)可知，間歇周期越大，檢測系統策動力與待測信號頻率越接近，可認為該策動力頻率就是待測信號頻率。因此認為待測信號頻率為1.0927，檢測誤差為0.25%。

通過方法2檢測，按照圖6流程，提取的間歇混沌現象，如圖12，對于各間歇混沌的周期進行均值處理，均值為1.0901即待測信號頻率為1.0901，檢測誤差為0.09%。且計算速度遠快于方法1。

通過與傳統方法對比不難看出，在-40dB的信噪比下，基于Duffing振子的循環檢測法微弱信號檢測性能優于傳統混沌陣法，且計算速度遠快于方法1。

5 結束語

本文分析了間歇混沌基本原理，推導了待測信號幅值大小對于間歇混沌現象的影響，給出了通過調整檢測系統參數來調低閾值的解決方法，提出了基于Duffing振子循環檢測方法步驟，并對-40dB信噪比下弱信號進行驗證，結果表明新方法檢測精度優于傳統方法。