HPM視野下的高中矩陣教學

辛志立

高中數學中的矩陣教學，是選修的內容，與函數、數列、三角等常駐在高中階段的內容相比，它在高中數學教學中顯得“年輕”而又“份量不足”.

一方面，矩陣帶著“高等數學”的意味，在高中數學內容中相對比較獨立;另一方面，由于其要求并不高，所以出現的矩陣相關題型，難度不大，因為這兩點，很多時候，在進行這一塊內容的教學時，容易形成一種為了考題而教題、學題的狀態，學生對本章節的內容也經常是知其然而不知其所以然，這樣的教法與學法，很難達到教育本身的目的，因為學習數學并不只是學習如何解題，更需要培養學生學習興趣，讓學生獲得數學學科核心素養，提升學生數學思維品質，

因此，試著在HPM視野下進行高中矩陣教學，讓學生從一個更好的角度，對矩陣有一個更全面清晰的認識，所謂HPM即指History and Pedagogy ofMathematics，意為數學史與數學教育，“它不是為了歷史而研究歷史，而是為教育而研究歷史，我們稱之為數學教育取向的數學史研究，其目的之一，是為數學課堂教學提供相關材料，”[1]HPM視野下的高中矩陣教學，就是要在高中矩陣課堂教學中融入數學史，讓學生進一步形成概念、明白原理、理清思路、發展思維.

1 借助數學史，明白數學概念

在HPM視野下的矩陣教學中，我們追本溯源，借助矩陣萌芽的歷史來引入矩陣概念，

早在公元前1世紀，中國的《九章算術》就用到了類似矩陣的東西，以《九章算術》中的一題為例來說：

今有上禾三秉，中禾二秉，下禾一秉，實三十九斗;上禾二秉，中禾三秉，下禾一秉，實三十四斗;上禾一秉，中禾二秉，下禾三秉，實二十六斗，問上、中、下禾實一秉各幾何？

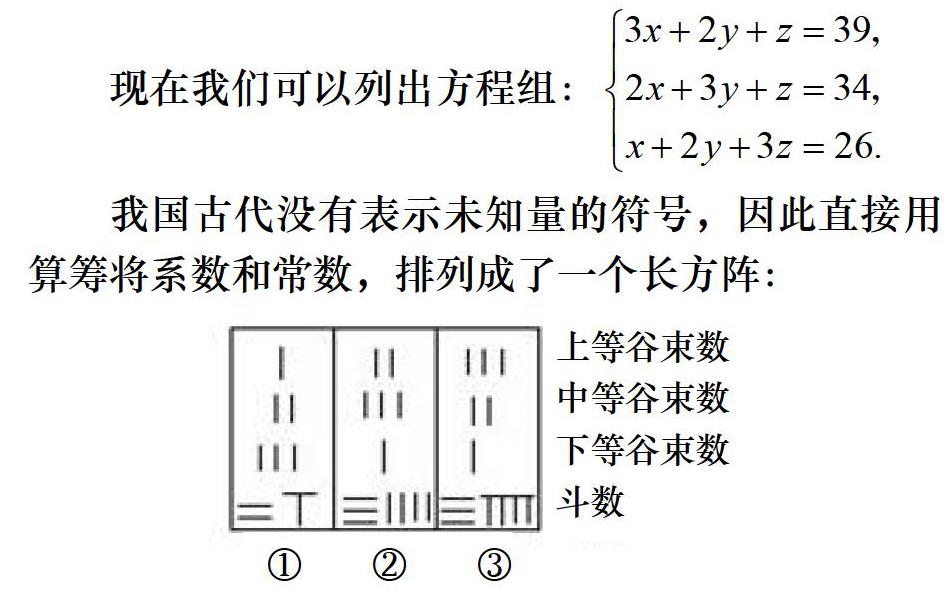
現在我們可以列出方程組：

我國古代沒有表示未知量的符號，因此直接用算籌將系數和常數，排列成了一個長方陣：

這就是矩陣最早的雛形，可以看出，矩陣就是一系列數字（或字母）擺成的陣列，但是它又并不是單純的一種“數學游戲”，而是在古代解決實際問題的研究過程中產生的一種必然形態，

從這樣的數學史介紹引入矩陣概念，提升自豪感并引發興趣固然是原因之一，但是更深層次的作用有三：

（1）得知矩陣因何而來，首先解決了“矩陣是什么”的問題，知道來龍去脈，可以消除新知出現時學生心中的迷惘感，更好的理解概念.

（2）從歷史中找實例，可以得知矩陣并不是數學家們“拍腦門”的舉動，解決了“矩陣有什么用”的問題，從古代的算術中就看到數學工具的實際運用，能讓學生感受到“學以致用”，從而進一步增加學習的興趣.

（3）追本溯源，可以發現矩陣并不是一個獨立的全新的概念，而是與學生的前知緊密相連，因為從矩陣的萌芽歷史可以看到，矩陣就是方程組系數與常數的對應排列，由此可以推知，矩陣與方程組必然有著某些密不可分的關系，可以解決學生對新知的陌生感，同時也能更好地切入下一階段的教學，

“這是什么”和“有什么用”往往是學生接觸新知時最基本的想法，如果能夠較好地解決這兩個問題，那么必然可以讓學生更好地提升學習興趣，產生學習動力，用數學史引進概念，恰恰可以漂亮地做到這一點.

2 利用數學史，滲透數學思想

學生雖然了解了矩陣與方程的密切聯系，但是在學習過程中又引發了新的問題：初中里就已經學會了用消元法解二元一次方程組，并且簡單好用又為自己所熟練使用，現在為什么又要學別的方法來解方程組？而且在學習過程中還需要增加另一個新的概念：行列式，

在這樣的問題下，學生下意識的產生排斥感，往往在學習過程中，有意無意地避開矩陣與行列式，而繼續運用原有的知識來解決問題，

將數學史融入教學，可以有效地解決學生的疑惑，并從中獲得良好的數學思想，

在這個階段，可以利用數學史，進行以下兩方面數學思想的融入：

2.1 程序化思想

在《九章算術》中，利用算籌解出線性方程組的運算過程，是一種按照一定步驟反復操作的過程，整個過程看似繁瑣而復雜，但是卻是一種程序化思想的體現，

在矩陣教學中遇到的解方程組的方法與以前初中時學得的解方程組的方法對比來看，從結構形式上來看，就像《九章算術》中的運算一樣，看上去比較“臃腫”，計算也似乎更為復雜，但是在這里，蘊藏著程序化思想，

我國現代數學家吳文俊就是借助這樣的思想，發明了吳方法，利用程序化的思想，用計算機來解決幾何定理的證明，他說：“由于現代計算機的出現，其所需的方式方法正與《九章》傳統的算法體系相符合，《九章》所蘊含的思想影響，必將日益顯著，在21世紀中必將凌駕于《原本》之上，”[2]

程序化思想的滲透，一方面解決了學生的疑問：為什么已經有了簡單快捷的方式，還需要學習另一個復雜的繁瑣的方式？因為這其中有數學思想的存在;另一方面也提供給了學生一種思維的方向，程序化思想的滲透，有助于學生邏輯能力的提升與思維嚴密性的培養.

2.2 符號化思想

矩陣論的創立者英國數學家凱萊曾說過“矩陣概念，或直接從行列式概念而來，或作為表達線性變換的一個簡便方法而來，”又說：“從邏輯上來說，矩陣的概念應先于行列式的概念，但在歷史上卻正好相反，”可見在歷史的演進過程中，矩陣與行列式幾乎可以看成是一對“雙胞胎”，行列式的表示方式即兩條豎線，就是凱萊在1841年開始使用的，而矩陣的符號，即用以來表示，則是凱萊于1855引入的，

在課堂教學中可以適當地滲透符號化思想，符號化思想其實是一種重要的數學思想，它主要是指有意識、普遍地運用符號去表述研究的對象[3].雖然高中生已經接觸了非常多的數學符號，但是在今后的學習中他們必將接觸更多的數學符號，符號化思想的滲透有助于學生更好地理解數學語言，更好地學習新知，進而讓學生了解到原來創造符號并不是什么難題，更不是數學家才有的“專利”，在一些問題上自己設立一些符號，也許可以事半功倍.

3 串聯數學史，體會數學精神

數學史的滲透，并不是作為一個用一下就拋諸一旁的引入，也不是一個興之所至的即興表演，而是有計劃、有目的的貫穿于整個的矩陣教學的始終，

在高中階段，學生需要學習許多矩陣的初等理論，其中包括了矩陣的相等、矩陣的運算法則、矩陣的逆等，在HPM視野下的矩陣教學過程中，數學課堂不只傳授了對應的知識，也將對矩陣論作出貢獻的日本數學家關孝和、瑞士數學家克萊姆、英國數學家凱萊、希爾維斯特等，一一介紹給了學生，

數學史就像一條蜿蜒可見的絲線，將如此多的知識點一一貫穿起來，讓學生能夠深刻體會到的是：

（1）依傍著歷史看數學，讓學生對矩陣這一塊的知識有一個系統化的認識，很容易在頭腦中形成一條清晰的線索，從而讓所學習的內容不再瑣碎，易記易學.

（2）滲透數學史的學習，讓學生更明白矩陣的本質，明白學習矩陣的作用以及矩陣與其他數學內容間的聯系，進一步形成良好的知識網絡結構，有利于觸類旁通，促進學習.

（3）整個學習過程仿佛是一個歷史縮影，在追隨歷史的過程中，同學們跟隨數學家的腳步，將問題一一解決，讓學生知道每一段數學概念從出現到創立到完善，本身也是一個復雜與曲折的經歷，我們在了解前人創造出歷史的過程中，同樣也接受與理解了他們的思想，同時也培養了自身的探究精神，

“數學課堂不可以為了學數學而學數學，不可以為了考試而學習解題，而應該將一個美麗的數學世界用一個更好的方式呈現給學生，在HPM視野下進行數學教育“可以將學生從數學的孤島上挽救出來，并將他們安置在一個生機勃勃的新大陸上，這個新大陸包含了開放的、生動活潑的、充滿人情味的并且總是饒有趣味的數學，”[4]

參考文獻

[1]汪曉勤.HPM研究的內容和方法[J].數學教育學報，2016.2（1）：18

[2]吳文俊，郭書春.匯校本《九章算術》序[M].沈陽：遼寧教育出版社，1990

[3]王建，程宏.符號化思想與小學數學[J].教育實踐與研究，2006 （10）：41-43

[4]汪曉勤，林永偉.古為今用：美國學者眼中數學史的教育價值[J].自然辯證法研究，2004 （20）： 73-74