開放探究空間開拓數學思維
——《包裝的學問》教學設計與思考（一）

吳志明

【教學內容】

北師大版五年級下冊第80、81頁。

【教學過程】

一、情境創設，由茶的包裝說起

談話引入：茶起源于中國而聞名于世界，茶文化是中國傳統文化的重要組成部分。古人云：“茶亦醉人何須酒，書自香我何須花”。通常家里來了客人，都要給客人泡一杯茶。借用一副對聯：坐，請坐，請上座；茶，敬茶，敬香茶。

師：那我們安慶都有什么茶？

生：岳西翠蘭。

導語：（出示岳西翠蘭的包裝圖片）好茶離不開精美的包裝！包裝可提高茶的品味，提升生活的品質，方便我們攜帶。同學們知道嗎？包裝中蘊含著豐富的數學知識，今天我們就一起來學習這節課。

（板書：包裝的學問）

【設計意圖：數學課堂由茶說起，使學生倍感親切，牢牢扣住了學生的心弦，讓學生在不知不覺之中進入良好的學習狀態。更重要的是茶文化是中國傳統文化的重要組成部分，對學生進行傳統文化教育，是強化學生人文底蘊的一種有效途徑，這恰恰是數學核心素養的一個重要組成部分。】

二、思維之旅，從引導探索開始

●活動一：包裝一盒糖果。

1.出示問題。

師：兒童節快到了，淘氣要給臺灣的小朋友寄一盒糖果，他需要多大的包裝紙呢？（一盒糖果的長為20cm，寬為15cm，高為5cm，接口處不計）

2.理解包裝的含義。

（1）包裝它，就是要包它的哪些部分？（表面）

（2）在實際包裝時，會產生接口，本題是怎么規定的？（接口處不計）

（3）求包裝紙的大小就是求什么？（表面積）

3.計算包裝紙的面積。

教師給出數據，學生口頭報算式及結果。

匯報預測，并板書：

大面 15×20×2=600（cm2）

中面 20×5×2=200（cm2）

小面 15×5×2=150（cm2）

600+200+150=950（cm2）

【設計意圖：此環節通過包裝一盒糖果，喚起學生的已有知識和經驗，從而找到知識的生長點。通過解決問題，讓學生加深對包裝的理解，有利于學生用類比的方法開啟本節課的探索之旅。】

●活動二：包裝兩盒糖果。

1.提出問題。

師：要把兩盒糖果包裝在一起，怎樣包才能節約包裝紙？

（1）學生活動：先想一想，再兩人一組拿出手中的長方體模型擺一擺。

（2）交流反饋。

匯報預測，教師課件演示：

方案①兩個大面重疊

方案②兩個中面重疊

方案③兩個小面重疊

（3）對比：這三種包裝方案，哪種包裝方案最節約包裝紙呢？

匯報預測：第一種，因為第一種重疊的是兩個最大的面。

2.再次提問。

師：大家都認為是第一種方案最節約包裝紙嗎？這只是我們直觀的判斷，數學家在得到一個正確的結論之前，往往要進行反復的驗證，你準備怎樣驗證？（計算三種方案的表面積）

匯報預測：

解題思路一：先算出各個面中長方形的面積，再計算表面積。

方案①：20×15×2+15×5×4+20×5×4=1300（cm2）

方案②：20×15×4+15×5×4+20×5×2=1700（cm2）

方案③：20×15×4+15×5×2+20×5×4=1750（cm2）

解題思路二：兩個長方體表面積之和減去重疊的面積。

方案①：950×2-600=1300（cm2）

方案②：950×2-200=1700（cm2）

方案③：950×2-150=1750（cm2）

解題思路三：根據重合面積越大，減去的面積越多，表面積越小。直接算重疊面積即可。

方案①重疊面積：15×20×2=600（cm2）

方案②重疊面積：20×5×2=200（cm2）

方案③重疊面積：15×5×2=150（cm2）

3.教師追問。

師：通過驗證，確實是第一種方案最節約包裝紙，大家能不能深入思考一下，為什么第一種方案最節約包裝紙呢？

匯報預測：

（師生共同完善）這三種包裝方案，所需包裝紙的面積都是從這兩個長方體的表面積中減去兩個重疊的面，所以，“減去”的面越大，越節約包裝紙。

板書：重疊的面越大，表面積越小。

【設計意圖：策略意識的形成和數學思想的感悟必須貫穿于數學學習的全過程，只有學生親身經歷，感受才會深刻。兩個長方體的包裝方案是本課教學的重點，也是三個、四個或者多個長方體拼擺、包裝的基礎。學生通過動手操作，親身經歷解決問題的全過程。通過經歷探究、思考、表達、歸納的數學化過程，既培養了學生科學、嚴謹的學習態度，又讓學生對策略意識和策略優化認識更加深入，從而把數學的核心素養從根本落到實處。】

●活動三：包磁帶。

1.提出問題。

師：將四盒相同的磁帶包裝在一起，你們能想出哪些包裝方法？（一盒磁帶的長為110mm，寬為70mm，高為16mm）選用哪種包裝方法更節省包裝紙？

（1）分組活動，動手研究。

師：可以先畫出草圖表示你的想法，再在小組內部進行交流。

（2）在作業單上畫一畫，算一算，填一填。

?

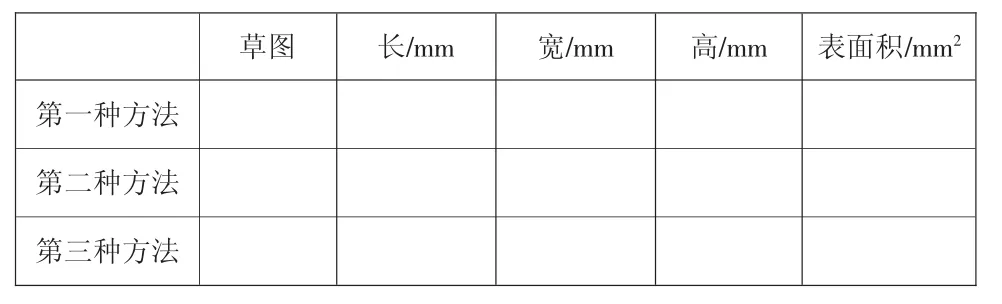
（3）展示交流。

學生展示自己畫的草圖，交流想法，并說出哪個面重疊及重疊面的數量，匯報計算方法和結果（可以匯報優化的策略）。

（4）組織學生比較。

匯報預測：

重疊面：

①六個大面

②四個中面四個小面

③六個中面

④四個大面四個小面

⑤四個大面四個中面

⑥六個小面

最優方案預測：

①六個大面重疊時表面積最小。

②四個大面四個中面重疊時表面積最小。

產生沖突：哪種方案最節約包裝紙？

數學思考：重疊面種類與數量各不相同，怎么比？通過引導、思考、辨別發現：最優方案產生于方案①、⑤之中，這只需比較兩個大面面積之和與四個中面面積之和的大小，也就是一個大面面積與兩個中面面積之和之間的大小，進而達到策略的優化。

（5）得出最優方案：方案①最節省包裝紙。

2.總結反思。

師：通過上面的活動，你有什么體會？

匯報預測：

包裝時盡量“減少”面積最大的面，就越節約包裝紙……

3.小結拓展。

（1）生活中像這種多個相同長方體疊放是否一定都是大面重疊最節約包裝紙呢？四個大面四個中面重疊時表面積有可能比六個大面重疊大嗎？

匯報預測：當兩個中面合并在一起面積比一個大面大時。

課外練習：如果把磁帶盒的高改為40mm，長和寬不變，你有什么發現呢？把你的研究成果寫成數學小論文，明天交給老師。

（2）在實際生活中，有時需要考慮美觀、便于攜帶等因素，無需考慮節約包裝紙的問題。課件出示實例（略）。

【設計意圖：教學中教師努力為學生提供一個自由發展的舞臺，在學生產生認知沖突后，把探索的權利交給學生，把展示的空間讓給學生，讓學生帶著問題進行小組活動，提高了小組活動的有效性。通過擺一擺、畫草圖等探究活動，進一步發展學生的空間觀念和探究能力，把核心素養落到實處。通過適時拓展從而使《包裝的學問》的課題內容更加豐富，內涵更加完整。】

三、全課總結，在反思展望中結束

師：通過這節課的學習你有什么收獲？對自己或他人在這節課的表現有什么要說的？

小結：今天通過“猜想——探究——驗證”的方法學習了《包裝的學問》一課，發現了小小的包裝里面還蘊藏著這么深的學問。探索了多個相同長方體疊放后使其表面積最小的最優策略。