基于貝葉斯理論的云模型參數估計研究

高艷蘋，呂王勇，王玲玲，蔡琳芝

（四川師范大學 數學與軟件科學學院，成都 610068）

0 引言

云模型由三個云參數期望Ex、熵En、超熵He構成，并且自1995年由李德毅院士提出至今有著十分廣泛的應用，包括智能控制[1]、數據挖掘[2,3]、多屬性決策[4,5]和分析評價[6]等。這些應用領域大部分將精確的數量值變為定性的語言值，這種轉換最關鍵的部分就是通過精確的數量值估計出云參數值。經典的云參數估計方法有矩估計法和極大似然估計法，二者的共同點是在將樣本均值作為期望估計值的前提下，分別求得熵、超熵的矩估計和極大似然估計。在期望不是一個未知參數，而是一個隨機變量，且分布已知的假設下，應用貝葉斯理論，得到期望的后驗分布及其后驗估計，然后通過期望的后驗估計求得熵、超熵的后驗矩估計和后驗極大似然估計。貝葉斯理論在云模型中的應用除此之外還包括：空戰態勢評估[7]、空中目標威脅評估[8]、公路物流供應鏈整體協調[9]、航空發動機性能評估[10]等。

本文將Ex作為一個隨機變量，根據其先驗分布推得其后驗分布與后驗估計；再根據Ex的后驗估計得到關于En、He的后驗矩估計和后驗極大似然估計；最后運用均方誤差準則，通過仿真實驗對這幾種估計方法加以比較，得到后驗的極大似然估計法效果最優的結論。

1 云模型

1.1 云模型的定義及基礎知識

云是利用自然語言值表示的某個定性概念A與其定量表示之間的不確定性的轉換模型。設U是一個用精確數值表示的論域，A是U上對應的定性概念，對于任意的x∈U，都存在一個[0，1] 區間上具有穩定傾向的隨機數μA(x)，μA(x)叫做x對A概念的確定度，x在論域上的分布稱為云模型，簡稱為云。云由數字特征期望Ex、熵En、超熵He來反映定性概念整體上的定量特征[11]。期望Ex是整個論域的重心，也是概念量化的最典型樣本；熵En是概念A不確定性的度量，熵越大，概念越宏觀，模糊性和隨機性也越大；超熵He是熵的不確定性度量，即熵的熵。云將定性概念的整體特性用三個數字特征值來定量反映，對理解定性概念的內涵和外延有著極其重要的意義，而且通過三個數字特征，可以設計不同的算法來生成云滴及其確定度，得到不同的云模型[11,12]。

在云模型中，兩個最關鍵、最重要的算法是正向云算法[11]和逆向云算法。正向云算法是在已知云模型的三個參數Ex、En、He值的情況下，產生帶有確定度的云滴樣本。逆向云發生器是根據一定數量的云滴樣本得到表征定性概念的三個參數Ex、En、He的值。兩種算法綜合應用，共同實現定性語言值與定量數值之間的自然轉換。

由于正態云的普適性[12]及其在云模型中的重要地位，所以本文主要研究正態云模型。在正態云中，設X是一隨機變量，且X～N(Ex，y2)。

其中：

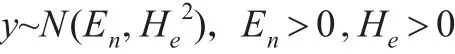
則y的概率密度函數為：

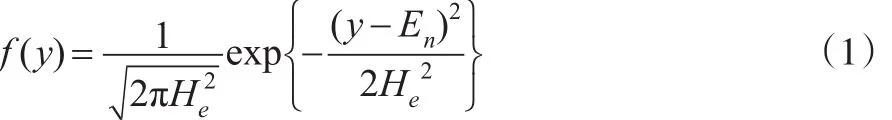
當y為定值時，X的條件概率密度函數為：

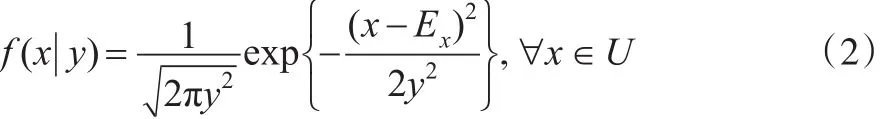
根據式（1）和式（2），又由條件概率密度公式[13]，可知X的概率密度函數：

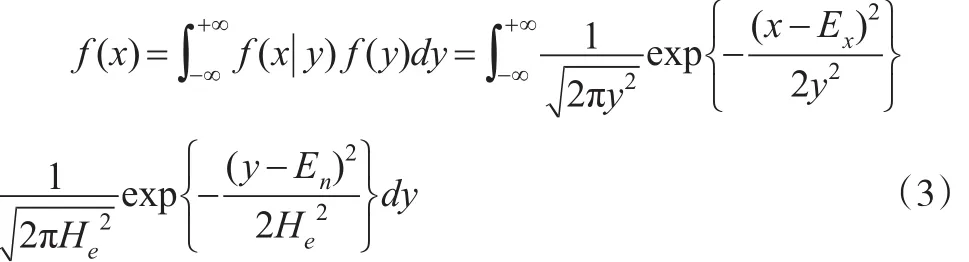
由此可得[14,15]：

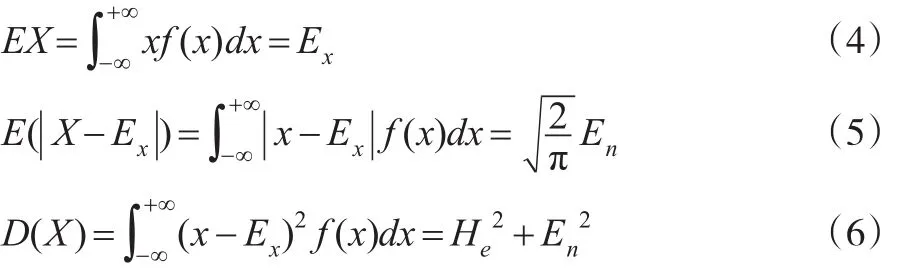
1.2 云滴的產生過程

云滴的產生過程如下：

（1）生成期望值En、標準差He的正態隨機數y；

（2）生成期望值Ex、標準差y的正態隨機數x；

產生云滴之后需要將這些云滴送入云滴檢驗器，通過檢驗的云滴才可以使用。

1.3 云滴檢驗器

（1）因為云滴服從N(Ex，En2+He2)的正態分布，由中心極限定理知，當時，定型概念的確定度可以達到1-α，其中為標準正態分布的雙側百分位點。計算出的云滴點的均值XL和的云滴點的均值XH。當滿足時：其中d=XH為在給定α時定性概念覆蓋達到1-α的范圍，則可認為云滴聚集度較高，即專家意見差異較小，可以接受，若不符合，需要修正[16]。

（2）將置信范圍1-α之外的云滴去除，利用初始的Ex、En、He重新生成等量的云滴。

（3）將新生成的及沒被剔除掉的云滴樣本，運用矩估計[15]，得到新的參數Ex、En、He的估計值。

有了樣本并且對樣本進行了檢驗，通過檢驗的樣本就可以進行云參數的估計，下面介紹兩種經典的云參數估計方法。

2 經典的云參數估計方法

2.1 云參數的矩估計

設x1，x2，…，xn是來自隨機變量X且通過檢驗的一簇云滴樣本，根據式（4）至式（6）并結合樣本求得云參數的矩估計如下：

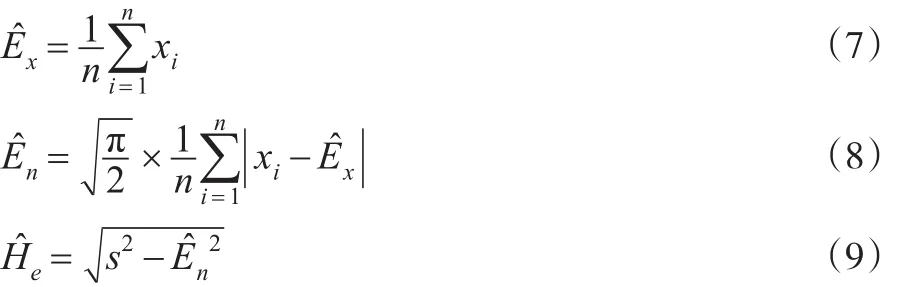
2.2 云參數的極大似然估計

沿用上面的假設，x1，x2，…，xn是來自X并且通過檢驗的一簇云滴樣本，X～N(Ex，y2)，y～N(En，He2)。因為云模型共有三個未知參數，其中樣本均值是參數Ex的無偏估計，所以在這里參數Ex的估計值依舊使用樣本均值代替，即由式（3）知X的密度函數為：

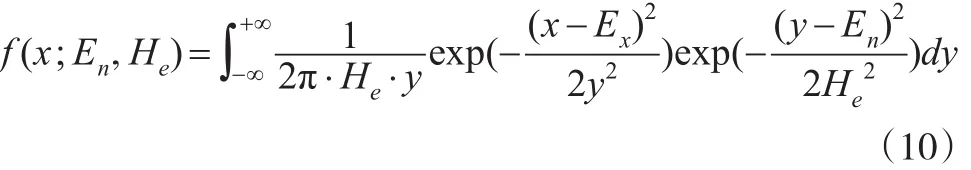
所以這組樣本點的似然函數為：

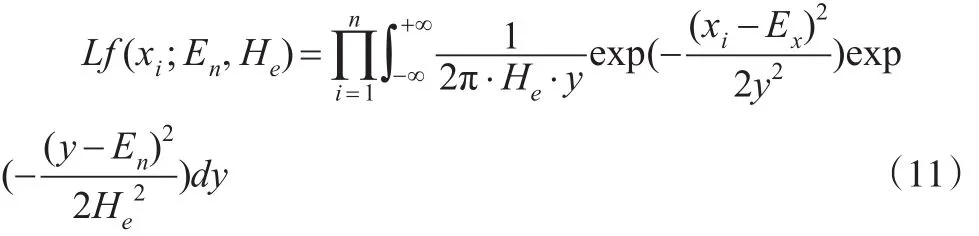
記：

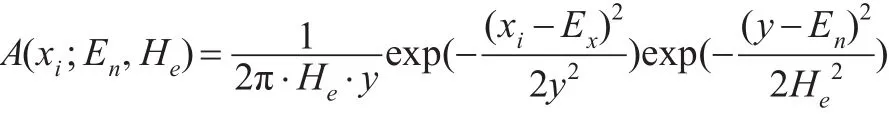
將式（11）取對數，得到：

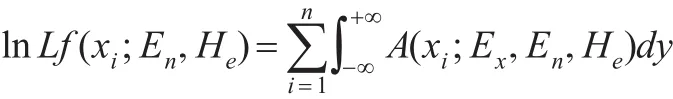
然后將式（11）分別對He，En求導，得到：

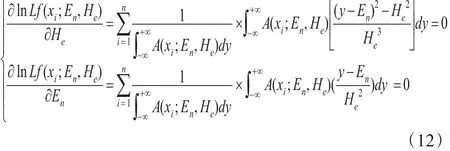
滿足式（12）的解就是En，He的極大似然估計。

不管是矩估計還是極大似然估計，在對參數Ex進行估計時都是用的樣本均值。假設Ex不是一個未知參數，而是一個隨機變量，并且知其先驗分布，那么就可以應用貝葉斯理論得到Ex的后驗分布，下面給出Ex的后驗分布推導過程及參數的后驗估計。

3 云模型中Ex的后驗分布與參數的后驗估計

3.1 Ex 的后驗分布

設x1，x2，…，xn是來自X并且通過檢驗的一簇云滴樣本，其中En，He是未知參數。假設Ex的先驗分布服從正態分布，這里的c0表示Ex的期望，是Ex的方差，可得樣本X的分布和Ex的先驗分布分別為：

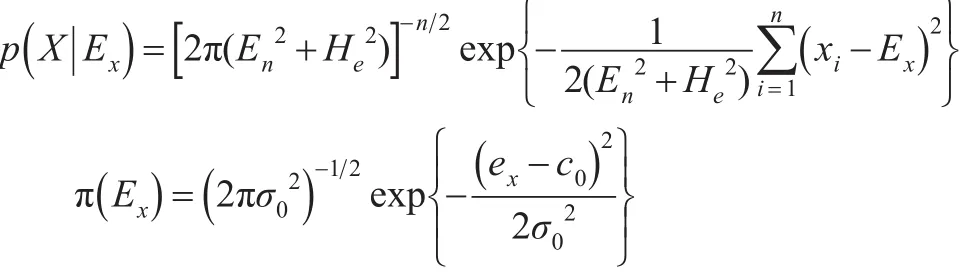
由此可以寫出X和Ex的聯合分布：

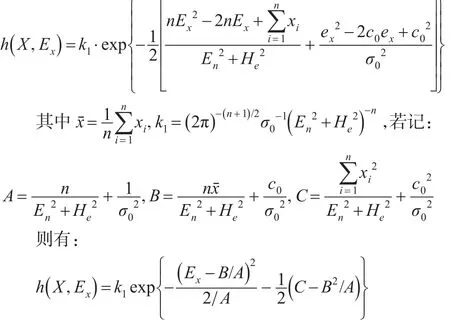
可見A、B、C均與Ex無關，由此容易算得樣本的邊際密度函數和Ex的后驗分布：

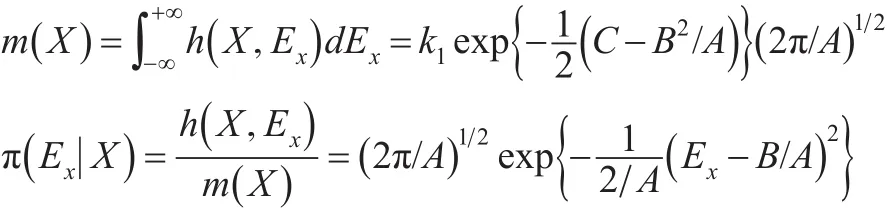
這說明在樣本給定后，Ex的后驗分布為,即：

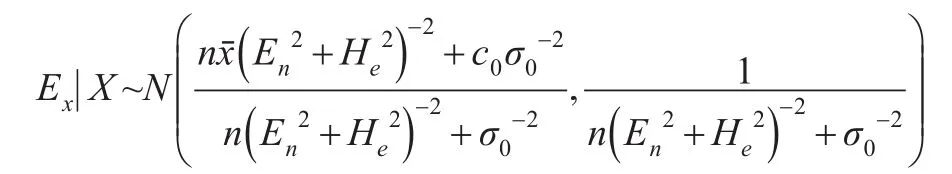
后驗分布的均值即為Ex的后驗估計，記為

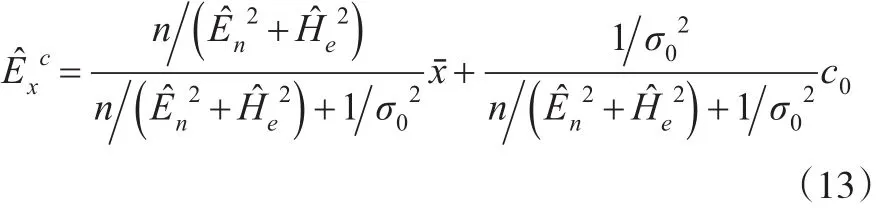
其中，是En，He的矩估計。有了Ex的后驗估計就可以得到參數En、He的后驗矩估計和后驗極大似然估計。

3.2 En、He 的后驗矩估計

公式（13）是Ex的后驗估計，再根據式（5）和式（6）得到En、He的后驗矩估計為：

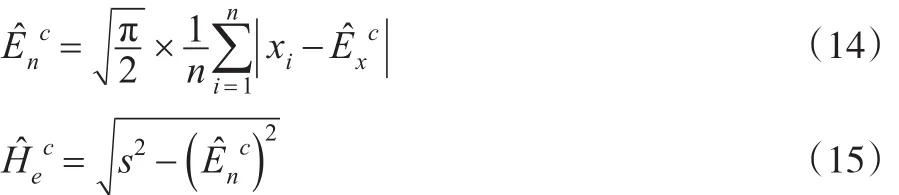
其中s為云滴的樣本標準差。

有了Ex的后驗估計，也可以據此構造參數En、He的后驗極大似然估計。

3.3 En、He 的后驗極大似然估計

上文給出了求得En、He極大似然估計的方法，后驗的En、He的極大似然估計法與其原理相同，唯一不同的是，經典的En、He極大似然估計所使用的Ex的值是由樣本均值代替的，后驗的En、He的極大似然估計所使用的Ex的估計值是通過貝葉斯理論得到的，將Ex的后驗估計值帶入到公式（12）中，求得滿足方程組的解就是En、He的后驗極大似然估計。

4 仿真

無偏性是對估計量的一個重要而常見的要求，但是很多時候無偏估計是不存在的，也不一定比有偏估計更優。從直觀上理解，一個好的估計應該在真值周圍波動，同時擁有較小的均方誤差，所以均方誤差也是一個評價估計優劣的有力標準。本文用均方誤差綜合評價估計的優劣。

設初始云參數為Ex=25，En=3，He=0.1，并用此組值產生云滴樣本。剔除掉隸屬度大于99.99%的樣本點和偏離很大的云滴樣本，然后等數量取樣，將重新得到的云滴加上沒被剔除的云滴送入到云滴檢驗器進行檢驗云滴，檢驗通過的云滴樣本進行計算。根據云滴樣本容易求得經典的云參數的矩估計值；在使用經典的云參數的極大似然估計方法時，由于式（12）是無窮積分，所以根據6σ原則[13]，將無窮積分變為定積分，利用復合梯形求復雜定積分的方法計算式（12）中的每一個積分，而后將En、He設定區間和步長，每取一次En、He的值，帶入到計算后的積分中，找到使式（12）結果最接近0的En、He的值，那么這組En、He即為所求。

在求Ex的后驗估計時，En、He的值是已知的，即為參數En、He的矩估計值；然后根據求得的Ex的后驗估計得到了En、He的后驗矩估計。En、He的后驗極大似然估計就是將式（12）中Ex的值用Ex的后驗估計值代替，其余的求解方程組的步驟與經典的極大似然估計求解步驟相同，最后得到的使式（12）結果最接近0的En、He的值就是En、He的后驗極大似然估計。

四種算法下熵En和超熵He的均方誤差比較如下頁圖1和圖2所示。

圖1是四種算法下熵En均方誤差的比較。由圖1可知，經典熵的矩估計的均方誤差最大，熵的后驗極大似然估計的均方誤差最小，所以四種算法中熵的后驗極大似然估計算法效果最優。參數的矩估計隨著樣本量變化的增加波動較大，而極大似然估計的波動較為平緩，且極大似然估計的均方誤差要小于矩估計的均方誤差，所以極大似然估計法的估計效果比矩估計法要好。在兩種極大似然估計算法中，后驗的熵的極大似然估計的均方誤差最小，說明其效果最優。

圖2是四種算法下超熵He均方誤差的比較。由圖2可知，經典超熵的矩估計的均方誤差最大，超熵的后驗極大似然估計的均方誤差最小，所以四種算法中超熵的后驗極大似然估計算法效果最優。參數的矩估計隨著樣本量變化的增加波動較大，而極大似然估計的波動較為平緩，且極大似然估計的均方誤差要小于矩估計的均方誤差，所以極大似然估計法的估計效果比矩估計法要好。在兩種極大似然估計算法中，后驗的超熵的極大似然估計的均方誤差最小，說明其效果最優。

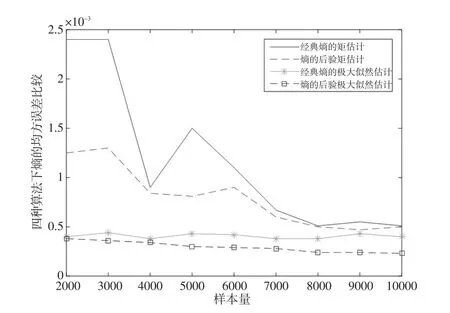
圖1 四種算法下熵En均方誤差比較

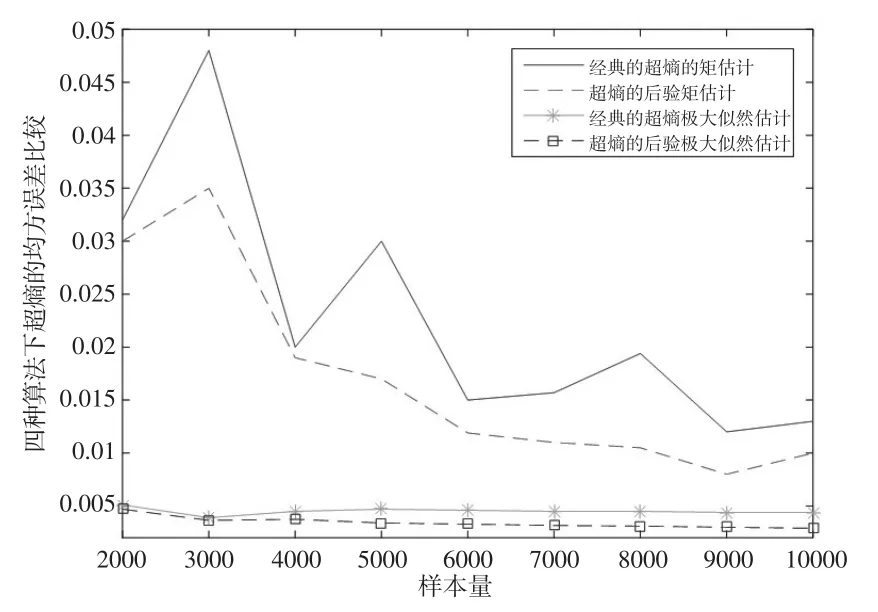
圖2 四種算法下超熵He均方誤差的比較

5 結束語

本文主要研究了云參數的估計方法，在經典參數估計的理論基礎上，應用貝葉斯理論得到了后驗的參數估計方法，并將經典的參數估計法與后驗的參數估計法加以比較，得到了后驗的極大似然估計效果最優的結論，所以在今后估計云參數時應使用后驗的極大似然估計法以使云參數值更加準確。