高中數學教學中運用數形結合提高解題能力的實踐與研究

◎楊軍祥

引言：眾所周知，數學方法在高中數學教學中是很重要的。數學方法包含函數與方程方法、分類討論的方法、轉化與劃歸的方法以及數形結合的方法四大類基本思想方法，它們不僅在高中數學中發揮著自己獨特的作用，有時也能應用到實際生活中，所以教師與學生應更加注重思想方法的學習。

一、數形法合方法概述

高中數學知識是抽象的，復雜的，邏輯性強，學生學習難度較大。數形作為數學知識學習中的主要元素，主要涉及有定量關系和空間圖像。在特殊情況下，定量關系可以轉化為空間圖形，空間圖也可以轉化為定量關系，力求復雜問題簡單化，幫助學生解決問題，提高學習效果。數形結合思想方法在數學知識學習中，將數學圖像轉變為數學語言，有機整合抽象思維和形象思維，解決抽象性問題，在加深知識理解和記憶的同時，有效提升學生的解題能力。在高中數學學習中，應遵循雙向原則和等效原則。主要是在對幾何圖形進行分析時，要考慮到代數抽象的分析，充分發揮代數語言的邏輯特征，避免集合直觀思維的約束，提高學習效果；等價性原則則是要求在數字和圖形相互轉變中，保持等價關系，究其根本在于部分圖形自身局限性，畫圖中無法把握精準性，可能影響到解題效果，所以需要注重數字和圖形的等價。

二、數形結合在高中數學教學中的作用

1.數形結合有利于學生形成系統的知識框架 當學生進入高中階段，數學知識變得更加抽象復雜，且大部分內容采用的是文字的表述方式，容易使學生感到學習枯燥乏味，從而不能夠很好的理解知識，但是教師在既能利用數字或符號也能利用圖形教學時，如果將兩者相結合來授新課或講解習題，則能夠幫助學生更好的掌握和記憶所學的知識，也有利于學生自己認識到知識或問題的根本，這樣有助于學生形成系統的數學知識框架，逐步實現知識從感性到理性的認識和轉變，即可加深對數學知識的理解。

2.數形結合有利于拓展學生的思維 數形結合就是將數學中籠統的數學語言、數學符號和繁雜的數量關系與形象直觀的圖形相互轉化，將抽象思維與形象思維有機結合，借助形的直觀反映數量之間的關系，借助數的具體描述形的內涵。在使用這一方法進行相互轉化的過程中有利于培養學生的直觀思維和發散思維，則可拓展他們的思維廣度，且在對具體問題進行深入研究剖析中，可以培養他們解題思維的獨創性、準確性、廣闊性以及靈活性等。

3.數形結合有助于提升學生的美學素質 高中數學雖然整體上來說是抽象的，但其中依然存在許多種形式的美，如三角函數公式的輪換美，圓圖形的和諧美，直線的簡潔美，橢圓雙曲線的對稱美以及各種奇異美等等，因此在教學活動中教師滲透數形結合方法，學生應用數形結合方法，不僅可以讓學生發現和感受數學的唯美，還可以使學生的審美意識得到提高，學生的審美情操得以培養，學生的審美動力得以激發，學生的審美熱情得以洋溢，還能調動學生學習數學的積極性，即學生自己主動想在學習中發現美，體會美，進而創造美，這樣不僅使學生學到了知識，而且也能提升他們的美學素質。

三、數形結合教學過程中教師教學的所采取的策略

1.克服學生心理因素，提高學生學習興趣 學習過程中，學生只有在具備對學科學習興趣的基礎上才能夠將全身心的精力投入到學習的過程中。所以教師在教學過程中需要不斷激發學生在學習過程中的新鮮感。同時，教師在教學過程中還需要借助多媒體設備來激發學生在學習過程中的注意力，學生在擁有了學習興趣以后也能夠拿起畫筆，當在數學學習過程中遇到需要利用圖像解決為問題的時候就能夠拿起畫筆進行畫圖。這樣學生在解決自身問題的過程中也能夠不斷提升對數學學習的自信心。同時，教師還需要了解學生對知識的掌握程度，這樣才能夠做到有的放矢，提升數學教學質量。

2.充分利用現代化教學手段，提升學生形象認知 現代教育過程中，現代教學手段打破了傳統教學中的黑板與粉筆的教學模式，這樣也能夠在現代化教學手段的影響下掃除傳統教學過程中存有的教學弊端，使得枯燥抽象的學習內容更加形象化，尤其是數形結合思想在圖形的講解以及變化過程中。在解題過程中若在多媒體課件中演示則更易被學生接受和理解。這樣，不僅增強了學生學習數學的興趣，活躍了學生的思維，讓學生一節課有多個興奮點，還可以使教材和媒體之間優勢互補。多媒體教學新穎活潑的形式不但能激發學生的學習熱情，而且引導學生主動學習，從而形成一個良性循環的學習過程。它集文字、聲音、圖像和動畫于一體，生動直觀，還能創設教材難以提供的情景，體現多媒體的綜合效果，改善教學環境，優化教學結構。

3.將數轉形 圖形具有強大的形象性。與數學語言相比，它具有顯著的優勢。因此，在高中數學教學中，你可以使用數形結合法將一些抽象的，難以解決的代數問題轉化為圖形問題，這樣就可以開闊學生的思維，及時找到正確的解決方法，從而有效地改善學生解決問題的能力。在探究函數零點個數或者方程求解的過程中，教師可以使用數形結合方法來回答問題，這樣有助于激發學生解答問題思路并幫助他們快速解決問題。同時，通過顯示視覺圖形，可以培養學生觀察問題的能力，促進學生思維能力的擴展。例如數形結合在集合教學過程中的應用。有三個集合 A，B，C（不必相異），它們的并集是 AUBUC＝｛1，2，…，10｝，求滿足這一條件的集合的有序三元組（A，B，C）的個數。分析：此題若直接從統計角度計算，首先就得分三類：（1）A，B，C都不一樣；（2）A，B，C都一樣；（3）A，B，C中兩者一樣。在三種情況中，A，B，C都相同則可以直接畫樹狀圖或者列表格進行統計，但另外兩種情況還需繼續分類討論，且要對三個集合中元素的個數也要分情況討論，總體情況比較繁多，所以很容易多算或者漏算，極易出錯，但若從Venn圖角度出發，問題會變得一目了然，清晰直觀。

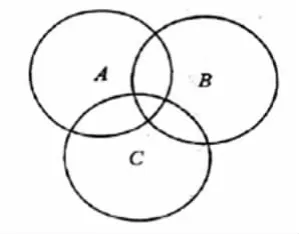
從圖可知求AUB UC時，因為三個集合AUB UC之間交出了7個區域，從而1，2，…10中每個數都有7種選擇。故所求有序三元組（A，B，C）的總個數為7。

4.加強專項訓練，培養學生的數學核心素養 教師應當加強對學生數形結合專項訓練，利用不同題型以及不同難度的問題對學生進行有針對性的講解，這樣也能夠讓學生在練習的過程中理清解題的思路，深入理解數形結合思想，并且能夠對做題的成果進行不斷的鞏固。只有多練多講，才能反復提升學生的能力，提升其數學核心素養。數學核心素養包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析等。每一個核心素養之間是相輔相成，有著千絲萬縷的聯系。數形結合的思想方法只是巨大數學知識網絡中的一環，這一環打通，往往會觸類旁通，起到事半功倍的效果。

結語：總之，高中數學教學過程中要將數形結合思想進行更加透徹的了解，在實際的教學過程中，教師需要能夠將“數”與“形”之間進行有機的結合，激發學生在學習過程中思考的積極性，充分調動學生學習的積極性，在提高學生解題能力的同時，還可以保證解決問題的正確率.通過數形結合解題思想的整合運用，使學生形成清晰的解題思路，提高解題效率，促進學生的全面發展。