淺談圓錐曲線的第三定義及運用

◎楊麗

新課程數學教學，實現的是學生對所學知識的螺旋式上升。在新授課過程中，對選修2－1第41頁例3“設點A，B的坐標分別為(－5，)0，( 5，0).直線AM，BM相交于點M，且它們的斜率之積是，求點M的軌跡方程.”，僅僅是對用直接法求軌跡方程的應用。但在高三一輪復習中，學生的認知能力全面提升，在復習到橢圓時，應重溫此例，并對其拓展到橢圓的第三定義，適時擴充到雙曲線的第三定義，并加以應用。

一、橢圓的第三定義

證明：以焦點在軸上的橢圓為例，構造△PAB的PA邊所對的中位線MO，kPA＝kMO

二、雙曲線的第三定義

證明：只需將橢圓中的b2全部換成－b2就能將橢圓結論轉換成雙曲線的結論。

三、簡單運用例題

（1）若直線l1：y＝k1x＋1與直線l2：y＝k2x－1的交點在橢圓2x2＋y2＝1上，則k1k2的值為_________.

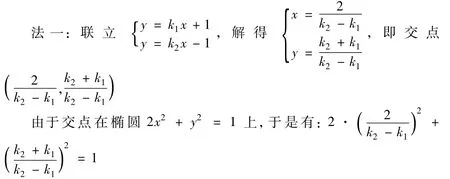
化簡得：k1k2＝－2

法二：直接利用橢圓的第三定義，交點視為點P

則k1k2＝－2

點評：從以上兩種解法可以看到：法一完全體現解析幾何的“本色”——運算，平鋪直敘，一氣呵成，但計算量較大，易計算容易出錯；法二直接利用橢圓的第三定義解題，省去繁瑣的計算，提高效率。

點評：兩頂點一動點的模型聯想到第三定義，那么剩下的任務就是把題目中的角轉化為兩直線的傾斜角，把正余弦轉化為正切。而題目中的正余弦化正切是三角函數的常見考點。

點評：在此法中，合理利用M、N的對稱關系是解題的關鍵，這樣可以利用橢圓的第三定義將兩者斜率的關系聯系起來，既構造了“一正”，又構造了“二定”，利用基本不等式“三相等”即可用a、b表示出最值1。

四、能力提升練習

（1）已知雙曲線C：x2－y2＝2019的左、右頂點分別為A、B，P為雙曲線右支上一點，且∠PAB＝4∠APB，則∠PAB＝______.

可見，在解題中，要落實到定義，它是一切后繼知識應用的牢固根基。要想準確運用好橢圓、雙曲線的第三定義解題，在審題中，抓住曲線上關于原點對稱的兩點，斜率等關鍵詞是快速入手的關鍵。