考慮共因故障的系統組成單元故障嚴重性測度模型

曹穎賽 劉思峰 方志耕 董文杰

南京航空航天大學經濟與管理學院，南京，210016

0 引言

共因故障是指由于空間、環境、設計以及人為等方面的共同原因所造成的多個部件同時發生故障的現象，是一種廣泛存在于工程系統中且在系統設計、制造、安裝、運行的任何階段都會發生的相依故障事件[1-3]。在共因故障中，受共同原因影響的部件集合稱為共因部件組。

共因故障增大了系統各單元的故障概率，降低了采用冗余配置提高系統可靠性的效果。隨著單部件級可靠性的大幅度提升和冗余技術的應用，這種由多部件相關故障引起的系統可靠性退化甚至安全隱患問題日益加劇，促使了大量系統分析人員和學者相繼投入到共因故障影響下的系統可靠性研究中。李春洋等[4]提出了一種考慮共因故障的多態系統可靠性優化模型，為復雜系統的可靠性冗余配置優化問題提供了較完整的解決方案。針對大部分包含共因故障的系統可靠性分析模型缺乏考慮共因故障動態特征問題，王家序等[5]基于動態故障樹對包含不完全共因故障的系統可靠性進行了建模分析。

上述研究側重于解決共因故障的表征、發生概率求解以及相關性解析等問題，有關共因故障的嚴重性測度問題還有待進一步研究。作為產品全壽命周期中的關鍵測度指標，故障嚴重性是指某一故障模式對系統功能、用戶人身安全以及周圍環境等方面的影響程度，是識別產品各種缺陷與薄弱環節的基礎。在故障模式、影響及其危害性分析(failure mode effect and criticality analysis，FMECA)過程中，故障嚴重度還可以用于確定故障風險優先序數(risk priority number, RPN)和故障危害性分析(criticality analysis, CA)。文獻[6]從消除故障所需付出的努力程度視角定義了故障嚴重度，使其能夠更真實、定量地反映系統及其組成單元的故障嚴重性。文獻[7]將武器裝備的故障嚴重度劃分為4個類別，旨在定性地區別武器裝備的各個故障模式。文獻[8]以等級表的形式對指揮、控制、通信、計算機、情報、監視和偵察系統的故障嚴重性進行了測度，然而該方法只是定量地表征故障嚴重度，難以確切表征不同嚴重度故障之間的區別。文獻[9]針對上述測度方法的缺陷，提出了一種故障嚴重度非線性轉換函數，解決了不同故障在嚴重度方面的各類運算問題。文獻[10]針對文獻[9]中的指數型故障嚴重等級非線性轉換函數無法反映故障之間的關聯性問題，提出了一種基于Copula函數的3階轉換方程。

上述故障嚴重性測度方法與技術僅針對系統組成單元(或子系統)的單一故障，對系統中的共因故障難以為繼。無法回避的是，在共因故障的影響下，在系統組成單元單一故障所造成的危害性后果基礎上，勢必還會出現由單元故障間的關聯性所導致的額外嚴重性危害。如果繼續按照以往的方法對系統組成單元故障進行嚴重性測度，則會低估單元故障的嚴重性，從而導致后續的故障消除資源配置結果出現偏差，影響系統運行效率。由此，在共因故障存在的條件下，探索新的故障嚴重性測度模型與方法勢在必行。

本文基于合作博弈思想構建考慮共因故障影響的系統組成單元故障嚴重性Shapley值測度模型。在模型構建過程中，系統組成單元被看作是合作博弈中的參與主體，共因部件組則是博弈過程中形成的聯盟。首先，在已有故障嚴重等級測度的基礎上，構建最優非線性轉換函數；其次根據共因故障特征提出其聯合嚴重性測度方法；最后在確定共因部件組數量和種類的基礎上求解單元故障修正嚴重度，即系統組成單元對各個共因故障聯合嚴重度的期望貢獻度。

1 故障嚴重性測度

1.1 單一故障嚴重性測度

根據文獻[8]，系統組成單元(或子系統)單一故障的嚴重程度可分為表1所示的10個等級。

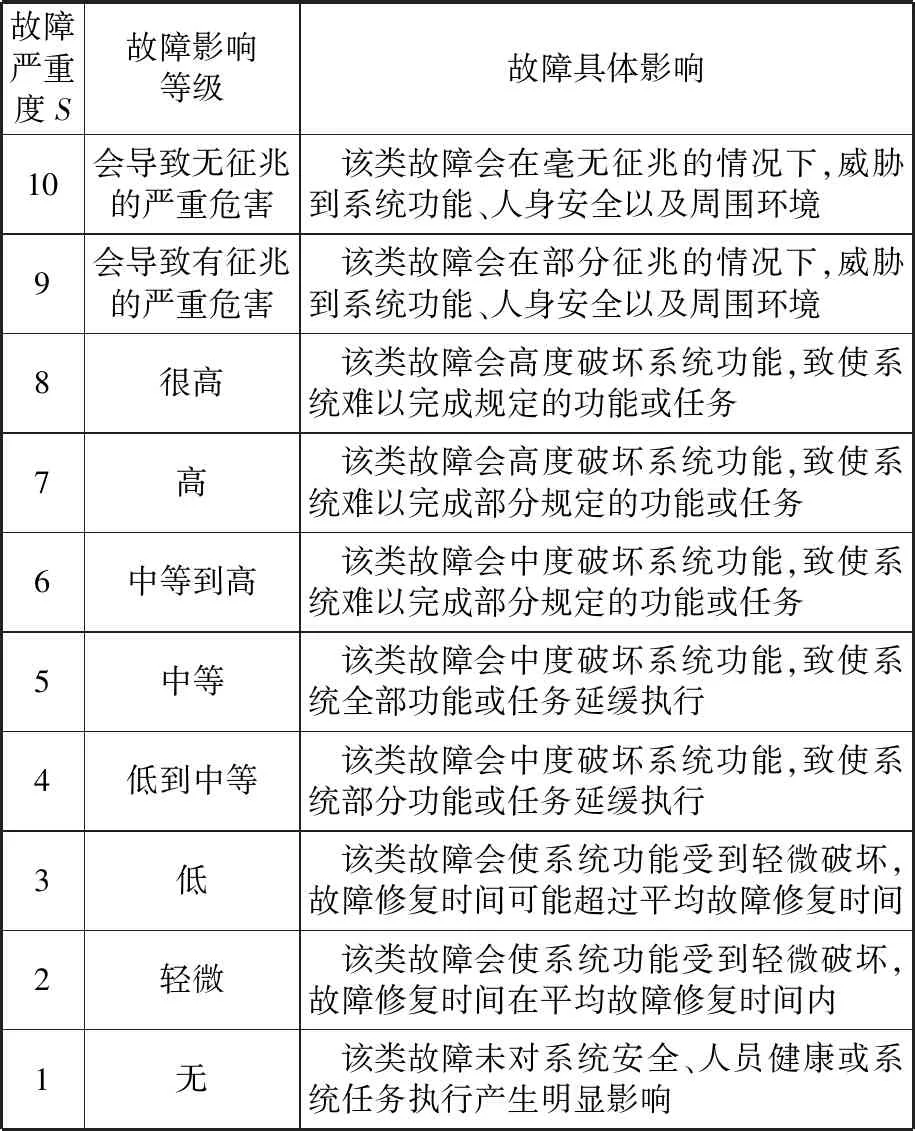
表1 故障嚴重度排序等級

表1中的這類故障嚴重等級雖然能夠為系統分析人員提供一些有價值的故障嚴重性信息，但其測度結果帶有一定的主觀色彩，且有時難以反映系統及其組成單元的真實情況。首先這些等級是在故障影響等級與故障嚴重度線性相關的假設下制定的；其次這些等級之間的乘除運算是缺乏意義的，如不能簡單地認為導致無征兆嚴重危害的故障嚴重度是導致中等危害的故障模式嚴重度的兩倍。因為相對于輕微故障，嚴重故障對系統、人員以及周圍環境造成的破壞性更大，故人們為了消除這種故障所帶來的不良后果所需的資源更多，即故障影響等級越高，相鄰影響等級故障之間的嚴重度差別越大，但如圖1所示，在兩者線性相關的假設下，ΔS45=ΔS78，這顯然是不符合工程系統實際的。

圖1 線性假設下故障影響等級與嚴重度之間的變化關系示意圖Fig.1 Relationship between the impact ranking andfault severity under the linear hypothesis

圖2 故障嚴重度等級非線性轉換示意圖Fig.2 Nonlinear transformation of fault severity ranking

(1)

式中，ξ為故障嚴重度集中水平；a0、c0、c1均為待定參數；n為單元個數。

根據文獻[9-10]中關于兩種非線性轉換函數的參數賦值與求解方法，求得不同非線性轉換方法下的故障嚴重等級變換值，如表2所示。

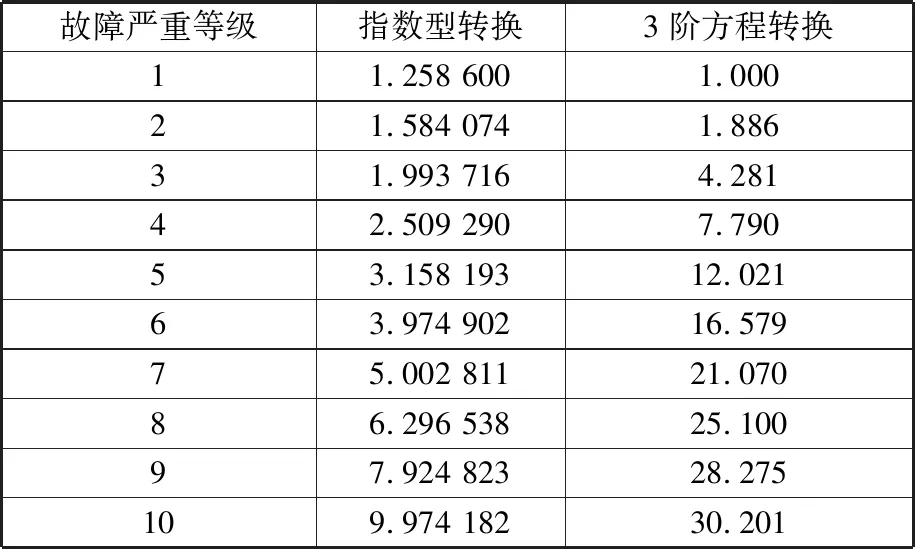
表2 不同方法求得的故障嚴重等級非線性變換值

根據故障嚴重等級非線性轉換原則，故障影響等級越高，相鄰影響等級故障嚴重度之間的差別越大。為了評判各個方法對故障嚴重等級的轉換效果，求得經由不同非線性函數轉換得到的故障嚴重度在各個影響等級的相對變化率(圖3)：

圖3 不同非線性函數對故障嚴重等級的轉換效果Fig.3 Different nonlinear transformations offault severity ranking

為了使故障嚴重等級非線性變換函數更貼近單元不同影響等級故障所導致的后果差異性，本文針對以上兩種非線性轉換函數的不足，提出了一種二次型變換函數，旨在保證轉換后故障嚴重度函數單調增長的同時反映故障本身的特性變化。構建步驟如下:

1.2 共因故障聯合嚴重性測度

當共因故障發生時人們不僅要逐個修復每個單元的單一故障，還需要額外增加資源以消除由于故障之間的關聯性所帶來的額外危害性，因此可將共因故障的聯合嚴重度定義如下。

定義1 對于任一共因部件組C，其所有單元同時發生故障時所造成影響的嚴重程度為

(2)

值得注意的是，隨著同時發生故障的單元數量增加，km值也將逐漸增大，這是因為共因部件組所包含的單元數量越多，故障之間的關聯性越大，由此而造成的故障消除資源投入量越多。

2 考慮共因故障影響的單元故障嚴重性Shapley值測度模型

系統中不同的組成單元有可能從屬于不同的共因部件組，而且同一組成單元也有可能從屬于多個不同的共因部件組。為了合理測度共因故障影響下的系統組成單元故障嚴重性，需要確定單元在不同共因部件組所發揮的作用大小，即該單元故障對不同共因故障聯合嚴重度的期望貢獻度。

根據合作博弈思想，若有n個參與主體，則集合N={1,2，…，n}的任一子集C(C?N)稱為合作博弈的一個聯盟，包括空集聯盟以及所有參與人的總聯盟。聯盟特征函數v(C)表示聯盟內參與主體共同協作時獲得的總效用。通常在合作博弈中隱含有以下兩個假設：①參與主體清楚地知道組成每個聯盟所能產生的總效用值；②參與主體需要完全參與到一個特定聯盟中。

當共因故障誘因被觸發時，系統中至少有兩個組成單元(或子系統)發生故障，此時可以認為同時發生故障的單元在共同故障原因促發下產生了某種程度上的合作關系，因此，本文借用合作博弈思想，將共因故障發生時出現故障的單元看作是合作博弈中的參與主體。聯盟即共因部件組，由在不同原因影響下同時發生故障的單元(或子系統)構成。相應的特征函數v(C)表示共因部件組C內參與單元同時發生的故障對系統、人員以及周圍環境所造成后果的嚴重程度。分配向量則是將共因故障嚴重度分配至共因部件組內單元所得到的向量。

根據合作博弈效用分配原則以及解的性質等，可將合作博弈分配解分為核心、Shapley值、談判集以及內核與核仁等[11]。其中，Shapley值方法[12]不僅計算過程簡便且最終結果具有穩定性(解存在且唯一)、公平性等，因此本節運用Shapley值求解單元故障嚴重性。

根據Shapley值的構建思想，需要首先確定共因部件組的形成概率,然后計算系統組成單元對各個不同共因部件組故障聯合嚴重度的邊際貢獻，最后求解單元對系統故障危害性的期望貢獻度。

本節將單元對共因部件組的參與方法定義為其在不同共因部件組中的排列組合形式。由于各個單元對不同共因部件組的參與情況是隨機的，對于包含n個組成單元的系統，根據單元加入各個共因部件組的先后順序和共因部件組內的單元總體數量可確定共有n!種不同的參與方法。為確定某一包含單元i的共因部件組Ci的形成概率，現將系統全集I拆分成三部分進行考慮：參與單元i、單元i參與之前的共因部件組Ci即{Cii}以及全集的剩余部分{ICi}。

單元i對共因部件組Ci故障嚴重度的邊際貢獻可表示為

ψCi=S′(Ci)-S′(Cii)

(3)

式中，S′(Ci)為共因部件組Ci內單元同時發生故障的聯合嚴重度；S′(Cii)為從共因部件組Ci中去除單元i后的單元同時發生故障的聯合嚴重度;k|Ci|為共因部件組Ci對聯合故障嚴重度的影響系數。

因此，在共因故障影響下，對于任一包含n個單元的系統，某一組成單元i對系統故障危害性的期望貢獻度，即故障修正嚴重度為

(4)

式中,P為共因部件組的形成概率。

3 案例研究

在工程實際中，數控機床各組成單元(或子系統)的故障并不是獨立存在的，存在某些原因導致多個單元(或子系統)同時發生故障的現象[10]。主軸作為數控機床的核心子系統，在數控機床的設計、制造以及運行過程中，都起著至關重要的作用。

某型號數控機床主軸系統的功能結構如圖4所示，該主軸系統的組成單元包括啟動組件、支撐組件、潤滑組件、密封組件、測量組件以及制動組件等。在系統運行過程中，系統分析人員要在共因故障存在的條件下測度各個組成單元的故障嚴重性，以提前發現系統中的各種缺陷和薄弱環節，并盡早采取有效的改進和補償措施。

圖4 某數控機床主軸系統功能結構圖Fig.4 Functional configuration diagram of spindlesystem of a CNC

在系統運行初期，系統分析人員還沒有意識到共因故障的存在，只能根據各個單元的單一故障特征，按照原有工程手冊中的評定原則對系統組成單元的故障嚴重度定級，結果見表3。

表3 單元單一故障嚴重等級

隨著系統的運行，工作人員對系統的認知也逐漸加深，并且意識到了共因故障的存在及其帶來的危害性。為了重新測度系統各個組成單元的故障嚴重性，首先要選擇合適的故障嚴重等級非線性轉換函數。在已有指數型變換函數以及Copula 3階方程的基礎上，重新構建了二次型變換函數并令Ε1=1,Ε2=25，求得ξ=5.83,γ=0.235,b=-4.48。

計算共因故障聯合嚴重度時，將k值設定為k1=0,k2=0.1,k3=0.2,k4=0.3,k5=0.4,k6=0.5。根據式(4)可求得不同非線性變換下考慮共因故障影響的各個單元故障嚴重性Shapley值測度表達式：

(5)

i=1,2,3,4,5,6

代入數據得到最終的故障嚴重性測度值,如表4所示。

表4 共因故障影響下某數控機床主軸系統組成單元故障嚴重性Shapley測度值

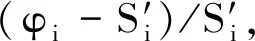
圖5 共因故障對于某數控機床主軸系統組成單元故障嚴重度的影響示意圖Fig.5 The influence of common cause failure on thefault severity of the spindle components in a CNC

由圖5可知，不同轉換方法下的單元故障嚴重度相對變化趨勢大體相似，但3階方程的變化幅度最大，主要原因在于其函數變化率的拋物形波動。對于系統組成單元，不同的轉換方法都顯示密封組件的變化最大，而制動組件的變化最小，這是因為密封組件對共因故障的期望貢獻值較大，即與其他組件相比，密封組件與其他單元的關聯性較強；而制動組件相對獨立，與其他組件的相關性較弱。由此，系統單元故障嚴重性Shapley測度值從側面剖析了共因故障的內部機理，解構了共因部件組內的單元特征。

4 結論

(1)在單一故障嚴重等級非線性轉換的基礎上，提出了共因故障聯合嚴重性測度方法。在對傳統故障嚴重等級進行非線性轉換的基礎上，結合單元故障間的相關性影響，定義了共因故障的聯合嚴重性及其測度方法。

(2)構建了一種考慮共因故障的單元故障嚴重性Shapley值測度模型。基于合作博弈思想，根據Shapley值算法步驟，求解出了系統組成單元對各個共因故障聯合嚴重度的期望貢獻。

(3)通過某型號機床主軸系統的故障嚴重度分析實例，介紹了所提方法在共因故障存在條件下合理測度單元故障嚴重性的應用可行性，為進一步識別系統缺陷與薄弱環節提供了決策支持。