面向響應準確度的參數不確定性模型確認方法
項涌涌 潘柏松 羅路平 謝少軍
浙江工業大學機械工程學院,杭州,310014
0 引言
由于存在物理試驗成本和客觀條件等限制,計算機仿真建模和分析已逐漸應用于設計及評估航空航天、機械等領域的復雜系統。高精度的數值模型是開展有效仿真分析的基礎, 滿足使用要求的數值模型才可用于仿真分析。工程實際中,普遍存在概率與區間混合不確定性情況[1-2],有些模型參數可獲得充足樣本數據來構建精確的概率分布;而有些模型參數試驗成本高及難度大,難 以獲得足夠樣本數據來精確描述,只能估計其變化區間。雖然多數情況下估計區間的不確定性水平僅略大于真實區間的不確定性水平,但概率與區間混合時會導致模型輸出響應的不確定性水平過高,從而使得模型可信度大幅降低。
目前模型確認方法廣泛應用于評價和提高建模可信度,最早由美國能源部應用于戰略武器管理的可靠性評估和決策[3-4]。由于工程領域對仿真分析可信度要求的提高,模型確認方法正大量應用于計算力學、汽車等工程領域[5-6]。隨著模型確認技術的應用推廣,人們逐漸認識到僅僅實施評估模型精確度的模型確認過程并不能滿足工程實際需求,需對未達到要求的模型進行模型修正[7]。
模型確認方法可分為基于貝葉斯理論的貝葉斯方法[8]和基于統計及推斷方法的非貝葉斯方法[9-10]兩大類。KENNEDY等[8]提出了基于貝葉斯理論的模型修正方法;LIU等[11]針對熱傳導問題的模型修正,采用貝葉斯方法來提高模型精度;HASSELMAN等[12]針對汽車碰撞模型提出了一種基于模型響應值均方差結果的修正方法。
近年來,為確保仿真工作具有實際應用價值和意義,對模型確認問題的研究已受到國內學者們的重視。張保強等[13]將貝葉斯方法用于圣地亞熱傳導問題的模型修正中,并建立相應的貝葉斯框架;何成等[14]分析了基于徑向基模型的不確定性結構動力學模型非概率型區間修正方法;肖釗等[15]針對試驗數據較少的情況,利用區間方法量化不確定性,并提出了對應模型確認方法;方圣恩等[16]提出了針對結構參數不確定性的隨機模型優化方法;姜東等[17]基于區間分析提出了不確定性結構動力學模型修正方法。綜上可知,人們已開展了一些模型確認問題的工作,并取得了一定成果,但針對概率與區間混合不確定性情況的研究并不多,且總體上就模型確認問題并未達成統一共識。
由于存在不確定性傳播的問題,在概率與區間混合不確定性情況下,模型輸出響應的數值結果為非精確概率。本文通過數值結果非精確概率累積分布函數(cumulative distribution function,CDF)與試驗結果經驗累積分布函數(empirical cumulative distribution function,ECDF)之間的面積極大值求解模型確認準則參數,并對模型確認結果進行評估,對于不滿足確認評估標準的模型,以區間變量表征的不確定性參數為對象實施修正,最后將模型確認方法應用于圣地亞熱傳導問題的算例中,并驗證了所提方法的有效性。
1 參數不確定性模型確認過程
實際工程模型中普遍存在隨機不確定性參數、認知不確定性參數、確定性參數混合情況,本文針對區間變量表征認知不確定性參數,概率變量表征隨機不確定性參數及確定性參數的混合情況進行了研究分析,得到模型函數可表示為
Y=g(X,Z,M)
(1)
式中,X為區間變量矢量;Z為概率變量矢量;M為確定性變量矢量;Y為模型輸出響應(隨機變量)。
受不確定性混合影響,模型中只要存在參數不確定性水平略大于真實水平的情況,就會使模型輸出響應的不確定性水平過高,從而需進行模型確認以保證響應準確度和建模可信度。
模型確認的目的是量化數值模型與真實物理系統的差異程度,并基于差異程度確定模型預測精度。在模型確認過程中,對于未達到模型確認要求的數值模型,需通過模型修正以減小模型誤差,從而使數值模型滿足預期要求。在參數不確定性模型中對模型參數進行修正,概率與區間混合不確定性情況的修正參數為區間變量表征的不確定性參數。
真實物理系統的量化表征是以輸出響應的試驗數據為基礎,響應試驗誤差會直接影響確認結果的可信度,因此本文將響應試驗誤差視為數值模型的隨機不確定性參數來開展模型確認過程。模型確認實施步驟包括模型確認試驗,不確定量化,應用確認準則進行模型確認評估,對不滿足要求的模型進行參數修正,以及模型應用等,見圖1。

圖1 參數不確定性模型確認過程Fig.1 Validation process of parameteruncertainty model
模型確認試驗和確認準則在模型確認過程中至關重要,模型確認試驗的設計、執行、分析是以定量確定數值模型及其載體(仿真軟件)在多大程度上能夠代表實際系統為目的[6]。不同工程實際問題應根據確認的需求對系統、子系統、部件和單元的各個層面分別進行試驗測試。模型確認準則主要可分為圖像對比準則、頻率準則、經典假設檢驗法、貝葉斯因子、面積度量準則等[18]。在模型確認過程中,需根據實際問題應用合理的確認準則以獲得可信的確認結果。
2 概率與區間混合不確定性下參數不確定性模型確認理論
2.1 區間變量
區間變量的數學定義為[19]
XI=[XL,XU]=[x|XL≤x≤XU,x∈R]
(2)
式中,x為實數集變量;XL、XU分別為區間下限和區間上限。
區間變量也可利用區間中點和區間半徑來表示,即
XI=[XC-XR,XC+XR]
(3)
式中,XC為區間中點;XR為區間半徑。
應用區間變量來量化不確定性,區間可靠度是評價量化結果的指標之一,區間可靠度H可用區間置信系數來定義[20],即
H=PXI{XL≤x≤XU}∝XR
(4)
其中,PXI為區間變量XI包含參數所有值的概率。H與區間半徑XR成正比(即區間半徑XR越大,區間變量的置信水平越高,區間估計越可靠)。
2.2 模型輸出響應數值結果
不確定性傳播中概率與區間混合不確定性情況下模型的輸出響應數值結果為非精確概率,本文采用概率盒(probability box , P-box)來表征[21]。如圖2所示,概率盒將上下兩條累積分布函數(CDF)作為邊界,數學定義為[22]
(5)


圖2 概率盒示意圖Fig.2 Schematic diagram of probability box
2.3 模型確認與評估
面積度量準則[23]是一種有效的模型定量確認準則,以仿真值CDF與試驗值ECDF的面積差值作為準則值。為確保概率與區間混合不確定性情況下模型確認的有效性,本文考慮確認準則值的量綱一性,以面積度量準則為基礎,根據數值結果概率盒上下邊界與試驗結果ECDF之間的面積極大值定義了模型確認準則,具體表達式如下:
(6)
式中,VP為模型確認準則參數;max{·}為求解最大集合元素函數;B為輸出響應試驗數據的中點;Se(y)為響應試驗結果ECDF。
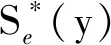

圖3 概率盒邊界與試驗結果ECDF的面積差值圖Fig.3 Different area between probability boxboundary and the ECDF of test results
模型確認準則可量化試驗結果與仿真結果的差異,求解得到的VP值越大,表明數值模型和真實物理對象的吻合程度越低,為此提出模型確認評估標準,即
VP≤δ
(7)
其中,δ為確認標準值,根據模型實際應用條件取某一常數值。當數值模型有較高要求時,需設定較小的δ值,反之則可設定較大的δ值。
2.4 模型修正
當確認準則值大于標準值δ時,需對模型參數進行修正。模型參數修正實質為優化待修正參數,本文以模型確認評估標準和模型參數初始值 為約束條件,以待修正區間不確定性參數總置信水平最大為目標實施參數修正,得到優化模型如下:
(8)
式中,H(X)為待修正區間不確定性參數總置信水平函數;Θ為模型參數初始值域。
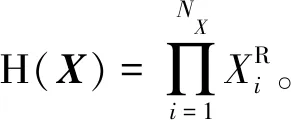
3 算例(圣地亞熱傳導問題)
圖4為一維瞬態圣地亞熱傳導模型示意圖[25],數學模型可表示為
(9)
x=(q,L,t,γ)β=(k,cV)
式中,θi為初始溫度,這里為25 ℃;q為熱流密度;L為板厚;k為材料熱導率;cV為體積熱容;γ為表面距離;t為時間;x為受控輸入參數矢量;β為待修正參數矢量。

圖4 熱傳導模型示意圖Fig.4 Schematic diagram of thermal challengeproblem model
圣地亞熱傳導模型的預測目標為受控輸入參數矢量x=(3 500 W/m2,0.019 m,1 000 s,0 m)時,溫度大于900 ℃的概率小于0.01,即
P{θ(x,β)>900 ℃}<0.01
(10)
圣地亞熱傳導問題中試驗誤差無法避免,本文通過考慮模型輸出響應溫度的試驗誤差來開展模型確認,則熱傳導問題數值模型可表示為
θ(x,β,εe)=θ(x,β)+εe
(11)
其中,受控輸入參數x為確定性變量矢量;待修正參數β為認知不確定性變量矢量,應用區間變量表征;響應試驗誤差εe為隨機不確定性變量,應用概率分布表征。
模型確認熱傳導問題試驗分為材料特性(material characterization,MC)試驗,整體確認(ensemble validation,EN)試驗,認證(accreditation validation,AC)試驗,所有試驗根據數據量的大小分為低水平、中水平和高水平等級。由于高水平試驗數據量與其他兩個水平的數據量差距較小,為確保模型確認的有效性,故本文選用高水平試驗數據進行熱傳導問題模型確認,試驗數據詳見文獻[25]。
溫度對待修正參數有較大影響,本文考慮待修正參數的溫度依賴性求解函數方程,分析試驗數據可知,體積熱容cV為獨立變量,則體積熱容區間變量的表達式如下:
(12)
式中,N為試驗數據數量。
材料熱導率k對溫度存在依賴性,建立關于溫度θ的一維線性回歸模型,表達式如下:
k=a+bθ+ω
(13)
根據MC試驗數據求得參數a為0.051 2,b為2.25×10-5,誤差項ω~N(0,0.005 32),根據正態分布求解誤差項區間變量形式(即ωI=[μ-3σ,μ+3σ]),得到含區間變量的方程如下:
k=0.051 2+2.25×10-5θ+[μ-3σ,μ+3σ]
(14)
式中,μ為正態分布均值;σ為正態分布標準差。
根據文獻[7]可得試驗誤差εe的分布為εe~N(0,5.252)。
熱傳導問題模型確認中可用函數表示式來表示預測溫度與各參數之間的關系:θ=g(x,β,εe),將區間變量(式(12)、式(14))及各概率分布代入上述函數表達式,可得熱傳導問題模型確認方程如下:
(15)
熱傳導問題模型確認方程是以θ為變量的非線性方程,可進行優化求解。本算例的模型確認標準值設定為δ=0.3,應用所提確認準則進行模型確認,熱傳導問題模型確認評估的表達式為
(16)

圣地亞熱傳導問題設計進行了不同的EN試驗和AC試驗,EN試驗的高水平數據為在0~1 000 s范圍內,以間隔100 s選取得到10個時間點的4組試驗數據,每組試驗重復4次;AC試驗高水平數據為在0~1 000 s范圍內,以間隔50 s選取得到20個時間點的3組試驗數據,每組試驗重復2次。表1和表2分別列出了熱傳導問題各EN試驗參數和AC試驗參數。

表1 整體確認試驗參數

表2 認證試驗參數
本文綜合應用EN試驗和AC試驗的高水平數據進行模型確認,根據表1和表2中的具體參數值,將不確定性參數表征值代入式(15),運用雙層采樣法得到θ的概率盒模型,最后根據式(16)分別求得各時刻下的VP(t)。
圖5a為EN試驗條件下未修正確認準則的參數曲線圖,可以看出,所有試驗序號各時刻下的確認準則參數值均小于0.3,滿足確認評估要求。圖5b為AC試驗條件下未修正確認準則的參數曲線圖,可以看出,在0~1 000 s范圍內AC1試驗的確認準則參數值滿足要求;而AC2試驗的確認準則參數值有部分不滿足要求,且t=200 s為確認準則參數曲線極值點(即VP(t=200 s)為0.36>δ);AC3試驗中t=450 s為曲線極值點(即VP(t=450 s)為0.7>δ),且大部分AC3試驗確認準則的參數值不滿足要求。
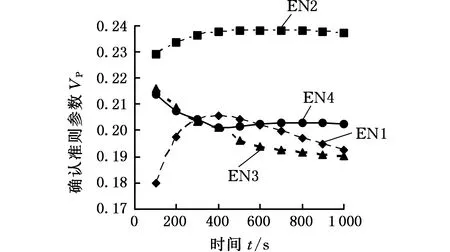
(a)整體確認試驗
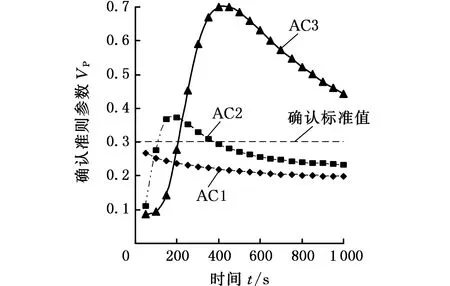
(b)認證試驗圖5 未修正模型確認準則參數值Fig.5 Values of uncorrected model validationcriteria parameters
在熱傳導問題中,AC2試驗和AC3試驗的確認準則參數值不滿足確認評估要求,應進行模型參數修正。由于AC3試驗條件下確認準則參數值不滿足要求的比例遠大于AC2試驗條件下的比例,且AC3試驗條件下準則參數值曲線的極值點VP(t=450 s)=0.7大于AC2試驗條件下準則參數值曲線極值點VP(t=200 s)=0.36,故依據AC3試驗進行模型參數修正。AC3試驗的準則參數值曲線為開口向下的拋物線,在t=450 s時達到最高點,所以修正后滿足VP(t=450 s)≤δ的條件,就可使所有曲線均滿足要求。基于AC3試驗條件下t=450 s的確認結果修正模型參數,得到優化模型如下:
(17)
目標函數經簡化后,運用遺傳算法求解優化模型,表3為模型參數修正結果,表4為修正前后參數值對比。
基于修正后參數值進行模型確認,圖6a和圖6b分別為修正后EN試驗和AC試驗條件下的模型確認準則參數值曲線。由圖6可知,修正后全部確認試驗所有時刻點的模型確認準則參數值均小于0.3,數值模型滿足使用要求。

表3 模型參數修正結果
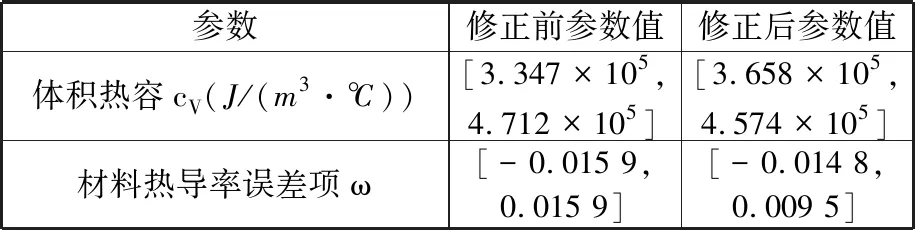
表4 參數修正前后結果對比

(a)整體確認試驗

(b)認證試驗圖6 已修正模型確認準則參數值Fig.6 Values of model validation criteria parametersafter correction
將修正后的模型參數代入式(10)求解,采用蒙特卡羅法抽樣(抽樣次數為1×106次)可得到失效概率。圖7為修正后溫度θ的累積分布函數曲線,預測結果見表5。由表5可知,模型未修正時,溫度超過900 ℃的概率為0.078 1,模型修正后,溫度超過900 ℃的概率為0.016 2,預測精度得到明顯提高。
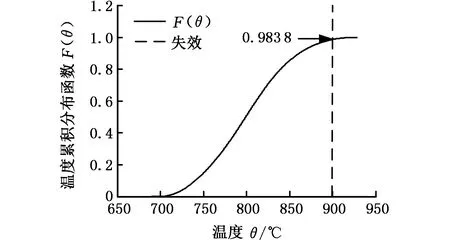
圖7 修正后溫度的累積分布曲線Fig.7 The CDF curve of temperature after correction

模型預測未修正修正后P{θ(x,β)>900 ℃}0.078 10.016 2
熱傳導問題中失效概率的目標要求不能大于0.01,采用本文方法得到的模型預測概率結果也不滿足要求,這與同類文獻[11,26-28]的結論一致。采用不同方法的模型修正對比見表6,其中文獻[11,27]基于貝葉斯原理實施模型修正。
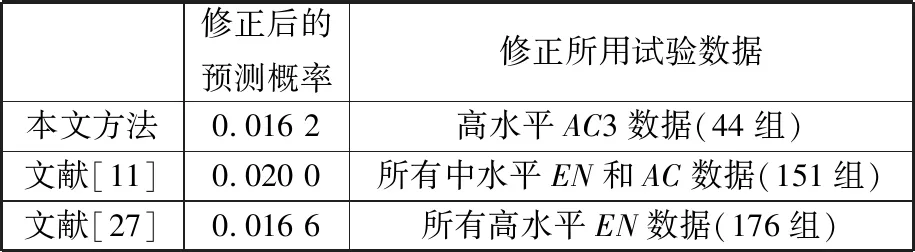
表6 不同方法模型修正對比
由表6可知,三種方法的修正后模型預測概率十分相近,但文獻[11,27]所用試驗數據量是本文方法所用試驗數據量的3倍以上。基于貝葉斯的模型修正方法以增加試驗數據量為基礎,且模型參數先驗分布的確定存在較大主觀性,因此,在工程實際試驗難度較大、試驗成本較高的情況下,本文方法具有明顯的優勢。
4 結論
(1)在概率與區間混合不確定性情況下,本文的模型確認準則依據數值結果概率盒邊界與試驗結果經驗累積分布函數之間的面積極大值進行定義,可獲得有效可信的模型確認結果值,為后續確認評估及修正奠定了基礎。
(2)以待修正區間不確定性參數總置信水平最大為修正目標,以模型確認評估標準和模型參數初始值為約束條件,目標函數簡化后應用遺傳算法修正模型參數,獲得的修正結果具有可信性。
(3)將本文方法應用于圣地亞熱傳導問題,經模型確認后熱傳導模型的預測精度有明顯提高,模型可信度和響應準確度有較大提升,獲得了與同類文獻相同的預測結果。修正后模型預測概率與基于貝葉斯的模型修正方法得到的修正后預測概率的結果十分相近,但本文方法所用試驗數據量有明顯減小。在試驗難度較大、試驗成本較高的情況下,本文方法比基于貝葉斯的模型修正方法更具優勢,具有較好的應用前景。

