定子水冷永磁同步電機多工況熱特性的研究

劉 威，劉慧娟，杜晉文，宋騰飛

(北京交通大學，北京100044)

0 引 言

永磁同步電機因運行效率高、功率密度大等優(yōu)勢，近年來得到電動汽車企業(yè)的廣泛青睞。而永磁同步電機的高功率密度會導致更高的熱流密度，同時考慮到電機在電動汽車中安裝空間等的限制會影響到電機的散熱，因此，在永磁同步電機的開發(fā)設計階段，必須研究和分析預測電動汽車用永磁同步電機的溫升情況，提高其運行的可靠性與高效性。

國內(nèi)外學者對電機溫度場的研究主要包括兩種方法，一種是經(jīng)典的熱網(wǎng)絡方法[1-2]及其改進的實用型簡化熱網(wǎng)絡方法[3-4]，一種是有限元法。熱網(wǎng)絡法由于電機參數(shù)易于修改以及計算速度快等優(yōu)點，在工程實際中應用廣泛，但對于一些極端的運行工況，往往不能得到可靠的溫升預測結果；有限元法，隨著計算機技術和數(shù)值計算方法的廣泛應用，計算精度較之于熱網(wǎng)絡法更準確，應用范圍也更廣泛。針對兩種方法的各自優(yōu)點，文獻[5]建立了電機的熱網(wǎng)絡模型并與實驗進行了對比，驗證了熱網(wǎng)絡法的有效性與快速性。文獻[6-7]在熱網(wǎng)絡法的基礎上提出了修正的熱網(wǎng)絡計算方法，瞬態(tài)和穩(wěn)態(tài)下溫度場更加接近實驗值。隨著計算機技術的發(fā)展，有限元法得到了廣泛應用，文獻[8]將三維有限元計算的熱阻參數(shù)應用于熱網(wǎng)絡法中進行耦合求解，指出三維有限元法的準確性。考慮到熱網(wǎng)絡法的快速性以及有限元法的準確性，文獻[9-10]等分別對轉子、定子以及氣隙等綜合使用了熱網(wǎng)絡法和三維有限元法，達到了結果既準確又快速的目的。

本文以一臺采用強迫水冷的80 kW永磁電機為計算對象，利用熱網(wǎng)絡法與有限元法對其進行冷卻系統(tǒng)設計。首先，利用ANSYS Maxwell計算80 kW永磁同步電機各部分對應的損耗；然后，基于Motor-CAD平臺，建立電機的熱網(wǎng)絡模型，并利用Fluent軟件，建立電機的溫度場有限元仿真模型，計算并比較分析該電機在額定轉速工況、峰值轉矩工況和峰值轉速工況下的溫度場分布，確定出不同工況下相對準確而快捷的計算方法，為實際工程中電機冷卻系統(tǒng)的設計和應用提供指導。

1 電機模型以及各部分損耗

電機的實體模型如圖1(a)所示，依照實體模型建立1∶1的仿真模型，如圖1(b)所示。 電機基本參數(shù)如表1所示。

(a) 實體模型

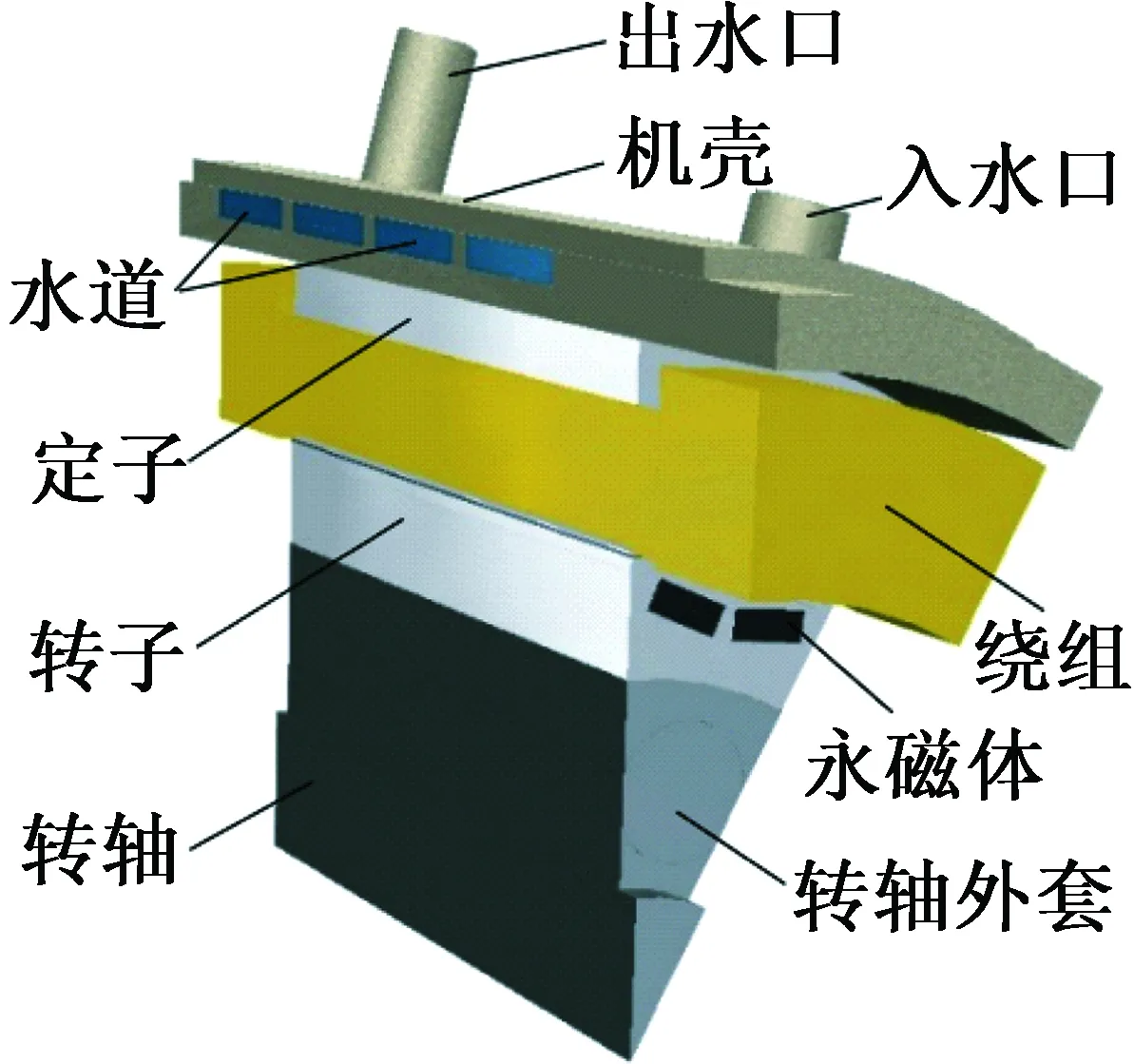
(b) 仿真模型

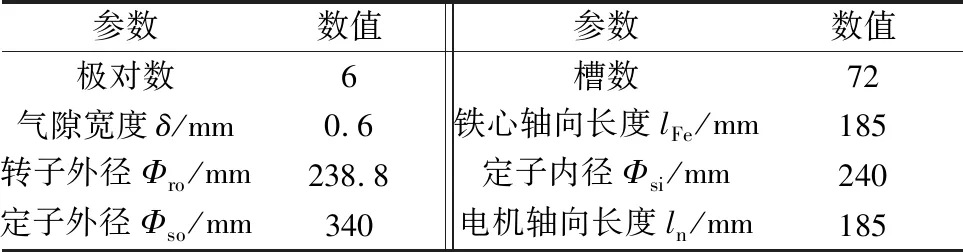
參數(shù)數(shù)值參數(shù)數(shù)值極對數(shù)6槽數(shù)72氣隙寬度δ/mm0.6鐵心軸向長度lFe/mm185轉子外徑Φro/mm238.8定子內(nèi)徑Φsi/mm240定子外徑Φso/mm340電機軸向長度ln/mm185

由于電機定、轉子鐵心齒部與軛部的鐵耗分布不均勻，為了更加準確地計算電機的溫度場分布，以便對電機鐵心齒部與軛部分別加載熱源，故將電機的定、轉子鐵心的齒部與軛部損耗分開計算，同時考慮到剖分的質(zhì)量等因素，確定定、轉子齒部與軛部的分塊如圖2所示。分別在額定轉速、峰值轉矩、峰值轉速三種工況下求得電機各個部分對應的損耗，如表2所示。

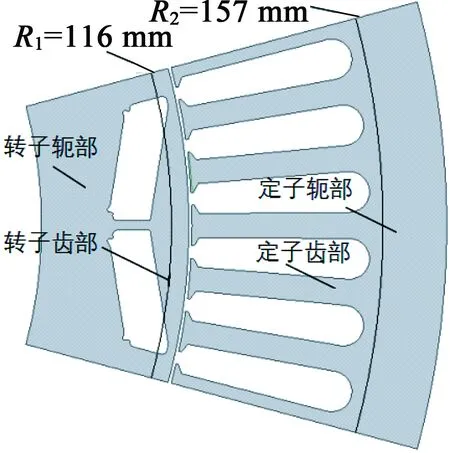
圖2 定、轉子齒部與軛部

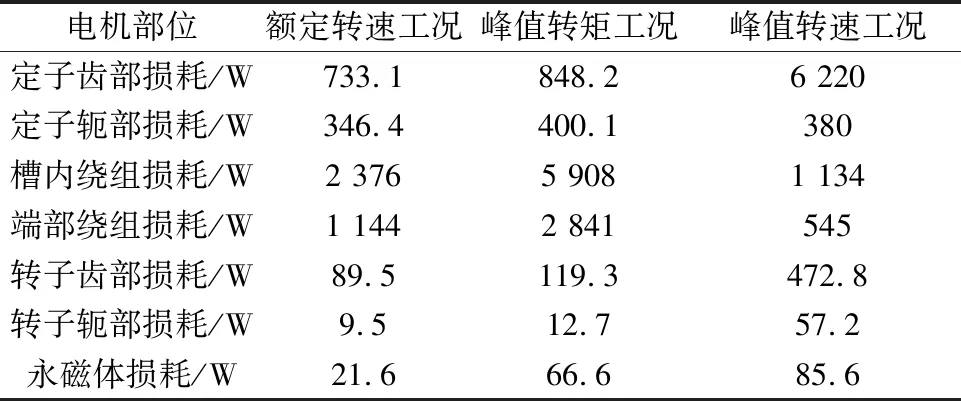
電機部位額定轉速工況峰值轉矩工況峰值轉速工況定子齒部損耗/W733.1848.26 220定子軛部損耗/W346.4400.1380槽內(nèi)繞組損耗/W2 3765 9081 134端部繞組損耗/W1 1442 841545轉子齒部損耗/W89.5119.3472.8轉子軛部損耗/W9.512.757.2永磁體損耗/W21.666.685.6

2 氣隙等效導熱系數(shù)的確定

氣隙由導熱系數(shù)較低的空氣組成，它作為電機機電能量轉換的主要區(qū)域，也是定子與轉子之間熱量傳遞的媒介，考慮到氣隙寬度相較于定、轉子尺寸的數(shù)量級，在電機溫升計算中，氣隙中熱量的傳遞需要引起充分的重視。此外，由于氣隙中的空氣隨著轉子的轉動會做周向的流動以及實際工程中電機定子表面存在的凹槽[11]會增加表面粗糙程度等因素，所以關于氣隙的傳熱處理一直以來是電機溫升計算的難點所在。

考慮到仿真過程中計算資源條件的限制，同時盡可能準確地模擬實際中定、轉子之間的熱對流傳熱情況，綜合考量，在滿足能量守恒定律的前提下，考慮轉子運動對氣隙中空氣流動的影響，得到等效的導熱系數(shù)[11]。氣隙部分的雷諾數(shù)Re采用下式計算[12]：

(1)

式中：D2為電機轉子的外直徑；g為氣隙寬度；nz為轉子轉速；γ為氣隙中空氣的運動粘度系數(shù)。

氣隙的臨界雷諾數(shù)[11]：

(2)

式中：D1為定子鐵心的內(nèi)直徑。

樣機的臨界雷諾數(shù)為824，在不同的工況下，根據(jù)實際雷諾數(shù)與臨界雷諾數(shù)的相對大小，大于臨界雷諾數(shù)的情況，采用如下的導熱系數(shù)計算：

(3)

計算得到各種工況下對應的氣隙等效導熱系數(shù)(忽略空氣物性隨溫度的變化)，如表3所示。

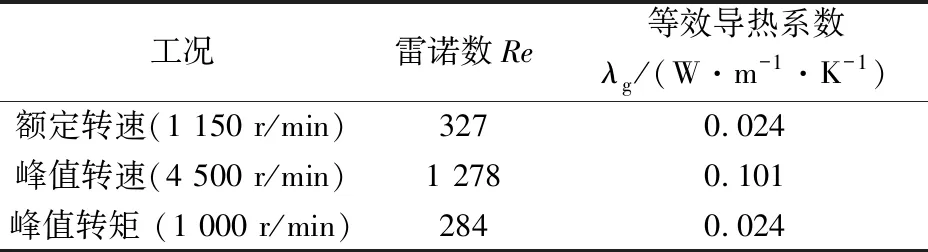
表3 不同工況下氣隙等效導熱系數(shù)

電機機殼外表面等其它部分與空氣接觸的等效散熱系數(shù)如表4所示。

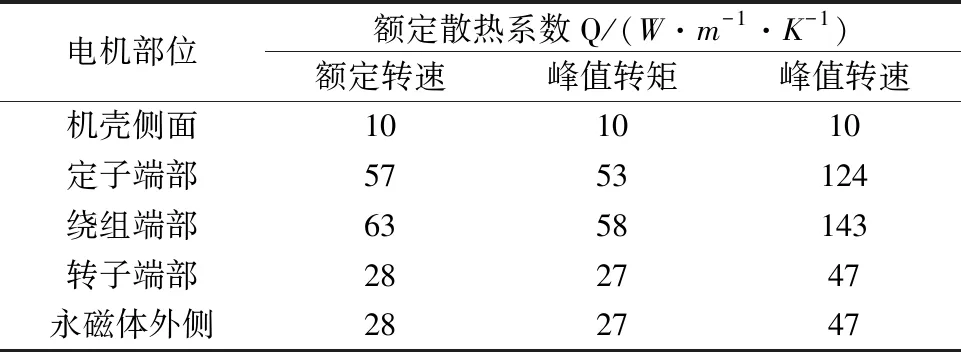
表4 不同工況下電機表面的等效散熱系數(shù)

3 無強制冷卻時電機溫度場分布

為了確定冷卻系統(tǒng)對于電機溫度場分布的影響，本文利用有限元法仿真計算了電機在無強制冷卻時的溫度場分布，仿真結果如圖3所示。從圖3中可以看出，定子槽內(nèi)繞組中部的溫度最高，達到了270 ℃，定子鐵心的溫度達到了250 ℃以上，轉子以及永磁體的溫度遠遠高于200 ℃，當電機的溫度場分布達到穩(wěn)態(tài)時，定子、轉子和繞組的溫度會更高。根據(jù)文獻[13]，對于永磁同步電機，釹鐵硼的工作溫度一般不能超過200 ℃，否則永磁體會出現(xiàn)不可逆退磁，定、轉子鐵心溫度過高會破壞絕緣層、增加鐵耗以及損害其機械強度，一般來說定、轉子鐵心的最高溫度不應超過250 ℃，轉軸的最高工作溫度為200 ℃，所以對于本文研究的永磁同步電機，如果不采用強制冷卻，電機將無法正常工作，樣機必須進一步優(yōu)化。

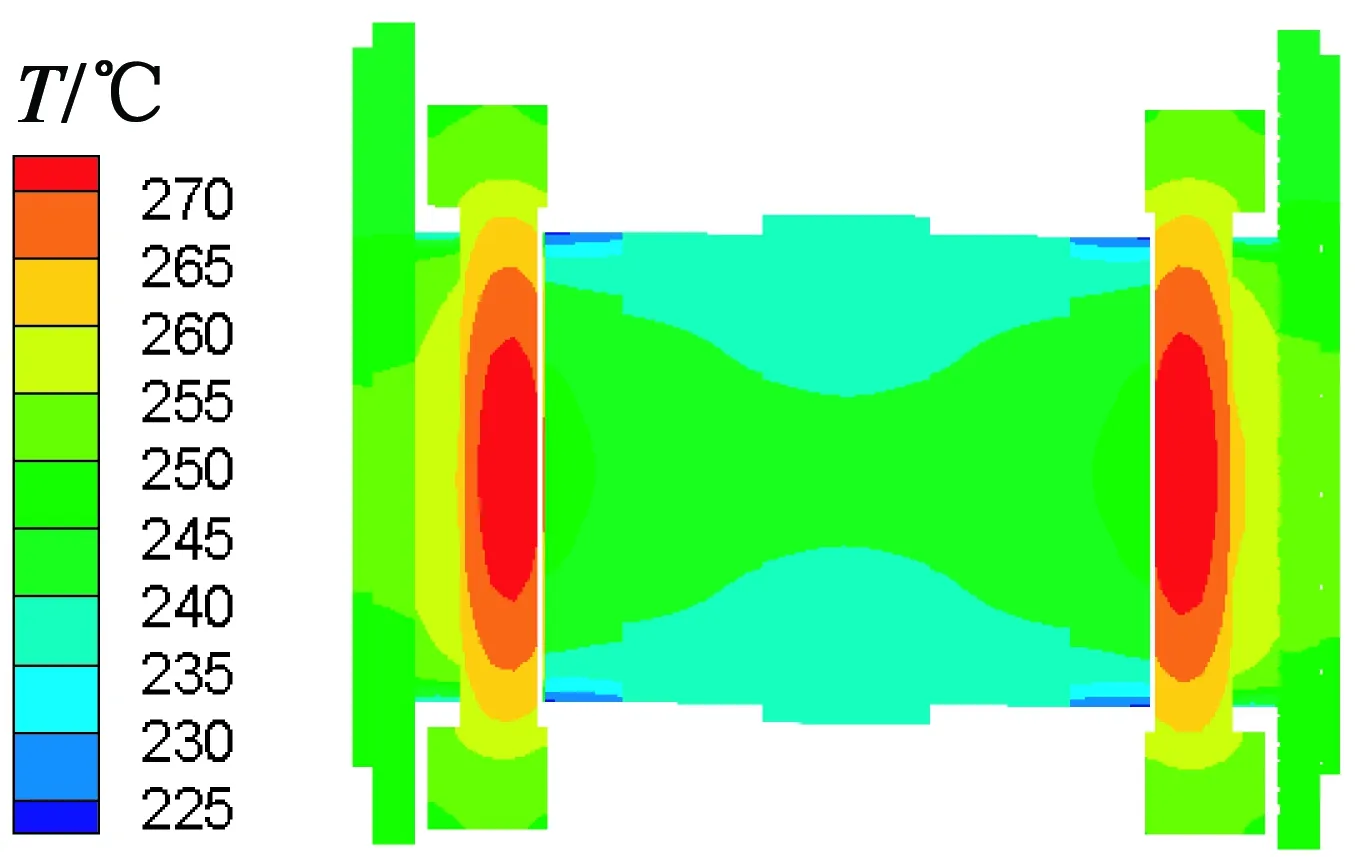
圖3 不使用冷卻液電機溫度場分布

4 熱網(wǎng)絡及有限元法計算永磁電機溫度場

4.1 溫度場實驗測試

電機的溫升試驗中，使用50%的乙二醇水溶液作為冷卻液，注水流速為20 L/min，額定轉速以及峰值轉速工況下冷卻液的初始溫度均為65 ℃，峰值轉矩工況下冷卻液的初始溫度為60 ℃。

實驗過程中，在定子齒部和軛部各埋設2個熱電偶，在定子槽內(nèi)U，V，W三相繞組的中部各埋設1個熱電偶，繞組端部埋設一個熱電偶，測定機殼外表面的溫度，各點溫度數(shù)據(jù)的采樣間隔為1 s，額定轉速以及峰值轉矩工況下測試時間持續(xù)2 h，峰值轉速工況下持續(xù)2 min，定子測試點的位置如圖4所示，測試現(xiàn)場如圖5所示。

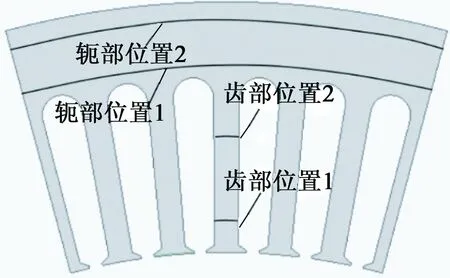
圖4 定子的測試位置

(a) 提供冷卻液的恒溫水箱

在以下各種運行工況溫度場的仿真計算中，所有仿真條件均與實驗條件完全一致，且仿真的溫度采集點也與實驗的溫度采集點完全一樣。

4.2 額定工況穩(wěn)態(tài)溫度場分布

基于Motor-CAD軟件平臺，根據(jù)電機的尺寸建立熱網(wǎng)絡模型，計算額定轉速工況下的軸向溫度場分布，如圖6(a)所示，利用UG(Unigraphics NX)建立電機的有限元仿真模型，并利用Fluent進行溫度場、流體場分析，電機的軸向溫度場分布如圖6(b)所示。

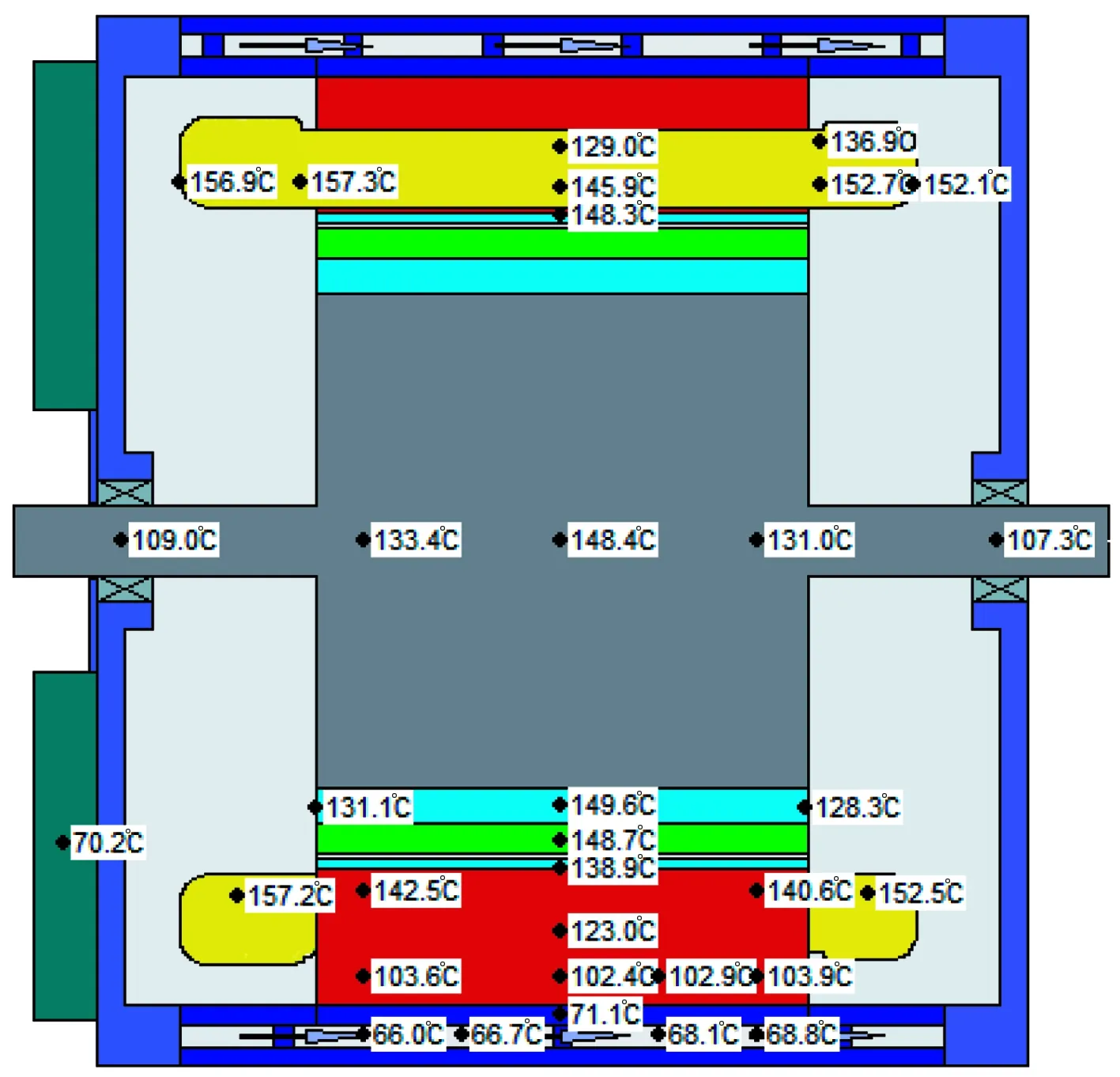
(a) 熱網(wǎng)絡法軸向溫度分布

(b) 有限元法軸向溫度分布

從圖6中可以看出，電機繞組的端部溫度最高，機殼的溫度較低。定子內(nèi)部的繞組由于距離水道比較近，所產(chǎn)生的熱量主要以熱傳導的方式傳遞給電機的定子部分，再通過定子與冷卻液之間的熱對流實現(xiàn)散熱。而端部的繞組與大氣空氣發(fā)生自然對流換熱，散熱相對比較困難，所以溫度最高；同理，定子齒部與軛部接近水道一側的溫度低于遠離水道一側的溫度，冷卻液的溫升較小，大概為3～4 ℃。 熱網(wǎng)絡法計算的轉子齒部中間位置的溫度較高，為149 ℃，永磁體的溫度與轉子很接近；有限元法計算的轉子的溫度分布很均勻，永磁體與轉子的溫度分布相似，約為120 ℃。由于轉子表面與空氣相接觸，散熱很困難，導致轉子的溫度較高。溫度取實驗值中U，V，W三相繞組溫度的平均值，將各個點采集的溫度與仿真值對比，如圖7所示。

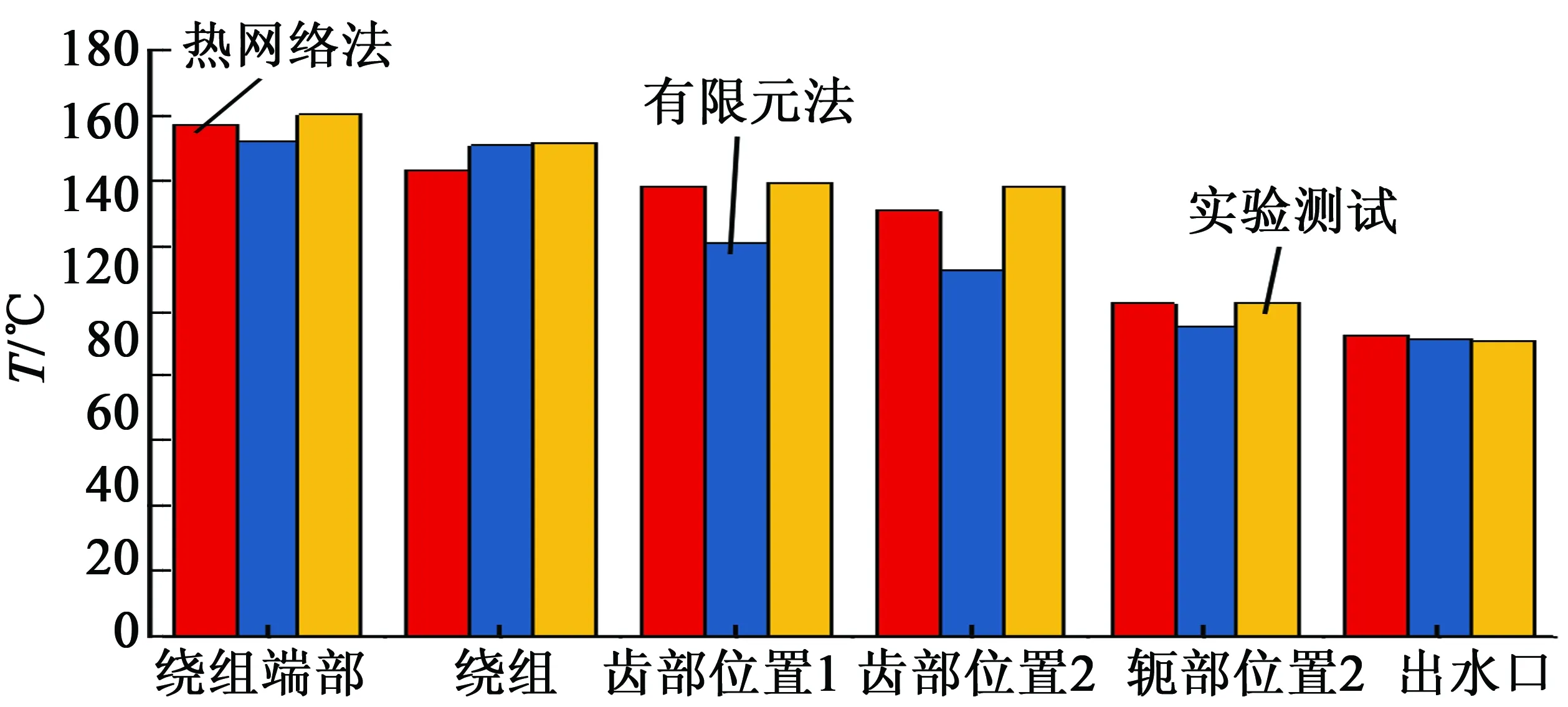
圖7 額定工況仿真與實驗結果數(shù)據(jù)對比

由圖7可以看出，熱網(wǎng)絡法計算結果的誤差均在6%以內(nèi)，結果很可靠，有限元法計算的結果除了定子齒部誤差較大以外，其它部位誤差均在8%以內(nèi)，結果可靠。

4.3 峰值轉矩工況下瞬態(tài)溫度場

峰值轉矩工況下，銅耗的增大導致電機在2 min內(nèi)繞組的溫升非常明顯，其它部位溫升很小，實驗時只測定定子內(nèi)部繞組的溫度。2 min內(nèi)某些時間節(jié)點的瞬態(tài)溫度值如圖8所示。

為了比較兩種方法的計算結果，瞬態(tài)誤差曲線圖如圖9所示。從圖9中可以看出，有限元法計算的繞組溫度誤差均比熱網(wǎng)絡法小，兩種方法的誤差均在10%以內(nèi)，計算結果均可靠。不過，隨著時間的推移，兩種方法的誤差均有增大的趨勢。

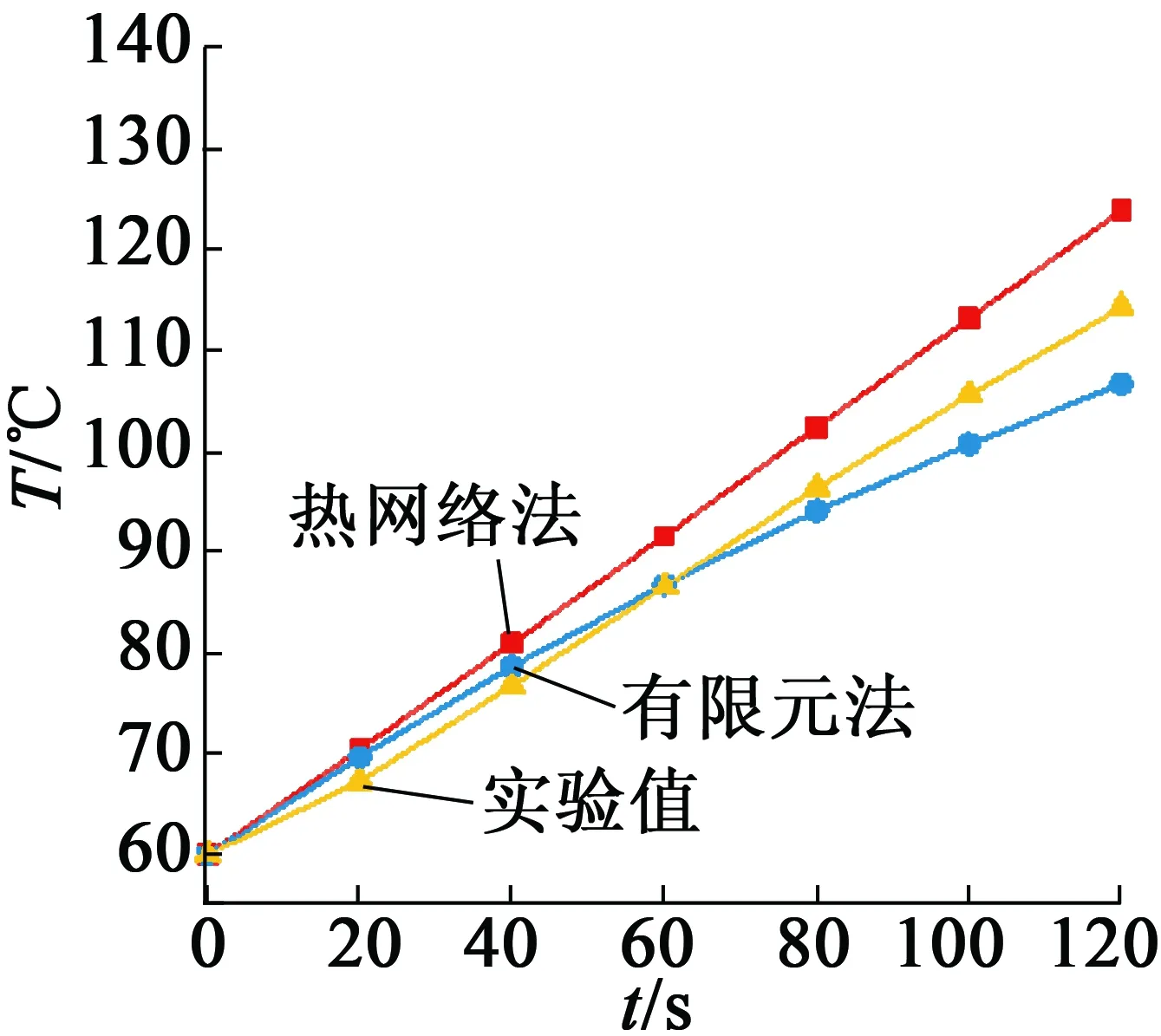
圖8 峰值轉矩工況下兩種方法的瞬態(tài)溫度比較

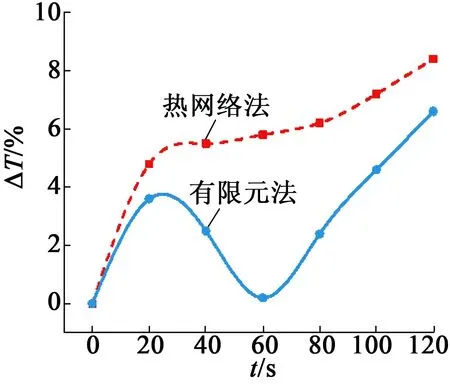
圖9 峰值轉矩工況下兩種方法的瞬態(tài)誤差比較

4.4 峰值轉速工況下穩(wěn)態(tài)溫度場

峰值轉速工況下，轉子的轉速較大，氣隙中空氣運動狀態(tài)變得復雜，熱網(wǎng)絡法的仿真結果與實驗值偏差很大，特別是轉子的溫度遠遠超出了預期值，計算結果不可靠。有限元法利用靜態(tài)下氣隙的等效導熱系數(shù)替代運動的氣隙的導熱系數(shù)，仿真得到的該工況下穩(wěn)態(tài)溫度場分布如圖10所示。

(a) 徑向的溫度分布

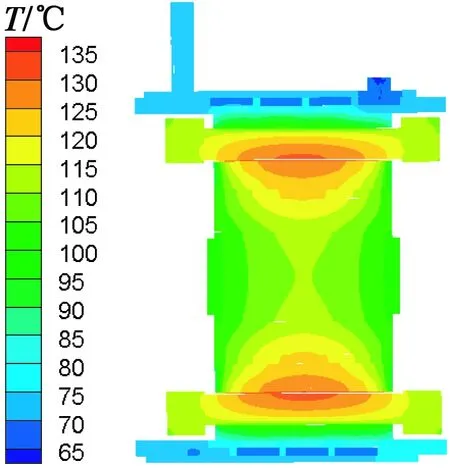
(b) 軸向的溫度分布

由圖10可知，定子齒部的溫度均高于內(nèi)部繞組的溫度，且定子齒部1(具體位置見圖4)的溫度最高，約為135 ℃，實驗測試時該部位的溫度也是最高。由于鐵耗較大，定子齒部的熱流密度很高，導致溫升最大，各個部位溫度的仿真與實驗值如表5所示。從表5中可以看出，誤差穩(wěn)定在11%左右，結果相對可靠。

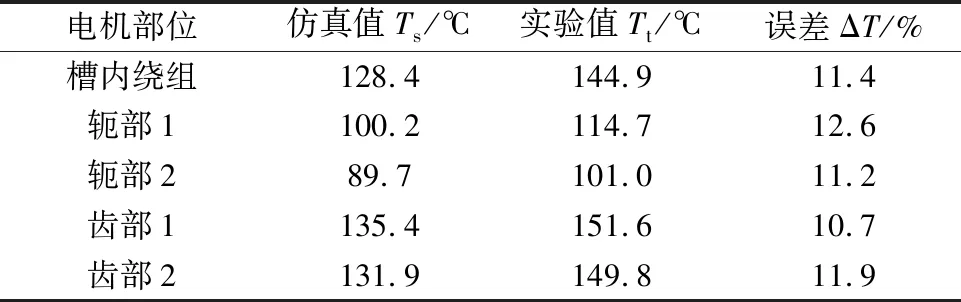
表5 峰值轉速工況下實驗值與仿真值的對比

5 結 論

本文以80 kW永磁同步電機為研究對象，基于有限元法和熱網(wǎng)絡法，采用強迫冷卻方式，針對該電機在不同工況下的溫升特性進行仿真計算和實驗測試，得出如下結論：

1)額定工況下，永磁電機若采用自然冷卻，無強制冷卻時，定子繞組中部的溫度最高，定子鐵心與轉子鐵心的溫度均超過所允許的最大值，永磁體的溫度超過了不可逆退磁溫度，電機無法正常工作，所以必須采用強迫冷卻方式。

2)樣機在強迫水冷方式下，當額定工況下運行達到穩(wěn)態(tài)時，繞組端部的溫升最突出；而在峰值轉速工況下達到穩(wěn)態(tài)時，定子齒部的溫升最大；在峰值轉矩工況下瞬態(tài)運行2 min后，定子槽內(nèi)繞組的溫度最高。在3種工況下，各部分的最高溫度值均在電機絕緣等部件所承受的范圍內(nèi)，即電機可正常運行。

3)采用強迫水冷的永磁同步電機在分析額定工況以及峰值轉矩工況下的溫升特性時，考慮到計算資源與計算時間成本的問題，選用熱網(wǎng)絡法可以快速得到比較可靠的結果；計算峰值轉速工況下電機溫度場分布時，若電機轉速對應的雷諾數(shù)超過臨界雷諾數(shù)，使用有限元法可以得到更加可靠的結果。