數（shǔ）之表象，數（shù）之本質

金妤茜

筆者有幸觀摩江蘇寧雅瑛老師執教“千以內數的認識”寧雅瑛老師的課上設計了大量頗為有趣的操作體驗活動，讓學生在擺數、數數和撥數等過程中操作、觀察、比較和歸納，以形象的“數（shǔ）”聚焦抽象的“數（shù）”，逐步形成數的意識，建立數的概念，理解數的意義，感受數的應用，進而形成數感。

一、不同之“和”

【教學片段1】擺數

師：現在有多少小動物？

生：324。

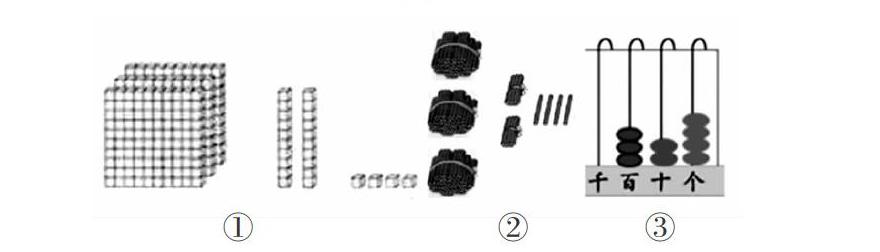
師：324這個數你能用學具盒中的材料表示出來嗎？4人一組，動手擺一擺。

學具盒中有：小棒、計數器、小方塊等。

學生分組操作，全班交流。

生：我是用小方塊擺的，我先擺3個百，2個十，再擺4個一，這就是324。

生：我用小棒來表示的，我也是用了3個百，2個十和4個一。

生：我是用計數器來表示的，我先在百位上撥3粒珠子，十位上撥2粒珠子，最后在個位上撥4粒珠子。

師：同學們用計數器、小棒和小方塊都表示出了324，為什么？

生：因為只要表示出3個百，2個十和4個一，合起來就是324。

小結：明確了有幾個百、幾個十和幾個一，就知道這個數是幾百幾十幾了。

【賞析】在學習“千以內數的認識”之前，學生已經經歷了10以內數的認識、20以內數的認識、百以內數的認識，而且也都有借助計數器、小棒等學具進行輔助學習。本節課上，寧老師選用多種素材請學生通過擺一擺的操作活動表示出324，可謂一舉多得。其一，調動了學生已有的認數經驗，即在不同階段使用的表達數的方式，如小棒、方塊、計數器等，用熟悉的素材來表示新的數，無形中促進了數知識的遷移。其二，小棒、方塊等在表示數的過程中幫助學生再次建立了相應計數單位的表象，比如一捆小棒就表示十，一大捆小棒就表示百等;而計數器不僅幫助學生回顧了已學的計數單位和計數單位之間的十進制關系，并且初步滲透了位值思想。其三，由小棒和方塊再到計數器，不同層次的表征方式持續刺激學生去深刻感悟數的組成，從而達成對數的意義的抽象理解。學生通過自己動手操作，發動多種感官獲取最直接的感覺，然后教師引導學生理性思辨，得出不同的擺法，其實講述著同一個數學道理，即學生口中的“3個百，2個十和4個一，合起來就是324”。

二、變化之“本”

【教學片段2】數數

要求1：一十一十地數，從350數到460。

學生先在計數器上表示出350，然后按要求嘗試。

師：390再加10，是多少呢？

生：十位滿十，向百位進一，變成400。

師生繼續邊撥邊數。

要求2：一個一個地數，從989數到999。

學生先在計數器上表示出989，然后按要求嘗試。

師：一個一個地數，是在哪一位上添珠呢？

生：個位。

師：989，再在個位上添上1顆珠，是多少呢？

生：個位滿十，向十位進一，得到990。

師生繼續邊撥邊數。

要求3：999，如果再添上1顆是多少呢？

師：在計數器上怎樣表示呢？

生：個位滿十向十位進一，十位滿十就向百位進一，百位也滿十了，要再向前一位進一。

師：這時的計數器還夠表示嗎？

生：不夠，要添上一個數位“千”。

師追問：千在哪兒呢？

生：百位的左面，從右往左數第四位。

師：不錯，這就是我們今天要學習的新的計數單位——千。

要求4：學生從表示100的方塊開始，一百一百地數到一千。

要求5：學生看著數軸數，一百一百地數到一千。

（從左往右依次出現）

師追問：學到現在我們認識了哪些計數單位？它們之間有著什么樣的聯系？

生：我們已經認識了個、十、百這些計數單位，今天又認識了新的計數單位——千。

生：10個一是十，10個十是一百，10個百是一千，每個相鄰的計數單位之間的進率是10。

【賞析】數是一個抽象的概念，而“數一數”能讓這種抽象概念以直觀又有序的方式呈現出來，從一個一個地數、一十一十地數，再到一百一百地數，學生的經驗在自然生長，對千以內的數也有了初步感知。對于“千”，學生應該早已接觸，基于生活經驗或是源于課外讀物，但都只是停留在表面的認識。當進行到“數到999，再添上1，是多少”時，學生借助已有的數數經驗和知識結構，自然會產生用新的計數單位表示的需求。這個過程，學生進行的是理性的思考和推理，從而觸摸到了計數單位形成的本質“十進制計數法”。最巧妙的是寧老師并沒有淺嘗輒止，她借助方塊和數軸這兩個數學化的載體讓學生一百一百地數，趁勢突出了10個百是一千，從而讓學生在原有的知識基礎上充分理解計數單位“千”的實際意義。整個環節，教師的追問和提領，幫助學生在感性認知與理性演繹中對“千”的認識從表象走向本質。

三、相同之“質”

【教學片段3】撥數

出示：

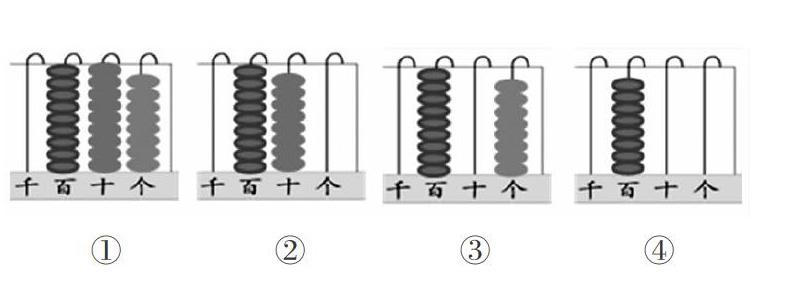
師：仔細觀察，這幾個計數器分別表示的是哪些數？

生：分別是998，980，908和800。

問題1：（指第一個計數器的個位）這8顆珠表示什么？另幾個計數器上的8顆珠又分別表示什么意思？

生：分別表示8個一，8個十和8個百。

師追問：同樣是8顆珠子，怎么表示的含義不一樣？

生：因為珠子所在的位置，也就是數位不一樣，表示的意義也不一樣。珠子的個數和所在的數位都非常重要。

問題2：在哪個計數器上，如果再撥2顆珠就能到1000了？

生：在第4個計數器的百位上再撥2顆珠，就變成了10個百，10個百就是1000。

生：在第1個計數器的個位上再撥2顆珠，滿十進一到十位。十位又滿十，再進一到百位，百位也滿十，再進一到千位，千位上有1顆珠子，就是1000。

生：在第2個計數器的十位上撥2顆珠，十位滿十進一到百位，百位本來就有9顆珠子，所以百位也滿十，再進一到千位，得到1000。

師追問：我們通過在不同數位上再撥2顆珠都得到了1000，要得到1000的關鍵是什么？

生：首先考慮要使百位能滿十進一就能得到1000了。

生：百位上滿十進一得到1000，而其他數位上不能有別的珠子。

小結：撥珠時要思考每個數位上已有的珠子和相鄰計數單位的十進制關系。

【賞析】當學生的記數方法從累數制發展到位值制時，計數器是極好的載體。而位值作用只有在與其他位置產生聯系和區別時才能凸顯。寧老師設計的“讀數撥珠”的活動，形數結合，珠動而數出，指向學生的思維涌動，學生對計數單位和位值思想的認知得到了內化和提升。首先用計數器呈現了4個數，請學生讀數，然后問題聚焦到“同樣是8顆珠子，怎么表示的含義不一樣？”通過類比觀察，學生加深了對計數單位意義的本質認識：同樣的數字在不同的數位上表示的意義不同。接著寧老師拋出挑戰性問題“在哪個計數器上，如果再撥2顆珠就能到1000了？”這是個動手操作與動腦思考并行的數學活動，將對數的本質理解體現得淋漓盡致。其一，“再撥2顆”，2顆撥的數位不同，表示的數值也不同，學生在動手撥之前先進行推理和計算，并且是基于計數單位的計算。如800，再撥2顆珠子，學生思考的是8個百加2個百等于10個百，10個百就是1000。其二，連續的“滿十進一”思維操作，促進了學生對“十進制計數法”的建構。如998，再撥2顆珠在個位，滿十進一到十位，十位又滿十進一到百位，百位也滿十進一到千位，這時千位上有1顆珠，就是1000。如此體驗，學生對滿十進一的認知就不是單一地停留在某一個數位，而是一次完整的經歷和感悟。

（作者單位：江蘇省蘇州工業園區星港學校？搖？搖？搖？搖責任編輯：王彬）